单星无源定位原理及精度分析
龙 宁
(中国西南电子技术研究所,成都 610036)
1 引 言
对未知信号的高精度定位是电子侦察卫星的一项关键技术。与雷达信号的宽带、短时猝发特性相比,通信信号和测控信号的特点是窄带,能进行长时间的连续观测。在实际应用中,通常对通信信号、测控信号都采用与对雷达信号定位相同的方法,从而导致通信信号和测控信号的定位误差很大(几十公里),不能满足战略监视和战术支援需要的几公里定位精度要求。
在单星平台中,能实现对地面辐射源定位的方法很多。测向定位法可以实现瞬时定位,但由于采用干涉仪测向,需要解相位模糊,天线结构复杂,并且由于受测向精度的限制,定位误差为几十公里[1—2];文献[3]提出了一种通过测脉冲到达时间实现对地表静止辐射源无源定位的方法,适用于对具有固定PRF的雷达信号定位,而雷达信号的复杂多样性决定了这种方法不能用于实际战场环境中;文献[4]提出了一种基于最小二乘准则,使相位误差最小化的无源定位方法,该方法特别适用于对短时猝发信号的定位,定位精度优于测向定位法,可以达到十公里左右,但由于需要二维干涉仪,对于Ku、Ka频段及以上信号的定位,容易产生定位模糊点,并且天线结构复杂;文献[5]提出了一种测频测相位差无源定位方法,定位精度较单一的利用频率和相位差定位方法精度更高,可以达到几公里,但需要多次测量信号频率,适用于对持续时间长的通信信号定位,同相位差定位法一样,由于需要二维干涉仪,对于Ku、Ka频段及以上信号的定位,容易产生定位模糊点,并且天线结构复杂。测频定位法是利用观测平台和目标之间相对运动所产生的多普勒频率对辐射源进行定位,并且信号频率越高,定位精度越高,由于只有一个模糊点,易解定位模糊;另一个显著优点是仅需要单天线,天线结构简单,成本低,可靠性高[6—10]。
综上所述,由于低轨卫星运动速度快,信号的多普勒频率大,而且信号带宽越窄测频精度越高,定位精度也越高,因此,利用测信号多普勒频率定位的方法特别适用于对持续时间长、信号带宽窄的通信信号和测控信号进行高精度定位。
本文首先分析了通信信号和测控信号目前工程可实现的测频精度,然后论证了在单星平台上利用测频定位技术实现通信、测控信号高精度定位的可行性,最后根据5 km定位精度要求提出了对信号持续时间、信号载频、频率测量误差及卫星轨道高度的要求。
2 多普勒定位技术实现通信、测控信号高精度定位的可行性分析
在卫星通信中,通过对地面辐射源辐射的信号进行测频,得到信号的多普勒频率观测量,利用信号的多普勒频率与辐射源距离成正比的关系,建立多个距离曲面,可完成对未知辐射源的定位。
在地固坐标系中,假设待测辐射源的坐标P=[x y z](单位:m),连续n次频率测量时的卫星的坐标为Mi=[MxiMyiMzi](单位:m),i=1,2,…,n,卫星速度 VMi=[VMxiVMyiVMzi](单位:m/s),i=1,2,…,n,如图 1所示。

图1 测频定位示意图Fig.1 Illustration of frequency localization
定位方程可描述为

其中:
fi为第i次接收地面辐射源发射信号频率的测量值(单位:Hz),ri是卫星到辐射源的距离(单位:m),i=1,2,…,n;fc为地面辐射源发射信号的载频(未知)(单位:Hz),c为光速(单位:m/s);
最后一个方程是地球面参考模型方程,a为地球长轴(单位:m),e2为地球第一偏心率的平方。
根据式(1)可以求解出辐射源的位置,单星测频定位存在模糊解,在卫星轨迹线的两边各有一个解,通过比幅法即可以解定位模糊。
测量n次信号频率可以得到n+1个方程,对于地球面的辐射源,通过卫星平台对同一地面目标进行3次频率测量就可确定辐射源的位置。由于定位方程是一个非线性方程组,利用解析法求解较困难。利用泰勒级数展开将定位方程线性化后可以进行迭代求解目标位置,也可以利用数值搜索法直接得到定位结果。该定位方程有两个定位结果,并且在卫星轨迹线的两边各有一个解,其中一个是辐射源真实位置的估计值,通过比幅法即可以判定出辐射源在卫星轨迹线的哪一侧。
从式(1)中可以看出,测频定位方法的定位精度取决于频率测量精度。由于信号带宽越窄,频率测量精度越高,因此,测频定位方法特别适用于对测控信号、通信信号等窄带信号进行定位。假设采样频率选为3倍信号带宽,如果做8192点DFT测信号频率,则频率的均方根测量误差为是采样频率,N是DFT点数。
经计算,做8192点DFT时,不同信号带宽可获得的频率均方根测量误差见表1。
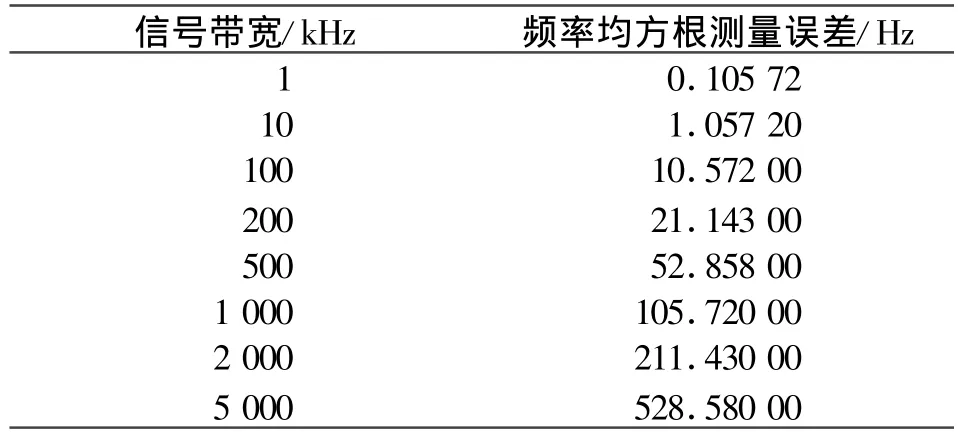
表1 不同信号带宽的频率均方根测量误差Table 1 Frequency RMS measurement error of different signal bandwidth
从表1中可见,在信号带宽2 MHz以内时,信号频率测量精度可以达到200Hz左右,带宽越窄,频率测量精度越高,越有利于定位。如果采用更高点数的DFT,则可以获得更高的测频精度。目前,在工程中业界已经大量采用FPGA器件实现8192、16284甚至更多点数的FFT。
由于在实际应用中的绝大部分通信信号和测控信号的带宽都在2 MHz以内,测频精度可以达到100Hz以内,由此可见,利用测频定位方法实现对通信信号和测控信号的高精度定位是可行的。在下一节中将进一步计算实现定位精度5 km时对测频精度的要求。
3 通信、测控信号高精度定位对信号特征及平台的要求
在卫星平台上利用测频定位方法实现对通信信号和测控信号的高精度定位对信号特征的要求体现在信号持续时间、信号载频、频率测量误差3个方面;对卫星平台的要求体现在轨道高度上,对卫星的姿态没有要求。下面根据通信信号和测控信号的定位精度达到5 km的要求,分析对信号特征及平台参数的指标要求。
3.1 对信号持续时间的要求
假定卫星高度700km,载频6GHz,频率测量误差为50Hz,采样间隔1 s,经计算,如果要求达到5 km的定位精度,要求信号持续时间不低于30s,见图2。

图2 信号持续时间30s时的圆概率定位误差分布Fig.2 Circular probability orientation error distribution in 30s signal duration
3.2 对载频的要求
假定卫星高度700km,频率测量误差为50Hz,信号持续时间30s,采样间隔0.1 s,经计算,如果要求达到5 km的定位精度,要求载频1GHz以上,见图3。

图3 载频1 GHz时的圆概率定位误差分布Fig.3 Circular probability orientation error distribution at 1GHz carrier frequency
3.3 对频率测量误差的要求
假定卫星高度700km,载频4 GHz,信号持续时间50s,采样间隔1 s,经计算,如果要求达到5 km的定位精度,要求频率测量误差优于100Hz,见图4。
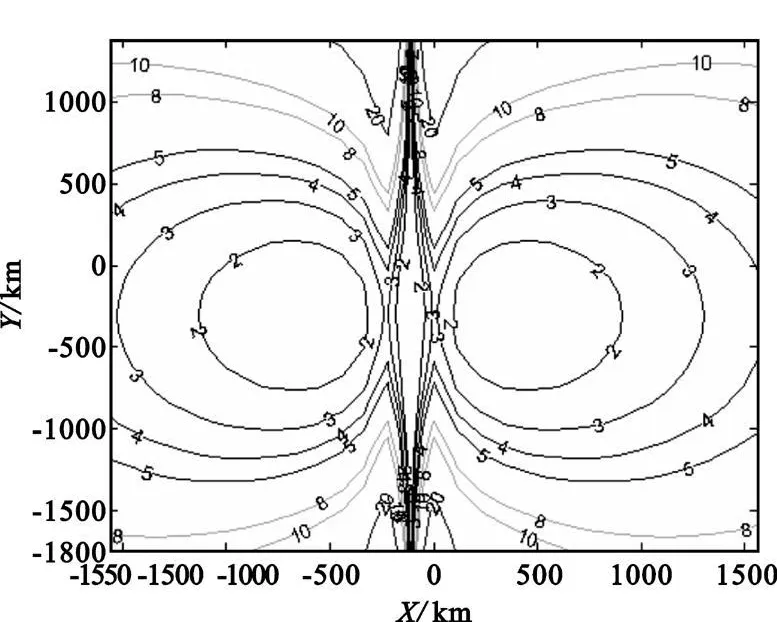
图4 频率测量误差100Hz时的圆概率定位误差分布Fig.4 Circular probability orientation error distribution at 100Hz frequency measurement error
3.4 对卫星轨道高度的要求
假定载频3GHz,频率测量误差为100Hz,信号持续时间50s,采样间隔1 s,经计算,如果要求达到5 km的定位精度,要求卫星轨道高度不高于800km,见图 5。

图5 卫星高度800km时的圆概率定位误差分布Fig.5 Circular probability orientation error distribution at 800km satellite orbit
综上所述,在卫星轨道高度800km以内时,在L频段及以上,频率测量误差小于100Hz时,只需要有30~50s左右的信号持续时间,就可以达到5 km的定位精度。
4 结束语
研究结果表明:在星载平台上利用测频定位法对通信、测控信号进行定位,可以达到5 km的定位精度,远远优于传统的基于测向定位法几十公里的定位精度,并且具有天线结构简单、易解定位模糊的优点,为该技术工程应用时的指标设计提供了依据。由于信号持续时间越长,采样次数越多,定位高精度越高,但解定位方程的计算量也越大,因此,高效的定位方程求解算法是我们下一步的研究内容。
实现通信、测控信号高精度定位的方法很多,本文只是针对具体应用提出了一种方法,欢迎同行、专家批评指正。
[1]袁孝康.相位干涉仪测向定位研究[J].上海航天,1999(3):1-7.YUAN Xiao-kang.Study on Direction Finding and Position with Phase Interferometers[J].Aerospace Shanghai,1999(3):1-7.(in Chinese)
[2]龚文斌,谢恺,冯道旺,等.星载无源定位系统测向定位方法及精度分析[J].长沙电力学院学报(自然科学版),2004,19(2):64-67.GONG Wen-bin,XIE Kai,FENG Dao-wang,et al.Method&Precision Analysis of Direction-finding and Position Based on Satellites Passive Location System[J].Journal of Electric Power Science and Technology,2004,19(2):64-67.(in Chinese)
[3]徐义,郭福成,冯道旺.一种单星仅测TOA无源定位方法[J].宇航学报,2010,31(2):502-507.XU Yi,GUO Fu-cheng,FENG Dao-wang.A New Satellite Passive Localization Method Using TOA Measurement Only[J].Journal of Astronautics,2010,31(2):502-507.(in Chinese)
[4]陆安南,杨小牛.最小相位误差单星无源定位法[J].上海航天,2007,(3):6-9.LU An-nan,YANG Xiao-niu.Passive Location with Minimizing Phase Difference Error by Single Satellite[J].Aerospace Shanghai,2007,24(3):6-9.(in Chinese)
[5]陆安南,杨小牛.单星测频测相位差无源定位[J].系统工程与电子技术,2010,32(2):244-247.LU An-nan,YANG Xiao-niu.Passive location from the combined set of frequency and phase difference measurements by single satellite[J].System Engineering and Electronics,2010,32(2):244-247.(in Chinese)
[6]Chan Y T,Towers J J.Passive localization from Doppler shifted frequency measurements[J].IEEE Transactions on Signal Processing,1992,40(10):2594-2598.
[7]Fowler M L.Analysis of single-platform passive emitter location with terrain data[J].IEEE Transactions on Aerospace and Electronics Systems,2001,37(2):495-507.
[8]Wu N E,Fowler M L.Aperture error mitigation via localstate estimation for frequency-based emitter location[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(2):414-429.
[9]陆安南,孔祥正.单星测频无源定位法[J].通信学报,2004,25(9):160-168.LU An-nan,KONG Xiang-zheng.Passive localization from frequency measurements by single satellite[J].Journal on Communications,2004,25(9):160-168.(in Chinese)
[10]李杨,周彬.基于概率的单星测频无源定位算法[J].电子信息对抗技术,2007,27(3):7-10.LI Yang,ZHOU Bin.Passive Location Algorithm by Frequency Measurements of Single Satellite Based on Probability[J].Electronic Information Warfare Technology,2007,27(3):7-10.(in Chinese)

