破片模拟弹侵彻陶瓷 ／船用钢复合靶板的理论分析模型研究

赵留平

中国舰船研究设计中心军事代表室，湖北武汉 430064

破片模拟弹侵彻陶瓷 ／船用钢复合靶板的理论分析模型研究

赵留平

中国舰船研究设计中心军事代表室，湖北武汉 430064

简要回顾了陶瓷／金属复合靶板的研究现状。根据船用钢的吸能特点和船用陶瓷轻型复合装甲的特殊性，将10 g破片模拟弹侵彻陶瓷／船用钢的过程分为两个阶段，分别计算了破片模拟弹的侵蚀变形能和船用钢背板的隆起—碟型变形吸能，并将后者分为径向弯曲变形能、径向膜拉伸变形能及周向弯曲变形能等，给出了各种能量的计算公式，建立了计算弹道极限的理论分析模型，其结果与实验吻合较好。结果表明，陶瓷／船用钢的耗能机制主要是弹体的侵蚀变形能和船用钢背板的变形能。

穿甲力学；陶瓷装甲；高速冲击；破片模拟弹；理论模型

1 引言

陶瓷材料因具有高抗压强度和低密度的特性而被越来越广泛地应用于防弹领域，如飞机、舰船、坦克装甲车辆等的弹道防护，可大幅减轻装甲防护系统的重量。目前，陶瓷复合装甲的形式主要是以陶瓷为迎弹面板，具有良好韧性的金属做背板。其利用陶瓷的高硬度、高强度、高弹性模量来钝化、侵蚀、碎裂弹体，传递冲击载荷，增大背板的吸能范围，从而满足抗侵彻能力的要求；利用金属背板的韧性及延展性吸收大量的弹体动能，从而满足抗冲击能力和抗崩落能力的要求。可见，弹体对陶瓷／金属复合靶板的侵彻研究具有重要意义。但侵彻的过程依赖多种因素，使得这一问题的研究显得复杂又困难。

弹体侵彻陶瓷／金属复合靶板的机理复杂，但工程简化分析模型却可以快捷地获得复合靶板的抗弹性能参数。早期的工程简化分析模型主要是Florence模型，但当陶瓷面板厚度小于弹体直径或金属背板较薄时，其误差较大［1］。近年来，不少学者根据各自不同的研究对象建立了分析模型，如Goncalves等［2］建立了一维陶瓷／金属靶板抗侵彻模型，利用应变能密度计算了金属背板的塑性变形功；Zaera等［3］在考虑背板动能的基础上研究了背板的吸能；杜忠华等［4］假设金属背板为薄板的动力响应模型，结合能量法建立了陶瓷／金属复合靶板抵抗小型穿甲弹侵彻的理论分析模型；张晓晴等［5］将弹体的镦粗变形、陶瓷面板碎裂及陶瓷锥的形成变化与金属背板的变形结合起来，建立了可变形弹体垂直侵彻陶瓷／金属靶板理论分析模型；申志强等［6］将金属背板的变形和穿孔模式等同于爆炸冲击载荷作用下金属薄板的变形和破口模式，并在此基础上建立了弹道极限工程分析模型。这些工程简化分析模型都考虑了弹体的质量和速度损失，却忽略了弹体的侵蚀变形能和陶瓷的破碎吸能。有研究表明，这两项的耗能可达初始动能的55%～85%［7］，而弹体的侵蚀变形能就占初始动能的20%～40%。陶瓷／船用钢复合靶板与一般的轻型陶瓷复合装甲不同，例如，坦克用陶瓷装甲的厚度比（陶瓷面板／装甲钢背板）为4∶3，而船用轻型陶瓷复合装甲的陶瓷厚度与船用钢背板的厚度比为1.0左右；船用钢背板具有良好的韧性和延展性，其是通过产生较大的塑性变形来吸收陶瓷锥和弹体的动能，而装甲钢则是通过其高硬度和高强度来消耗弹体的动能。普通的陶瓷复合装甲与船用陶瓷复合装甲因有这两方面的不同，使得一般的工程简化分析模型在研究高速破片模拟弹侵彻陶瓷／船用钢复合靶板的弹道极限时遇到了一定的困难，无法进行合理的预测。

基于以上研究背景，本文以10 g高速破片模拟弹侵彻陶瓷／船用钢复合装甲的弹道极限为研究对象，结合陶瓷和船用钢的变形和吸能特征，考虑破片模拟弹的侵蚀变形能和因破碎磨损而产生的质量损失，以及船用钢背板的隆起—碟型变形吸能，应用能量法建立了理论分析模型，并通过弹道实验进行了验证。

2 理论分析模型的建立

2.1 模型建立依据

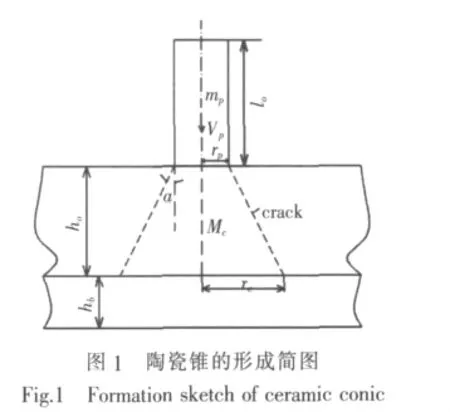
破片模拟弹以一定的初速度侵彻陶瓷／船用钢复合靶板，根据陶瓷复合靶板的变形吸能特征和破片模拟弹的侵彻机理，将其侵彻过程简化为两个阶段：破片模拟弹与陶瓷面板的作用以及破片模拟弹与陶瓷变形锥形成的组合弹体对船用钢背板的作用。在第1个侵彻阶段中，由于陶瓷具有极高的硬度和强度，根据修正的Tatés流体动力模型，破片模拟弹将会发生侵蚀，质量会发生损失，动能减小，同时，在破片模拟弹的作用下，陶瓷面板会沿其厚度方向形成一个变形陶瓷锥。在陶瓷锥形成后（图1），进入第2个侵彻阶段，破片模拟弹与陶瓷锥形成的组合弹体将共同作用于船用钢背板，船用钢在组合弹体的共同作用下将出现较大范围的隆起—碟型变形、鼓包，直至穿孔。根据以上侵彻过程分析，可见弹体的质量损失主要发生在第1阶段，而陶瓷破碎锥也在该阶段形成，因此，破片模拟弹的质量损失与陶瓷破碎锥的形成是经历了相同的时间。在破片模拟弹的侵彻过程中，船用钢背板的隆起—碟型变形吸能是主要的吸能机理。

2.2 破片模拟弹的侵蚀变形能分析

由于反舰导弹战斗部爆炸产生的高速破片的形状一般具有不规则性（预制破片除外），根据穿甲力学的理论知识，不同形状的破片，其侵彻机理和侵彻能力存在较大差异，这将对舰船装甲防护结构设计及其抗弹性能评估带来许多难以确定的因素。近年来，西方国家在弹道冲击研究中大量使用破片模拟弹 （Fragment Simulating Projectile，FSP），主要有北约国家和美国针对破片杀伤穿甲特点而设计的FSP Stanag 2920，如图2所示。其弹体为圆柱体，头部两侧有两个钝切削面，中间为平面凸缘，为美国防部颁发的军事标准MILSTD－662F和美司法部颁布的警用人体装甲弹道标准NIJ－0101.04所采用。因此，本文将10 g FSP作为船用陶瓷复合装甲的主要防护对象。

破片模拟弹的侵蚀时间和陶瓷锥的形成时间tc取决于径向裂纹的传播和横向压缩波的传播，且前者在压缩波传播至陶瓷背面后才开始传播［3］，因此，陶瓷锥的形成时间可表示为：

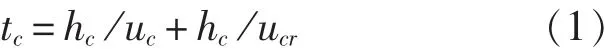
式中，uc为陶瓷的纵向弹性压缩波速，uc=（Ec／ρc）0.5，ρc、Ec分别为陶瓷的密度和弹性模量；ucr为陶瓷的径向裂纹传播速度，其最大值为陶瓷的瑞利波速。

Senf和 Strassburger等［8－9］研究了陶瓷中的动态裂纹传播速度，指出ucr=1／3～1／6uc，而Wilkins［10］和 Reijer［11］则认为采用ucr=1／5uc可以较好地对陶瓷锥的形成进行预测。因此，本文将按照Wilkins和Reijer提出的裂纹传播速度来计算陶瓷锥的形成时间，tc=6hc／uc。

根据Tate－Alekseevskii模型，当弹、靶接触面的压力高于弹丸比拟磨蚀杆的动屈服强度时，弹头进入接触面的部分在高压下呈流体状而被磨蚀，其余部分则近似为刚体，弹体质量的变化方程可近似表示为：

式中，ρp、Ap分别为弹体的密度和截面积。

由于陶瓷锥的形成时间很短，在陶瓷锥形成时，弹体的质量损失Δmp可近似表示为：

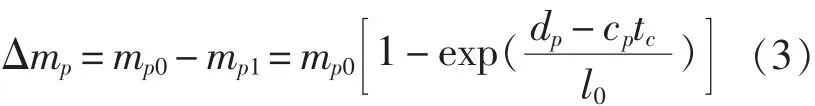
式中，mp0、l0分别为弹体的初始质量和长度；dp为弹体直径；cp为弹体中的塑性波速；mp1为弹体侵蚀后的质量。

假设弹体侵蚀后的体积不再发生变化，弹体的侵蚀体积为ΔV，则弹体的侵蚀变形能Ee为：

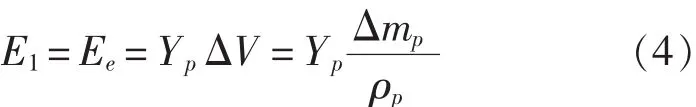
式中，Yp为弹体材料的动态屈服强度。

2.3 陶瓷锥的形成耗能分析

陶瓷锥的形成如图1所示。有文献指出［12］，当弹体速度在220～1 000 m／s间变化时，陶瓷锥的半锥角α在34°～68°之间变化；当弹体速度超过1 000 m／s时，破碎陶瓷的半锥角为68°。结合本文的研究对象，将陶瓷锥的半锥角α取为65°，假定陶瓷锥锥顶直径等于弹体直径，变形锥底部的半径rc=rp+hctgα，则陶瓷锥的质量mc为：

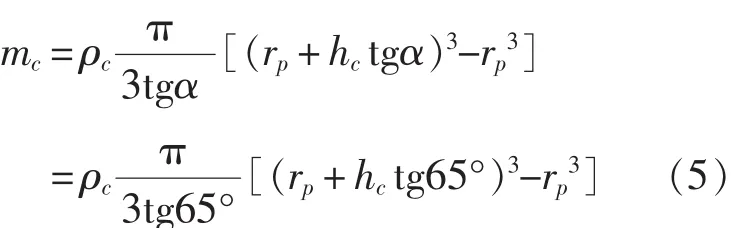
式中，hc表示陶瓷厚度，rp为弹体半径。

Woodward等人［13］的研究表明，陶瓷碎裂破坏形成新的表面所吸收的能量只占弹体动能的很小一部分，约0.2%，完全可以忽略（即忽略陶瓷锥的形成耗能）。陶瓷锥形成后，弹体就与陶瓷锥共同作用于背板，陶瓷锥的作用只是增加了背板的变形区域。

2.4 船用钢背板的隆起—碟型变形耗能

有关弹道试验的结果表明，船用钢背板在未被破片穿透时，将出现隆起—碟型变形，如图3所示。当弹速小于弹道极限时，船用钢背板呈现隆起—碟型变形，其变形能主要包括径向弯曲变形能Erb、径向膜拉伸变形能Erm及周向弯曲变形能Eθb，即背板的变形吸能E2为：

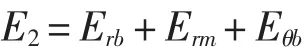
假设船用钢背板的变形为轴对称变形，且只发生法向位移，位移函数w仅是距侵彻点r的函数，则船用钢背板的径向弯曲变形能Erb、径向膜拉伸变形能Erm及周向弯曲变形能Eθb分别为：

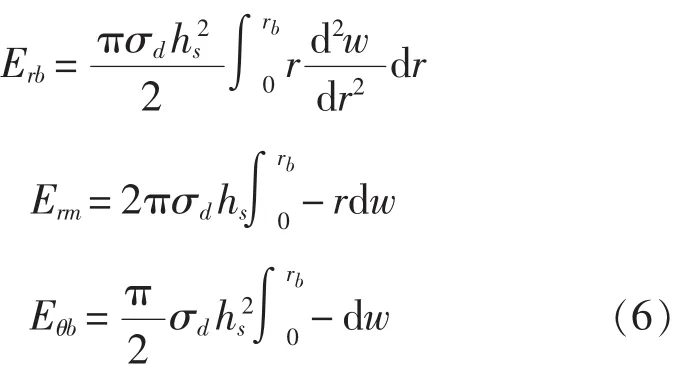
动屈服应力σd可以按照Cowper－Symonds模型进行计算，其中的常数按照低碳钢常用的D=40.4 s－1，n=5取值：

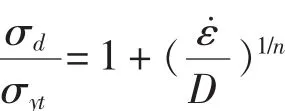
其中，σyt为船用钢的静态屈服强度；ε˙为等效塑性应变率，根据本文的弹体速度，可以将其近似取为1 000 s－1。

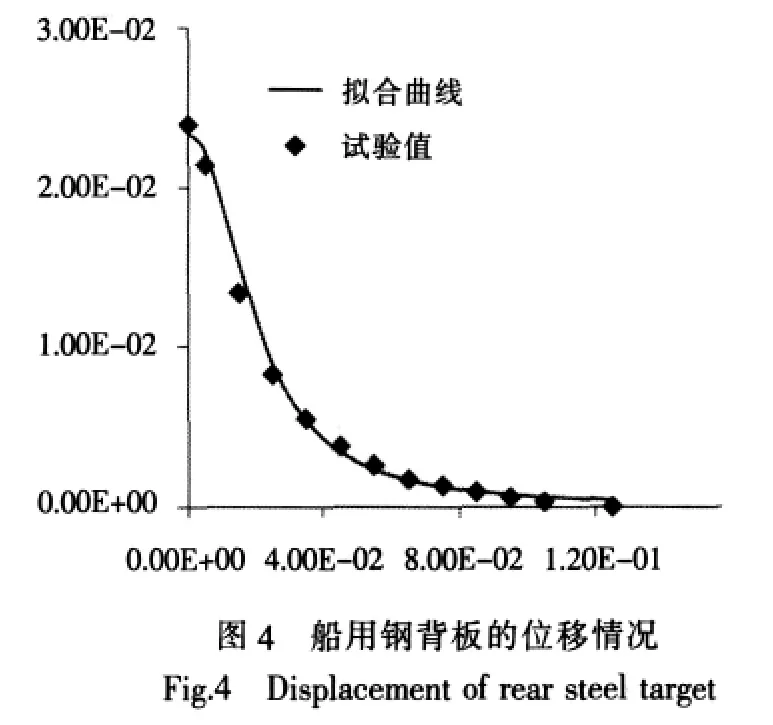
通过对船用钢背板变形情况的测量，可以得到距离侵彻区域不同半径处的位移情况，将这些数据点绘制于图形中，并采用有关曲线进行拟合，在得到船用钢背板的位移函数后，就可以利用式（6）计算有关吸能。图4给出了试验测量所得的船用钢背板有关质点的位移值，结合文献［14］中关于船用钢背板的隆起—碟型变形特征，并拟合本文得到的位移值，假设船用钢背板的位移函数w可表示为：

式中，w0为背板中心的最大挠度，考虑到背板的变形和穿孔模式与爆炸冲击荷载作用下金属薄板的变形和破口模式相似，w0可取为爆炸冲击载荷作用下金属薄板不发生穿孔的最大挠度［15］：w0＝2.47rcεb0.5（εb为背板材料的失效应变；rc为陶瓷锥的底部半径，按rc＝rp＋hctgα计算）；rb为背板发生变形的最大半径。

将式（7）代入式（6），经过积分，可以分别得到Erb、Erm及Eθb的计算式，可以得到船用钢背板的变形吸能E2：

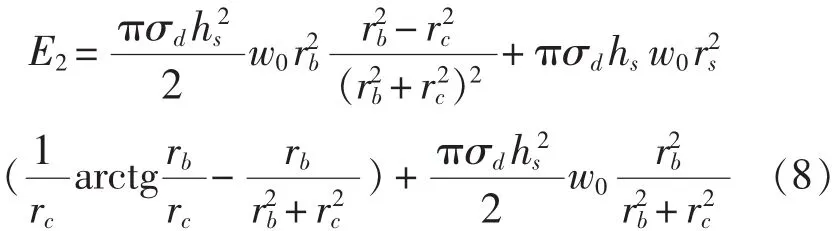
2.5 弹道极限计算

根据以上关于弹、靶系统的耗能分析，可以得到整个侵彻过程中弹体总的动能损失Ea：

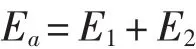
为求弹体侵彻陶瓷／船用钢的弹道极限速度vbl，弹体的初始动能等于以上三个阶段的弹、靶系统的耗能，利用能量守恒，可以得到：

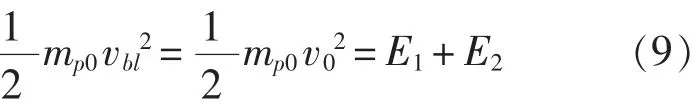
根据E1、E2的表达式，并将其代入式（4），可以得到破片模拟弹侵彻陶瓷／船用钢复合靶板的弹道极限速度计算式。为了比较本文提出的计算模型与国际上较为通用的、经典的Florence模型计算结果间的差异，式（10）给出了Florence模型的计算方程：

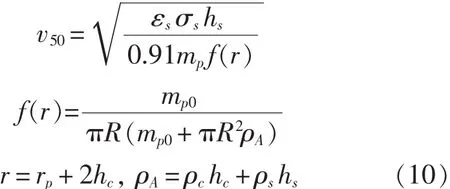
式中，r为陶瓷破碎锥的底部半径，m；rp为弹体半径，m；mp0为弹体质量，kg；ρA为靶板的面密度，kg／m3；hc、hs分别为面板和背板的厚度，m；ρc、ρs分别为面板和背板的密度，kg／m3；εs、σs分别为背板的失效应变和极限拉伸强度，Pa。

3 比较与讨论

3.1 弹道实验设计

为验证本文所提模型的合理性和适用性，对10 g破片模拟弹侵彻船用钢／陶瓷复合装甲的情况进行了弹道实验研究。弹体材料为45号钢（力学性能见表1），淬火处理，其中ν为材料的泊松比，σy、σd分别为材料的静态和动态屈服强度，δs为材料的失效应变。面板选用目前应用较广的装甲陶瓷（99.5%的Al2O3），背板采用普通的船用结构钢Q235钢，厚度hs为船用结构钢的常用厚度；弹体正侵彻。陶瓷面板及船用钢背板和弹体的材料力学性能参数如表1所示。分别对4 mm陶瓷／4 mm船用钢、4 mm陶瓷／6 mm船用钢、4 mm陶瓷／8 mm船用钢、6 mm陶瓷／6 mm船用钢、6 mm陶瓷／8 mm船用钢、6 mm陶瓷／10 mm船用钢、8 mm陶瓷／8 mm船用钢和8 mm陶瓷／10 mm船用钢进行了弹道实验，得到了不同靶板结构下的弹道极限vbl。

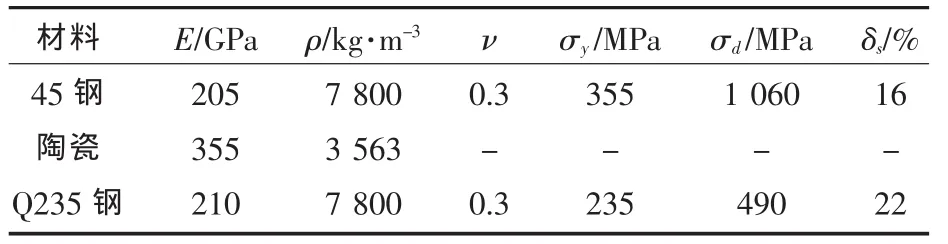
表1 Al2O3陶瓷／船用钢靶板及弹体材料的力学性能Tab.1 Mechanical property of target and FSP

3.2 理论值与试验值的比较

为了比较本文的解析模型与试验结果和经典计算公式的计算结果，引入了计算陶瓷／金属复合靶板弹道极限的经典解析公式Florence模型：

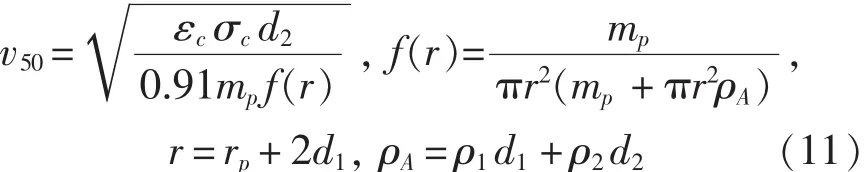
式中，r为陶瓷破碎锥的底部半径，m；rp为弹体半径，m；mp为弹体质量，kg；ρA为靶板的面密度，kg／m3；d1、d2分别为面板和背板的厚度，m；ρ1、ρ2分别为面板和背板的密度，kg／m3；εc、σc分别为背板的失效应变和极限拉伸强度，Pa。

根据本文提出的计算模型，并结合表1给出的弹体、陶瓷和船用Q235钢的材料参数，利用式（4）对弹道实验中使用到的靶板结构进行了弹道极限的预测和计算，弹道实验中所得到的弹道极限值和用本文计算模型所得到的值均列于表2，另表中还给出了Florence模型的计算结果。

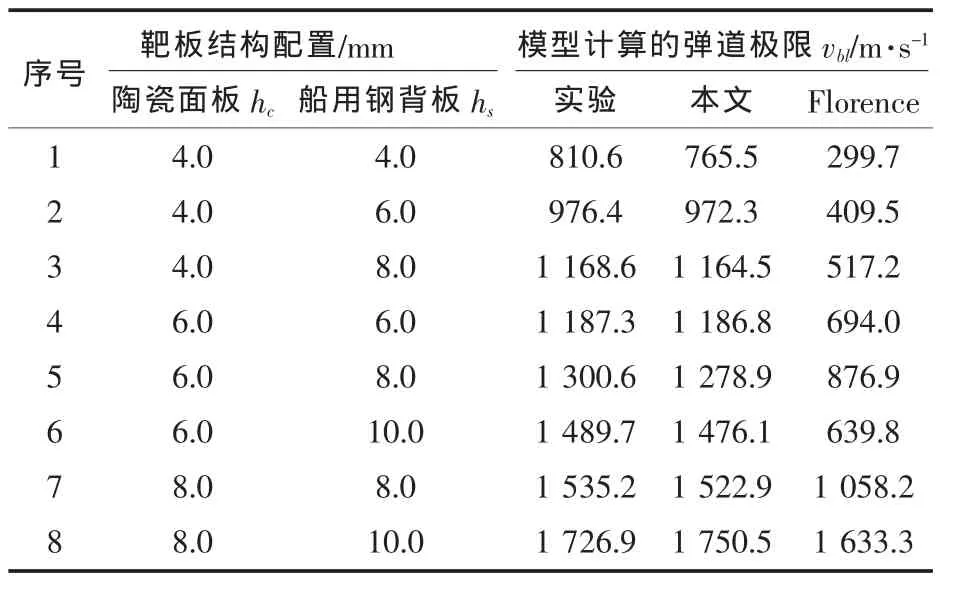
表2 理论计算与试验结果的比较Tab.2 Ballistic limit velocities comparison between theory and experiment

从表2中的有关数据可以看到：

1）本文所提模型与弹道实验的比较：对于破片模拟弹侵彻陶瓷／船用钢复合靶板，弹道极限的试验值与本文所提模型的计算值的误差在6%以内，满足工程需要。可将本文所提模型用于计算陶瓷／船用钢复合靶板的弹道极限速度的主要原因，是本文所提变形吸能模式及背板的位移函数与研究对象的实际变形较为接近，更加可靠。

2）Florence模型与弹道实验的比较：实验的弹道极限值与理论值的误差较大，最大误差为63.03%，但随着陶瓷面板厚度的增加，误差逐渐减小。造成这种现象的主要原因是，Florence模型仅考虑了背板的拉伸变形能而没有考虑背板的其它变形吸能。在陶瓷面板较薄时，如实验1～3，因弹体的侵蚀吸能和背板的弯曲变形能不可忽略，便导致Florence模型的误差较大；但当陶瓷面板较厚时，如实验4～8，背板的拉伸变形能占主要地位，其它两类吸能可忽略，致使Florence模型的误差随陶瓷面板厚度的增加而减小。

3）本文的模型较Florence模型的计算结果更接近于实值。这是因为Florence模型未考虑弹体的质量损失，背板采用的均布质量圆形塑性薄膜振动解与背板的实际变形和破坏模式不符，从而导致计算结果误差较大。而本文的模型则考虑了破片模拟弹在侵彻过程中的质量损失，其采用爆炸冲击载荷作用下金属薄板的运动变形规律来描述背板的力学响应，且考虑了背板的径向弯曲变形能、径向膜拉伸变形能及周向弯曲变形能，因而取得了与实验值更为接近的计算结果。

本文提出的计算模型能较好地对陶瓷／船用钢的弹道极限进行预测，而经典的Florence模型则存在较大的计算误差，只是随着陶瓷厚度的增加，其计算值与实验值之间的误差会逐渐减小。

4 结论

经过本文的研究，可以得到以下结论：

1）本文将10 g破片模拟弹侵彻陶瓷／船用钢的耗能分为弹体的侵蚀变形能和隆起—碟型变形耗能（包括径向弯曲变形能、径向膜拉伸变形能及周向弯曲变形能），建立了各种形式耗能的计算公式，并根据能量守恒原理，得到了弹道极限的理论分析模型。

2）对典型的陶瓷／船用钢复合靶板进行了弹道实验研究，并将实验结果与本文的理论分析模型和Florence模型进行了对比，结果表明，本文模型的计算值与实验值吻合较好，Florence模型的误差是随陶瓷面板厚度的增加而减小。

［1］ 蒋志刚，谭清华，曾首义，等.陶瓷／金属复合靶板优化设计［J］.弹道学报，2006，18（2）：69－71，74.

［2］ GONCALVES D P，DE MELO F C L，KLEIN A N，et al.Analysis and Investigation of Ballistic Impact on Ceramic／Metal Composite Armour［J］.International Journal of Machine Tools＆Manufacture，2000，44（2－3）：307－316.

［3］ ZAERA R，SÁNCNEZ－SÁEZ S，PÉREZ－CASTELLANOS J L，et al.Modelling of the adhesive layer in mixed ceramic／metal armours subjected to impact［J］.Composites，Part A：applied science and manufacturing，2000，31（8）：823－833.

［4］ 杜忠华，赵国志，杨大峰，等.弹丸垂直侵彻陶瓷／金属复合靶板的简化模型［J］.弹道学报，2001，13（2）：13－17.

［5］ 张晓晴，杨桂通，黄小清.弹体侵彻陶瓷／金属复合靶板问题的研究［J］.工程力学，2006，23（4）：155－159.

［6］ 申志强，蒋志刚，曾首义.陶瓷金属复合靶板工程模型及耗能分析［J］.工程力学，2008，25（9）：229－234.

［7］ Anderson C E，James D.An analytical model for dwell and interface defeat［J］.International Journal of Impact Engineering，2005，31（9）：1119－1132.

［8］ SENF H，STRASSBURGER E，ROTHENHÄUSLER H.Stress wave induced damage and fracture in impacted glasses［J］.Journal De Physique IV，1994，4（3）：741－746.

［9］ STRASSBURGER E，SENF H，ROTHENHÄUSLER H.Fracture propagation during impact in three types of ceramics［J］.Journal De Physique IV，1994（3）：653－658.

［10］ WILKINS M L.Mechanics of penetration and perforation［J］.International Journal of Engineering Science，1978，16（11）：793－807.

［11］ REIJER D.Penetration of 7.62 AP projectiles into ceramic faced armour［C］//Proc.on the 11th International Symposium on Ballistics.Belgium：Brussels Congress Centre，1989，（Ⅲ）：77－85.

［12］ 杜忠华，赵国志，杨玉林.陶瓷／玻璃纤维／钢板复合靶板抗弹性能的研究 ［J］.兵工学报，2003，24（2）：219－221.

［13］ WOODWARD R L，GOOCH W A，O＇Donnell R G，et al.A study of fragmentation in the ballistic impact of ceramics［J］.International journal of impact engineering，1994，15（5）：605－618.

［14］ 侯海量.大型舰船水上舷侧结构抗毁伤机理研究［D］.武汉：海军工程大学，2006.

［15］ WIERZBICKI T.Petalling of plates under explosive and impact loading［J］.International Journal of Impact Engineering，1999，22（9/10）：935－954.

Analytical Modeling of Fragment Simulating Projectile Penetrating Mixed Ceramic/Steel Armor

Zhao Liu－ping
Military Representative Office in China Ship Development and Research Center，Wuhan 430064，China

Research development of ceramic／steel composite armor is reviewed.The process of 10g fragment simulating projectile（FSP）penetrating ceramic light－duty composite armor is divided into two phases，according to the absorption energy characteristics of ship steel and particularity of ceramic lightduty composite armor.Erosion deformation energy of FSP and hunch－dishing deformation of ship building steel are calculated.The hunch－dishing deformation absorption energy of ship building steel is divided into three parts：radial bending deformation energy，radial membrane stretching deformation energy and circumferential bending deformation energy.The calculating formulas of absorption energy are presented.The analytical model of ballistic limit velocity is built.The analytical results accord with experimental values，and also indicate that the erosion deformation energy of FSP and hunch－dishing deformation of ship building steel are the leading consumption energy mechanism.

mechanics of perforation；ceramic armor；high velocity impact；fragment simulating projectile；analytical model

U661.43

A

1673－3185（2011）02－40－06

10.3969/j.issn.1673-3185.2011.02.008

2010-10-12

箱形梁结构的应用可行性研究（09J1.3.2）

赵留平（1969－），男，硕士，工程师。研究方向：舰船总体设计。E-mail：wxq11211＠163.com