基于排队论的大型舰船甲板弹射器数量研究

周鑫磊 孟祥印 解学参 胡玉龙 侯远杭

1海军装备部沈阳局，辽宁 沈 阳 110031

2哈尔滨工程大学 船舶工程学院，黑龙江 哈 尔滨 150001

3中国舰船研究设计中心，湖北 武 汉 430064

基于排队论的大型舰船甲板弹射器数量研究

周鑫磊1孟祥印2解学参3胡玉龙2侯远杭2

1海军装备部沈阳局，辽宁 沈 阳 110031

2哈尔滨工程大学 船舶工程学院，黑龙江 哈 尔滨 150001

3中国舰船研究设计中心，湖北 武 汉 430064

为明确大型舰船飞行甲板弹射器数量设计的理论依据，从调运指挥官的角度提出了“虚拟队列”概念，分析了其工作特点，对其工作模式进行了排队论建模。同时分析、建立了舰载机在弹射等待过程中的真实排队模型。忽略其它甲板因素的影响，基于排队论假设代入数值计算了不同弹射器数量对虚拟队列中舰载机的等待队长、系统等待耗时等关键指标的影响，使弹射器数量影响下的大型舰船舰载机出动能力得到了量化比较。计算结果表明，在给定条件下，甲板弹射器数量的增加能有效减少大型舰船舰载机出动时的排队等待现象，但在弹射器数量超过4部以后，这种良性影响将逐渐减弱。通过算例结论，验证了将排队论应用于大型舰船弹射器数量论证与设计的可行性。

弹射器数量；虚拟队列；排队论；出动能力

1 引言

对弹射起飞式甲板大型舰船，弹射器是决定其总体战斗力的基础装备，弹射器数量设计直接影响着舰载机的出动能力。

舰载机在大型舰船飞行甲板上弹射起飞前的等待问题可纳入运筹学的排队论范畴，甲板弹射器的数量直接决定着舰载机等待队列的各主要特征。如果弹射作业可以认为是舰载机接受弹射器服务的过程，那么每架待起飞的舰载机都相当于一位顾客，每部弹射器都相当于是一个服务台，其数量直接影响着舰载机获得弹射服务的效率。

本文应用排队论思想对舰载机的起飞等待过程进行了分析，从调运指挥官的角度提出了“虚拟队列”概念，建立了舰载机排队模型，在同等调运与弹射服务条件下，代入数值对数学模型进行计算，获得了不同弹射器数量条件下的舰载机排队系统各关键指标，进而明确了弹射器数量对大型舰船舰载机出动能力的影响。

2 舰载机等待过程的排队论描述

2.1 排队论应用于舰载机等待弹射问题的可行性

一个基本的排队系统主要由3部分组成，分别为输入过程、排队规则与服务［1－5］，对于舰载机等待接受弹射服务的过程，也可分为舰载机调运、舰载机列队等待与弹射起飞3个主要作业环节。机库内或甲板停机区的舰载机群相当于传统排队论中的顾客源，可独立工作的弹射器相当于传统排队论中的服务机构。根据以上分析，认为由于舰载机弹射作业与传统排队论中顾客接受服务的过程特征契合度较高，可以将排队论应用于舰载机等待过程的研究中。

2.2 舰载机“虚拟队列”与实际队列

当有舰载机接到任务需要弹射起飞时，可能暂时并没有弹射器可供使用，此时，舰载机处于等待状态。由于飞行甲板任务繁忙，空间有限［6］，舰载机不一定直接被调运至弹射器后排队，但却已经进入了起飞计划，对于调运指挥官来说，这些舰载机相当于已经被纳入了一支虚拟的起飞等待队列，可称之为“虚拟队列”。

而当舰载机真的需要调运至弹射器后方等待时，由于各部弹射器位置的不同或甲板空间有限等原因，机群不可能像虚拟队列一样排成一列，而是每部弹射器后方均有舰载机等待，如图1所示。

综上所述，研究弹射器数量与舰载机排队问题时，应对虚拟队列中的“单队列—多服务机构”形式排队系统与实际作业过程中的多个 “单队列—单服务机构”形式排队系统分别进行考察。

2.3 舰载机到达与弹射作业的时间分布

舰载机群到达等待队列的时间间隔分布与弹射作业过程的时间分布是舰载机排队问题中的重要参数。大型舰船携带有各种不同类型的舰载机，由于任务的突发性与多样性，各种飞机可能随时被要求起飞，通过对可靠资料的解读，认为舰载机被要求起飞执行任务的概率符合一定参数λ的负指数分布，根据排队论原理，负指数分布与Poisson 分布等价［7－10］，在计算中，可认为单位时间舰载机群按Poisson流到达等待队列。

从理论上讲，弹射器的工作流程固定，每次作业所耗费的时间也应该相同，但由于舰载机的型号不同、工作人员操作的熟练程度不同以及作业环境不同等原因，每架舰载机弹射作业过程的耗时可能会稍有不同，但经过大量统计，该作业耗时符合平均服务率为μ的负指数分布。

在大型舰船上的舰载机群排队系统中，由于一次飞行计划不可能包括舰上所有舰载机，所以，在建模过程中认为舰载机源为无限源。又因飞行甲板空间有限，在建模过程中，认为排队系统容量有限。

3 舰载机等待弹射的排队模型

3.1 虚拟队列的舰载机排队模型

根据上节所述，虚拟队列中的舰载机等待情况符合排队论中单队列、并列服务台、有限系统、无限源的负指数排队系统，弹射作业服从队列先后顺序，其基本排队模型可表达为M／M／C／N／∞模式（其中，前两个M分别表示舰载机加入队列的时间间隔与弹射器工作时间，均符合马尔可夫特性的负指数分布；C表示弹射器数量；N表示队列容量；∞表示舰载机来源无限），舰载机排队方式如图 2 所示［11］。

3.2 真实队列的舰载机排队模型

在飞行甲板上舰载机的真实弹射作业过程中，舰载机被分别调运至不同弹射器后的等待队列中，这样，便形成了多个并行服务的单队列、单服务台、有限系统、无限源的负指数排队系统，其基本排队模型可表达为M／M／1／N模式，舰载机群的排队方式如图4所示。

则稳态下整个系统中舰载机数量的数学期望为［8］LS＝ 0.5N。

由于甲板空间（系统容量）有限，当队列中舰载机的数量达到N时，剩余舰载机将暂时停止向等待队列的调运作业，则实际上舰载机的有效到达率为 λE＝λ（1－PN），那么，稳态下等待队列中舰载机数量的数学期望为LQ＝LS－λE／μ，平均每架舰载机在等待队列中的停留时间为WQ＝LS／λE－1／μ，在整个系统中，平均停留时间为 WS＝ LS／λE。

4 计算结果比较与分析

在实际作业过程中，由于甲板空间狭小且异常繁忙，舰载机通常很少真正地在弹射器后排队等待起飞，而是直接由指挥部门根据任务需求纳入起飞计划，即本文所述的“虚拟队列”，然后，在有空闲弹射器时将其调运至指定位置接受弹射，这样不仅可以节省甲板空间，而且相比于分配至每部弹射器后的真实等待队列，这种虚拟队列还可有效节省舰载机群的平均等待时间。

下面将应用算例，以舰载机虚拟队列为对象，通过对舰载机排队模型主要指标的比较来考察飞行甲板弹射器数量对舰载机出动回收能力的影响。

假设飞行甲板有C部弹射器，每部弹射器的工作均独立服从参数为μ＝0.6架／min的负指数分布，根据任务需要，某舰载机中队的机群以参数λ＝4架／min的Poisson流加入起飞计划，起飞波次容量为N＝24架。根据上节计算模型编制程序，可获得以上条件下当弹射器数量C分别为1、2、3、4、5、6时此排队系统的各关键指标，如表1所示。

表1 不同弹射器数量条件下虚拟排队系统的各关键指标Tab.1 Key targets of the dummy queue system under conditions of different quantity of catapults

由上表可见，随着飞行甲板弹射器数量C的增加，按本节所设定的条件，稳态下虚拟队列中舰载机数量的数学期望呈如图6所示的变化趋势。

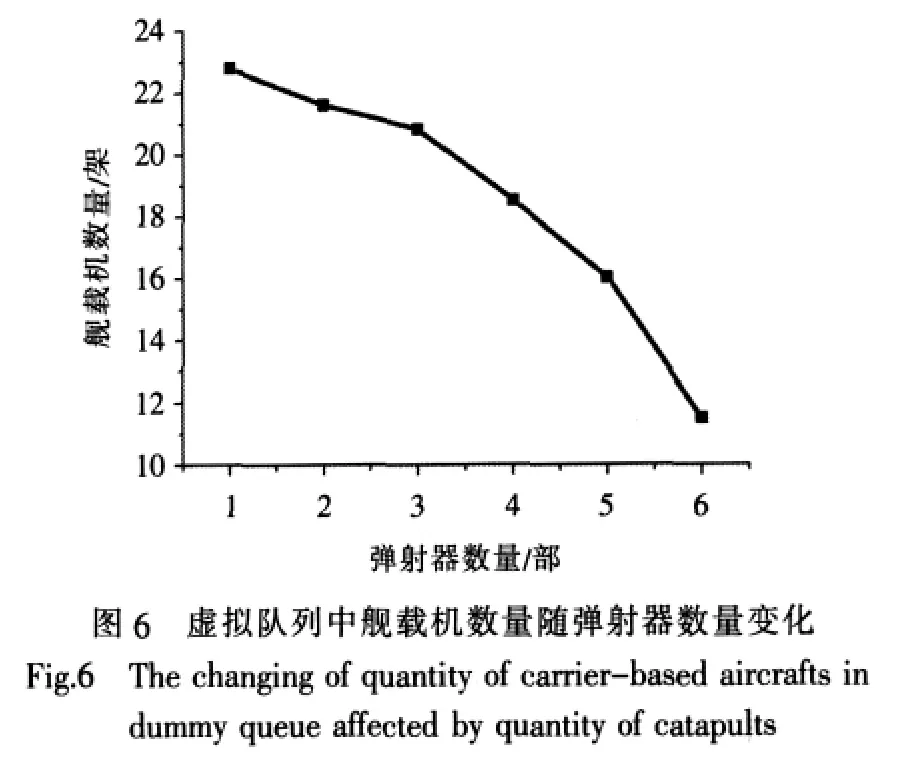
由以上变化趋势可见，随着飞行甲板弹射器数量的增加，起飞计划中舰载机虚拟队列的队长将明显变短，也就是说，飞行甲板弹射器数量的增加能明显减少大型舰船舰载机起飞的弹射等待现象，有效提高舰载机的出动能力。

舰载机群在整个等待系统中的平均耗时随弹射器数量的增加呈如图7所示的变化趋势。

由以上变化趋势可见，随着飞行甲板弹射器数量的增加，起飞计划中的舰载机群在虚拟队列系统中的等待耗时将明显变短，但是，当弹射器数量超过4部以后，弹射器数量的增加对此项指标的影响便开始减弱。

5 结束语

本文提出了舰载机“虚拟队列”的概念，并基于排队论思想对此问题进行了研究，通过相同的条件数值设定，求解了舰载机等待过程中虚拟队列工作模式下的各关键指标，对不同弹射器数量条件下舰载机出动前排队等待的主要指标进行了对比与分析，使舰载机排队等待过程中的各关键指标得到了量化。

根据计算结果与比较分析可知，在正常的甲板作业条件下，无论对于虚拟队列还是真实队列，弹射器数量的增加都将有效减少舰载机波次出动时的排队等待现象，有效提高大型舰船的舰载机出动能力，但当弹射器数量多于4部以后，弹射器数量的增加对舰载机出动能力的良性影响便开始逐渐减弱，这也充分说明了美国所有大型舰船为何在甲板面积充足的情况下只设置4部弹射器而没有使用更多的原因。

在下一步的研究中，应考虑计入大型舰船斜角甲板角度、各功能区域划分等因素对排队模型系统容量的影响，并综合考虑影响飞行甲板弹射器数量设置的其它因素，为我国此领域的相关研究建立更加可靠的理论依据。

［1］BORODIN A，KLEINBERG J，RAGHAVAN P，et al.Adversarial queuing theory［J］.Journal of the ACM，2001，48（1）： 13－38.

［2］ALMEIDA C F，SANT′ANNA J A，YAMASHITA Y，et al.Queuing theory models in urban passenger waterway transport terminals ［C］//Marine Technology V：Fifth International Conference on Marine Technology and Transportation.Poland，2003：225－234.

［3］ABDALLA A，BUCKLEY J J.Monte carlo methods in fuzzy queuing theory［J］.Journal Soft Computing－A Fusion of Foundations，Methodologies and Applications，2009，13（11）：1027－1033.

［4］RAMAN D，NAGALINGAM S V，GURD B W，et al.Quantity of material handling equipment－A queuing theory based approach［J］.Journal Robotics and Computer－Integrated Manufacturing，2009，25（2）： 348－357.

［5］YANG Gong －Ping，ZENG Guang－Zhou，LU Zhao －Xia.Study on the queuing mechanism of mobile agent system［J］.Chinese Journal of Computers.2005，28 （11）：1817－1822.

［6］黄胜，孟祥印，常欣.基于遗传算法的船体主甲板外展程度寻优［J］.海军工程大学学报，2009，21（4）：34－39.

［7］周智勇，陈峻，王炜.基于排队论的出行车辆停放接受条件［J］.东南大学学报（自然科学版），2006，36（4）：638－642.

［8］张宏斌.运筹学方法及其应用［M］.北京：清华大学出版社，2008.

［9］巴威，舒华，张芳凌，等.基于排队论的车辆装备维修力量需求预测研究 ［J］.军事交通学院学报，2009，11（6）：89－91.

［10］梁敬平，戎华，陈明荣.排队论在电子对抗侦察设备中的应用［J］.舰船电子对抗，2009，32（4）：92－95，112.

［11］刘敬贤，李昌伟，刘文.基于排队论的锚地规模论证分析［J］.船海工程，2009，38（4）：158－161.

［12］陈栋，邢昌凤.排队论方法在评估防空武器系统能力方面的应用 ［J］.海军工程大学学报，2003，15 （3）：110－114.

［13］张忠斌，王精业.基于排队论的装甲装备修理力量预测建模研究［J］.系统仿真学报，2006，18（增刊 2）：1017－1029，1023.

［14］宗群，魏利剑，程义菊，等.基于马尔可夫网络排队论的电梯交通建模及应用［J］.天津大学学报（自然科学与工程技术版），2005，38（1）：9－13.

Investigation into Deck Catapults Quantity of Large Ship by Using Queuing Theory

Zhou Xin-lei1 Meng Xiang－yin2Xie Xue－shen3 Hu Yu－long2 Hou Yuan－hang2
1 Department of Naval Equipment， Shenyang Division， Shenyang 110031， China
2 College of Shipbuilding Engineering，Harbin Engineering University， Harbin 150001，China
3 China Ship Development and Design Center， Wuhan 430064， China

The objective of this article is to establish a theoretical basis for determining the quantity of catapult on the flight deck of large ship.As for investigation， the approach of＂dummy queue （virtual queue）＂was presented from the view of aircraft handling officer， and the task flow model was set up and analysis was carried out by using the queuing theory.The realistic model of task flow of carrier－based aircraft in standby position for launch was also constructed.A multiple calculations were conducted for the key targets， ignoring all the other factors， with regard to the influence of different quantities of catapults on the virtual length of aircraft＇s waiting queue and time of the system standby based on the assumption of the queuing theory.The results enable to have a quantifying comparison of sortie generation capacities of carried－based aircraft on the flight deck.The calculations also showed that under a given set of conditions，increasing the quantity of the catapult can obviously minimize the queuing length of the birds waiting in a queue for launch on the flight deck， but， if the number of catapult was greater than four， this would be less effective.Through the calculating results， application of the queuing theory to the demonstration as well as quantity design of catapult on large ship is proved to be practicable.

catapult quantity； dummy queue； queuing theory； sortie generation

U664.4

A

1673－3185（2011）02－15－04

10.3969/j.issn.1673-3185.2011.02.003

2010-04-28

HZWQ 装备预先研究项目（10×××××01）

周鑫磊（1979－），男，工程师。研究方向：装备管理。E-mail：xiaoshitan＠sina.com