不同加载方式的斜齿轮接触分析

尹长城

（湖北汽车工业学院 汽车工程系，湖北 十堰 442002）

不同加载方式的斜齿轮接触分析

尹长城

（湖北汽车工业学院 汽车工程系，湖北 十堰 442002）

以一对相互啮合的渐开线斜齿轮为研究对象，通过APDL语言生成参数化几何模型，研究映射网格划分方式并建立了斜齿轮接触的有限元模型，基于非线性接触算法在不同加载方式下对齿轮啮合齿面的接触应力进行了分析，将仿真与赫兹计算结果进行了比较，讨论了不同加载方式对接触应力的影响。

有限元；斜齿轮；接触应力；不同加载方式

接触是在工程实际中经常遇到的课题。当2个固体的表面接触时区别为协调接触和非协调接触，当2个物体具有相似外形，相当接近的接触在一起，称这类接触是协调的，制动蹄及摩擦衬片与制动鼓的接触是协调接触［1］的例子。具有不相似外形的物体接触称为非协调的，例如齿轮接触。非协调接触通常接触面很小，也就是说，即使承受轻载作用，接触应力也很大，所以齿轮接触应力的分析计算受到国内外学者的广泛关注［2-5］。本文以一对相互啮合的斜齿轮为对象，利用有限元法计算齿轮齿面的接触应力，着重讨论不同加载方式的实现，最后将赫兹应力理论解与有限元数值解对比。

1 齿轮有限元网格模型的建立

表1 一对斜齿轮建模参数

在ANSYS中对斜齿轮副进行有限元接触分析，首先建立齿轮的有限元网格模型，根据表1所示斜齿轮啮合模型参数，利用APDL语言根据渐开线曲线方程和齿根过渡曲线方程以及啮合位置的旋转角度编制程序，绘制齿轮二维几何模型（图1）。

图1 二维齿轮的几何模型

大小齿轮的材料是40Cr，其弹性模量E为211GPa，泊松比μ为0.277。为得到合理的有限元模型，首先对二维齿轮进行映射网格划分，由于映射网格对模型要求比较苛刻，平面面积一般要求4条边，而二维齿轮模型的几何形状不符合映射网格划分的规则，需要把面分割成若干小的四边形，然后进行映射网格划分，部分轮齿面切割成简单的四边形如图2所示。在此基础上，将2维映射网格沿螺旋线拉伸成三维有限元网格模型，如图3～4所示。三维实体单元选择8节点6面体单元（SOLID185）。斜齿轮副有限元模型节点数103739，单元数85540。

图2 将齿轮面切割成四边形

图3 三维斜齿轮有限元网格模型

图4 部分齿映射网格

2 建立接触对

ANSYS程序支持面面接触单元，目标面一般是较刚表面，该表面在三维问题中用TARGE170单元来模拟，一般情况下，小齿轮比大齿轮更容易疲劳破坏，所以在制造过程中小齿轮表面刚度比大齿轮表面刚度大，所以此处的目标面为小齿轮齿面。接触面用CONTA174单元来模拟，接触面是大齿轮接触的齿面。本文共设置2个接触对，不同接触对应当通过不同的实常数设置来定义，但1个的接触对共享1个实常数。此处应该注意的是，齿轮接触为非协调接触，就是接触可能发生在模型变形过程中。一旦接触表面通过目标单元和接触单元被定义，它将跟踪变形的运动过程，一定要确保有接触存在的地方一定有节点存在。接触问题一般要求设置接触面的接触刚度，在网格满足精度的情况下，接触刚度越大，接触穿透就越小，精度就越高。但大的接触刚度值会造成收敛困难［6］，不但影响求解效率而且导致总体刚度矩阵变坏。ANSYS接触刚度系数一般在0.01～10内变化，为确定合适的接触刚度系数，应该从较低值开始，不断增大进行多次试算，直到接触应力变化较小为止。本文斜齿轮接触问题较为理想的接触刚度系数为3。

3 不同加载方式的接触应力结果

小齿轮在柱坐标下周向受到的驱动扭矩T为60 N·m，约束小齿轮内圈所有节点径向和轴向的自由度。此外对大齿轮内圈所有节点施加全约束。SOLID185单元只有3个方向平移自由度，并不具备转动自由度，所以不能在节点上施加扭矩，为了实现加载，本文采用3种不同的加载方式，并讨论各种方法的差异。

3.1 利用切向力施加扭矩

在节点上施加切向力是把小齿轮的驱动扭矩转化成沿其内径的切向力，切向力均匀分布在小齿轮内圈节点上，其值为驱动扭矩除以节点处的半径和节点数目，小齿轮内表面半径为22.7mm，内表面共2156个节点，故所施加切向力值为

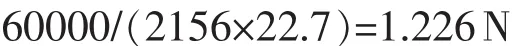
针对小齿轮在柱坐标的周向施加切向载荷，加载后模型如图5所示。计算后的接触应力图如图6所示，显示2个接触面的接触应力的结果。其中最大接触应力为378.1 MPa。

图5 切向力加载

图6 切向力加载方式接触应力图

3.2 利用表面效应单元施加扭矩

表面效应单元类似一层皮肤，覆盖在实体单元表面，主要功能是模拟表面层特性和施加各种表面载荷，表面效应单元是一种小刚度或无刚度效应的辅助单元，可以用来模拟结构覆盖层的许多特性。本文选择三维结构表面效应单元SURF154实现表面切向压力的施加。该单元具有3个平移自由度，只需要直接将小齿轮内表面的节点形成单元，并不增加模型的节点数，仅仅增加单元数目。利用单元的面号来控制不同的压力方向。压力载荷方向按照单元坐标系或局部坐标系施加在单元面上，若为小齿轮内表面施加切向压力，需建立局部柱坐标或将单元坐标系转换到柱坐标系下。所施加的切向压力值等于驱动扭矩除以小齿轮内表面面积和节点处的半径。即

利用表面效应单元加载后的模型，如图7所示，经计算，接触应力如图8所示。其中最大接触应力为384MPa。

图7 利用表面效应单元加载

图8 表面效应单元加载方式接触应力图

3.3 利用刚性区施加扭矩

刚性区是通过约束方程，将作用在主节点上的载荷自动传递到刚性区的其他从节点上。约束方程是描述多个不同的或相同的自由度之间的线性协调关系，可以连接不同类型单元之间的网格，连接具有不同自由度的单元。本文在小齿轮的几何中心点定义一个质量单元作为主节点，主节点上具有6个自由度，小齿轮内表面的节点是从节点，通过主节点与每个从节点之间建立UX、UY、UZ3个约束方程，建立刚性区。在主节点上施加MZ为60000 N·mm的扭矩，约束其它5个自由度，约束大齿轮内表面节点所有的平移自由度。刚性区施加扭矩示意图如图9所示，计算得到接触应力云图如图10所示，最大接触应力为371.2MPa。

4 斜齿轮接触理论赫兹应力计算

2个斜齿轮接触时，最初是在一条线上，在微小的载荷作用下，最初的接触线附近发生变形，致使它们在一个有限的区域上接触。这个区域比起两齿轮的尺寸来说是比较微小的。所以每个齿轮被看作是一个弹性半空间体，而且齿轮接触过程表面连续、小应变，当齿轮间的摩擦系数为零时，这些假设完全符合赫兹理论的假定［7］，故可用赫兹接触压力公式近似计算齿轮接触的接触应力［8］。

图9 利用刚性区加载示意图

图10 刚性区加载方式接触应力图

称为弹性影响系数，式中E1，E2，μ1，μ2分别为斜齿轮副的弹性模量和泊松比，代入材料参数计算得

所以端面重合度经计算得εα=1.515；式（1）中b为齿宽；T为小齿轮所受扭矩；d1为小齿轮分度圆直径；K为载荷系数，为使理论解与有限元解对比，而斜齿轮副模型属静力分析，故载荷系数取为1；u为大小齿轮齿数比，将本文各物理量数据代入式（1），计算得斜齿轮副的最大接触应力为

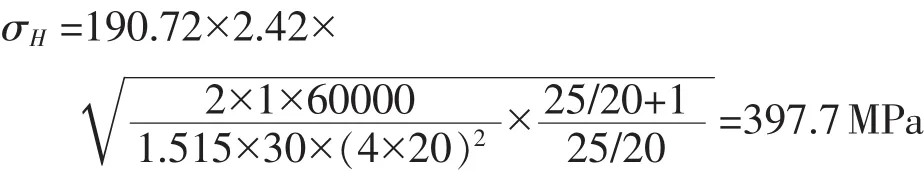
5 结果讨论

不同加载方式的最大接触应力值以及它们与理论解的比值如表2所示，理论解是利用赫兹理论将齿轮接触问题与2个圆柱体接触等效而推导出的公式，并且在公式中采用大量的修正系数，具有较大的误差，有限元的计算误差主要包括离散化误差和计算机的截断和舍入误差，如果能创建精细的有限元模型，网格密度和网格排列达到接触计算的要求，有限元解的精度将高于传统赫兹理论解。3种加载方式最大接触应力值都比理论解低，并且理论解没有考虑载荷系数（大于1）的影响。所以本文中理论校核是偏安全的。

表2 不同加载方式最大接触应力与理论解比较

切向力加载是将扭矩转化为切向力均匀的施加在节点上，并不需要载荷移置，有限元概念直观清楚。利用刚性区加载在有限元各种软件中最为常用，这种扇辐式刚性连接还有其他不同的应用，可在主节点上允许转动但限制平移，如果齿轮模型初始有间隙没有消除时，可在主节点施加一个小的转动作为第1个载荷步来消除刚体位移，接着使用一个空的载荷步把转角控制转为力矩控制，删除上步施加的转角后施加力矩进行求解，最后再施加用户需要的扭矩。刚性区方法使从节点的自由度从属主节点的自由度，这种方法通过约束方程使整个有限元模型的自由度降低。此外刚性区方法只适合小变

形，而且刚性区是虚构的，可能产生不可预料的反作用力和节点载荷，导致结果不准。表面效应单元加载是施加一个所使用单元不能接受的表面载荷，表面载荷一般是面力，施加在单元中需要节点移置，也就是说节点载荷是按照形函数原则将面力转化而来，不一定像切向力那样受力均匀。表面效应单元实现扭矩加载要求加载切向压力面是6面体单元，否则单元坐标系转换成柱坐标后，单元坐标系的周向并不沿表面的圆周方向。此外表面效应单元是支持大变形大应变的。

6 结论

本文实现了斜齿轮接触问题的3种加载方式，分别为切向力加载、表面效应单元加载、刚性区加载。其中切向力加载受力均匀，载荷加在节点处，最为直观，概念清楚。刚性区加载应用广泛，应用刚性区处要求必须是小变形，该法建立的约束方程使整体自由度降低，表面效应单元支持大变形大应变，但一般对网格有严格要求。

利用有限元法能有效的计算齿轮接触问题，求解方法和加载方式多样化，比传统赫兹理论计算更真实、更精确。

［1］马迅，尹长城，陈艳红.基于ANSYS Workbench的鼓式制动器的接触分析 ［J］.湖北汽车工业学院学报，2010，24（3）：1-3.

［2］凡增辉，赵熙雍，晏红文.基于ANSYS的斜齿轮接触有限元分析［J］.机械传动，2010（4）：68-70.

［3］杨生华.齿轮接触有限元分析［J］.计算力学学报，2003（2）：189-194.

［4］吴胜军.渐开线直齿轮动态接触仿真分析［J］.湖北汽车工业学院学报，2010，24（1）:31-34.

［5］Barlam D,Zahavi E.The reliability of solutions in contact problem s ［J］.Comp&Struct,1999,70:35-45.

［6］Guan Dihua and Jiang Dongying.A Study on Disc Brake Squeal using Finite Element Methods ［J］.SAE No.980597,1998.

［7］Johnson K L.接触力学［M］.徐秉业，译.北京：高等教育出版社，1992.

［8］濮良贵，纪名刚.机械设计［M］.北京：高等教育出版社，2001.

Contact Analysis of Helical Gears Based on Different Loading Ways

Yin Changcheng
（Dept.of Automotive Engineering,Hubei Automotive Industries Institute,Shiyan 442002,China）

Taking a pair of meshing involute helical gears as the research object，the parameter geometrical model was generated by APDL.According to the mapping mesh algorithm,the finite element model was established for the helical gear contact.The simulation analysis of contact stress on engagement surface was carried out based on the nonlinear contact algorithm and different loading ways.The new method was compared with the traditional Hertz theory.The influence of the different loading ways on contact stress was discussed.

finite element;helical gear;contact stress;different loading ways

TP39

A

1008-5483（2011）02-0028-04

2011-05-23

湖北省教育厅优秀中青年课题（Q20082301）

尹长城（1976-），男，吉林大安人，硕士，从事汽车结构有限元分析研究。