库水位骤降时坝坡稳定性分析研究
刘英泉,王成言
(中水北方勘测设计研究有限责任公司,天津300222)
土石坝坝坡稳定性决定于它的几何形状、土体材料属性及其内外部受力情况。在目前的研究中,认为孔隙水压力和库水压力是影响坝坡稳定性的主要荷载[1-2]。库水位的变化会引起土体中孔隙水压力的瞬态变化,同时库水压力的变化也会产生坝坡内部超孔隙水压力的发展[3-4]。当库水位下降过快,没有给排水提供足够的时间,对于渗透系数较小的土体,其孔隙水压力不会在水位骤降期以同样的速率伴随着水位的下降而消散。因此,研究低渗流土体在库水位骤降期的特性是很有必要的[5-7]。
本文研究库水位骤降时,坝坡渗流场及稳定性的变化情况,并用有限元法研究不同工况下孔隙水压力随水位骤降的变化;将计算得出的不同时刻孔隙水压力值应用于采用极限平衡法,分析边坡稳定性。在理论研究的基础上,结合某均质土石坝具体情况对其渗流场变化条件下的坝坡稳定性进行分析,总结了坝坡稳定性对库水位变化的响应情况。
1 基本理论
在实际工程中,降雨入渗和库水位变化中的土坝渗流都应该考虑非饱和区的作用。考虑非饱和渗流的边坡稳定分析问题以及求解比较复杂,包含了岩土体、水、空气以及收缩膜四相的互相耦合问题。本文分析库水位骤降时坝体的浸润线变化和孔隙水压力的变化。
根据达西定律,多孔饱和不可压缩连续介质渗流可表示为:

式中:φ为总流体势或总水头;k(p)为介质的渗透系数;Q为源、汇项;S为储水系数。
其中

式中:ks是饱和渗透系数,为常数;f(p)为关于压力水头p的光滑连续函数[1]。
结合有限元理论,由式(1)可得:

式中:[ks]为饱和单元渗透系数矩阵;[kus]为非饱和单元渗透系数矩阵;[ps]为饱和单元孔隙率矩阵;[pus]为非饱和单元空隙率矩阵;{q}为节点水头向量;{Q}为临界节点流向量。
微分方程(3)整合了时间域,结合平衡方程和连续方程,可以通过迭代计算出自由面及渗流场分布。
通过有限元瞬态渗流分析得出水位骤降后某一时刻自由面,对于滑动面在浸润面以下的情况,可采用考虑孔隙水压力影响的有效应力方法来计算土坡的安全系数,再结合Morgenstern-Price提出的非饱和土体的强度理论,土质边坡的安全系数公式可写为:

式中:Fs为边坡稳定系数;c′i,φ′i为土体的有效应力抗剪强度指标;φbi表示由于基质吸力增加引起抗剪强度增加的吸力摩擦角;γ为土的天然容重;θi为条块底面中点的切线与水平面的夹角;bi为土条宽度;pwi为孔隙水压力;hi为土条高度;li为土条滑动面最大弦长。
根据式(4)结合有限元渗流分析得出的孔隙水压力等结果,定义材料参数后可搜索出临界滑移面,计算出坝坡安全系数。
2 实例分析
2.1 非稳定渗流场分析
2.1.1 计算模型
某水利枢纽工程位于陕北黄土高塬南部的黄土梁峁区,拦河坝为均质土坝,大坝坝顶高程852.0 m,坝顶宽度10 m,最大坝高66.0 m,坝顶总长度为502.0 m;上游坝坡坡比为1∶2.75和1∶3,在830 m高程处设置3 m宽的马道;下游坝坡坡比均为1∶2.75,在836 m高程和816 m高程处设置2 m宽的马道。上游坝坡采用0.4 m厚的干砌石护坡,下游坝坡采用浆砌石网格内植草护坡,并在坝体内设置水平褥垫排水,排水褥垫深入坝体内140 m,布置形式见图1。
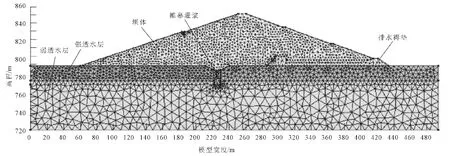
图1 计算模型网格剖分图
根据项目具体情况取河床坝段最大坝高处建立如图1所示有限元模型。边界条件为:上游边界条件随时间变化,即从高程848 m到高程800 m进行瞬态分析。坝基的上游侧面、下游侧面以及底面为零流量边界;强透水层上游顶面及下游顶面、上游库水位以下的坝坡表面及下游尾水位以下的下游坝坡表面为定水头边界。
运用Geo-Studio建立起二维有限元模型,包括坝体、防渗帷幕、排水褥垫、强透水层、弱透水层五个区。该有限元计算模型共剖分了 2 582个节点,4 536个单元。模型渗流、稳定计算参数和计算工况分别如表1、表2所示。

表1 渗流、稳定计算所需参数表

表2 计算工况
2.1.2 计算结果分析
图2~图5为库水位以不同速度下降时坝体浸润线位置的变化图。图中的数字是浸润线位置的时刻(单位:d)。

图2 工况1时浸润线位置变化图

图3 工况2时浸润线位置变化图

图4 工况3时浸润线位置变化图
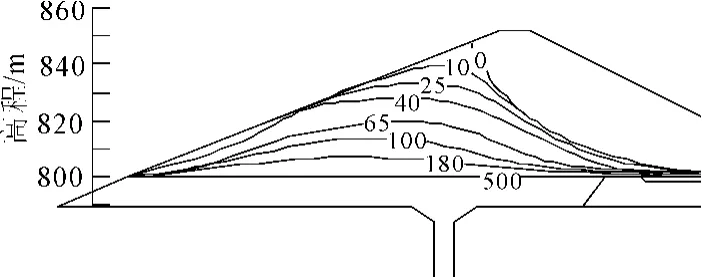
图5 工况4时浸润线位置变化图
库水位下降速度为0.5m/d时(如图2),浸润线在35 d后才出现上凸形状,且不是特别严重;当库水位降至800 m时,浸润线最高点高程为808 m。在库水位下降速度为1 m/d时(如图3),浸润线变化滞后于坝前水位变化而出现向上游坝坡渗流的现象仍较明显,浸润线形状上凸;当库水位降至800 m时,浸润线最高点高程为818 m。
当库水位下降速度为1.5m/d时(如图4),浸润线滞后现象更为明显。库水位下降速度为2 m/d时(如图5),“逆流”现象最严重,在10 d时,坝前水位已经降到828 m,而浸润线最高点高程为843 m,且出现在上游坝面。靠近上游坝面的坝体大多还是饱和的,坝体内浸润线回落严重滞后于库水位下降的速度。
由图2~图5可以看出,随着库水位下降,坝体内的浸润线也随之下降,坝体内浸润线下降有明显的滞后现象。部分水由于孔隙水压力来不及消散而滞留在坝体内,使得浸润线呈现“上凸”的曲线形状。坝体内自由水面高于上游库水位,形成“逆流”现象。水位下降速度越快,“逆流”现象越明显。不同水位下降速度下,浸润线在经过450 d后都基本上趋于稳定。
2.2 上游坝坡稳定性分析
库水位骤降情况下坝体内孔隙水压力消散滞后及上游坝坡的“逆流”现象定会对上游坝坡稳定性造成不利影响。图6为不同工况下上游坝坡安全系数随水位下降时间变化情况图。

图6 库水位下降时上游坝坡的安全系数变化曲线图
上游坝坡的安全系数随库水位变化,原因如下:第一,坝前水体对坝体的静水压力有利于上游坝坡稳定,上游水位下降自然导致上游坝坡稳定安全系数降低;第二,库水位下降过快,坝体内孔隙水压力来不及消散而形成向上游坝坡的反向渗流所致。渗透力在库水位下降过程中是变化的,渗透力达到最大值的时候坝坡安全系数将达到最小值。
由图6可看出,工况4为水位下降速度最快的工况,其上游坝坡安全系数谷值最小且达到谷值所需时间最短。结合工况4~工况1,水位下降速度越慢,上游坝坡安全系数所达到的低谷值越小,达到低谷值的时间也越长。水位下降速度越快渗透力越容易达到最大值,随着水位骤降速度的减慢,坝坡稳定系数的最小值逐渐变大,发生的时间也越晚。因此,水位骤降速度是影响上游坝坡稳定性的重要因素,水位骤降速度越大对上游坝坡稳定性不利。
3 结 论
本文考虑非饱和条件下某工程非稳定渗流,将渗流场模拟得出的孔隙水压力等结果应用于上游坝坡的稳定性分析中,得出以下结论:
(1)在库水位骤降情况下,坝体内的浸润线随之下降,但有明显的滞后现象。部分水由于孔隙水压力来不及消散而滞留在坝体内,坝体内浸润线高于上游库水位,形成向上游坝坡的“逆流”。“逆流”现象产生的渗透压力对上游坝坡稳定性产生不利影响。
(2)库水下降速度不同时,开始出现“逆流”现象以及形成稳定渗流场的时间是不一样的。库水位下降速度越快,上游坝坡稳定性降低速度及幅度越大。
[1] 沈珠江.广义吸力和非饱和土的统一变形理论[J].岩土工程学报,1996,18(2):1-9.
[2] 刘新喜,夏元友,张显书,等.库水位下降对滑坡稳定性的影响[J].岩石力学与工程学报,2005,24(8):1439-1444.
[3] 邓祥辉.等效连续岩体的渗流应力耦合模型研究及应用[J].西安工业大学学报,2009,29(6):585-588.
[4] 刘新喜,夏元友,练操,等.库水位骤降时的滑坡稳定性评价方法研究[J].岩土力学,2005,26(9):1427-1431.
[5] 王学武,许尚杰,党发宁,等.水位骤降时的非饱和坝坡稳定分析[J].岩土力学,2010,31(9):2760-2764.
[6] 贾苍琴,黄茂松,王贵和,等.水位骤降对土坡稳定性的影响分析[J].同济大学学报(自然科学版),2008,36(3):304-309.
[7] Lane P A,Griffiths D V.Assessment of stability of slopes under drawdown conditions[J].Journal of Geotechnique Geoenvironment Engineering,2000,126(5):443-450.
- 水利与建筑工程学报的其它文章
- 江口水电站椭圆型双曲拱坝设计特点
- 真空预压地基处理的加固深度研究

