基于图像片的模糊C均值聚类图像分割

顾建伟

(南通大学现代教育技术中心，江苏 南通 226000)

1.引言

图像分割是指把图像分成具有不同特性的区域并提出感兴趣的目标，它是图像处理到图像分析的关键步骤。近年来，模糊C均值(FCM)算法[1，2]作为一种无监督聚类算法已成功应用在医疗诊断、目标识别和图像分割等领域，其主要目的在于将向量空间的样本点按照某种距离度量划分成一定数量的子空间。

基于图像片的图像处理思想[3-4]是近年来刚刚兴起的用于去除图像噪声的一种方法，其基本原理是将原先图像处理中的点用局部图像片来替代，增加了单个像素点的计算信息，在图像去噪领域得到了很好的应用。本文将这种以片代点的思想应用于基于模糊聚类方法的图像分割，通过实验证明本文的方法很好地克服了基于FCM图像分割所存在的问题，同时该方法也为聚类分割提供了一种全新的思路。

2.模糊C均值聚类

2.1 传统模糊C均值算法(FCM)

模糊聚类由Dunn[1]首先提出，并由Bezdek[2]推广为一般的模糊C均值聚类算法。该算法通过最小化一个二次目标函数，将数据集(图像)划分为若干类。

FCM算法中目标函数定义如下：

其中，U={uik}∈Rn×c为隶属度矩阵，V={v1，v2，…，vc}∈Rc×p为c个聚类中心的集合，m∈[1，∞]为加权指数，通过大量研究表明，m的最佳选择范围为[1.5，2.5]，通常取m=2较为理想。dik=||xk-vi||A表示第k个样本到第i类中心vi的距离，||·||A表示A范数，一般定义为欧氏距离。

FCM的目标函数可以通过迭代更新隶属度矩阵U和聚类中心集合V达到最优解：

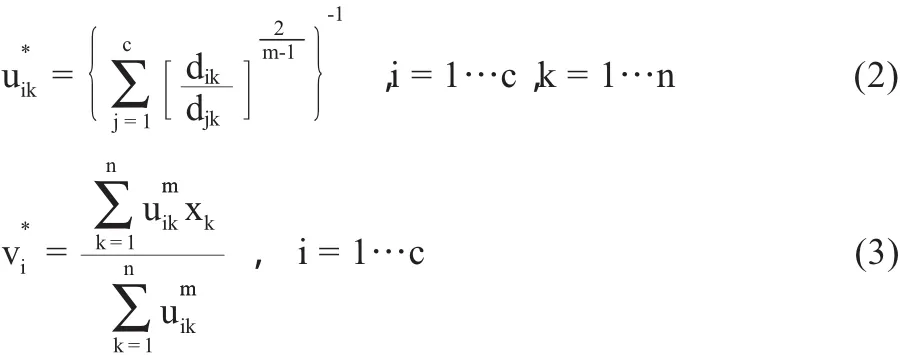
不断更新上述两式直到聚类中心集合V的变化值小于设定值ε(ε>0)。

传统的FCM算法在图像处理过程中主要存在两方面的缺陷：一是对于图像噪声的敏感，这主要是因为传统的FCM算法仅仅考虑了图像各个像素点灰度值之间的差别而没有将图像的其它信息考虑进去，例如空间信息等；另一个就是隶属度函数非单峰值的现象[4]。一般认为，当某一点属于某一类时，该点所对应隶属度的值应该趋向于1，该点其它类对应隶属度的值趋向于0，这就是本文所说的单峰值，如图1(a)所示。但是通过(2)式计算所得的FCM隶属度uik并无法满足单峰值特性。图1(b)中，u1(x)，u2(x)，u3(x)是FCM的隶属度分布情况，聚类中心为v1=1，v2=3，v3=8。u1(x)在5附近达到局部最大值，因此u1(x)并非单峰值。这种非单峰值的现象在一定程度会影响分类结果。图1(c)为本文方法的隶属度分布。

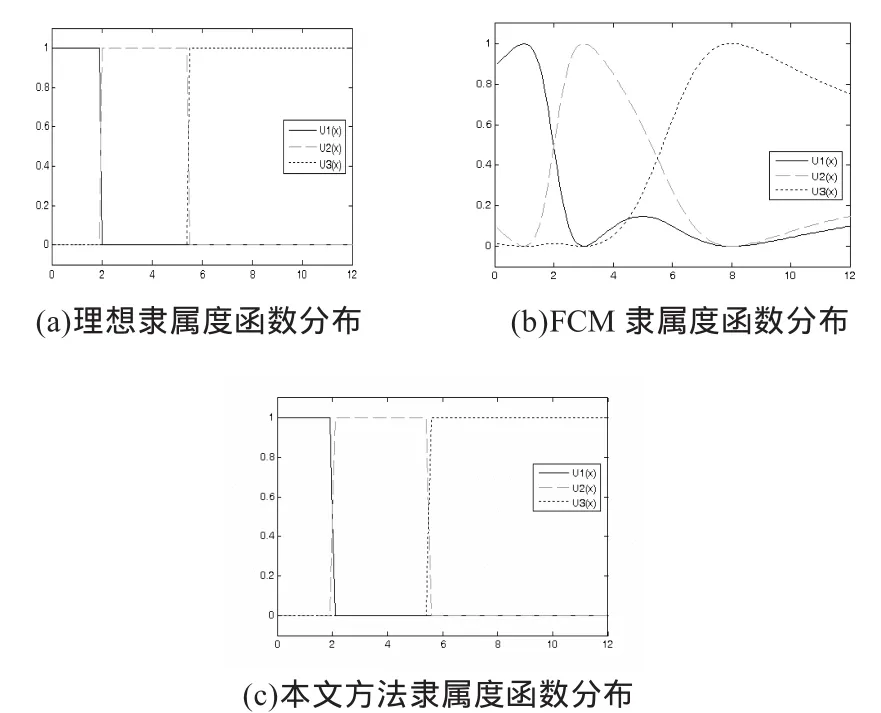
图1 一维信号的隶属度分布

2.2 FCM的改进算法

为了克服FCM对于图像噪声的敏感性，自FCM被提出之后，人们对其抗噪性进行了大量的研究。因此在传统FCM算法中加入空间约束成为研究的热点。

Ahmed等人[5]于2002年提出了BCFCM，将像素点的局部区域均值引入到传统的FCM目标函数中，以达到抗噪效果，其目标函数如下：

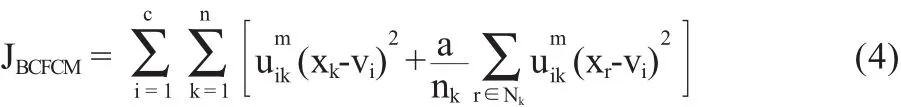
其中xr表示以k点为中心的邻域Nk中像素点的灰度值，nk为集合Nk的势，即Nk中的像素个数。参数用来控制该局部项对于全局的影响。在此基础上，Chen等人[6]提出了BCFCM的快速算法，FCM_S1和FCM_S2，通过提前计算出各个像素点的局部均值来提高算法速度。

随后，Szilágyi等人[7]将BCFCM算法流程重组，提出了EnFCM。他们首先对图像进行均值滤波，如下：

其中，ζk表示各个像素点滤波后的灰度值。其目标函数为：

式中，hl表示图像中灰度级为l，l∈{1，2，…L}总像素点个数，L为图像的灰度级个数，对于一般的灰度图像而言，L=256。相应的更新函数为：

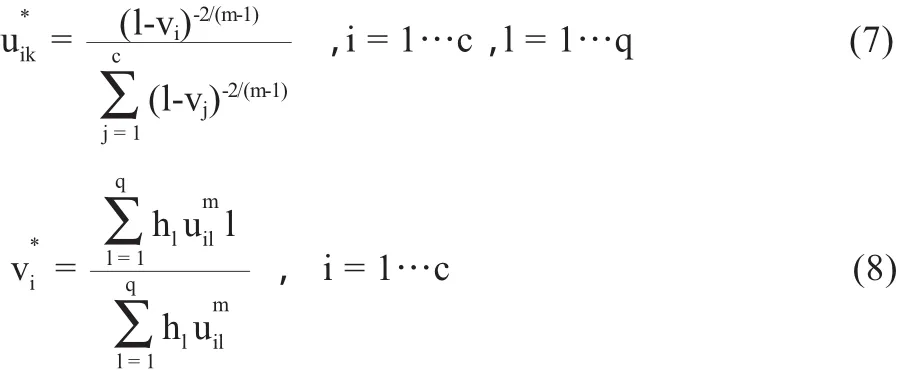
无论是经典的BCFCM还是改进的MFGFCM都不可避免地需要通过一些控制参数来控制局部区域约束项，而这些参数的设定往往都要根据具体实验而定，无法提出一个统一的标准方法，在实现及使用过程中，参数的设定较为繁琐。针对此问题，本文提出了一种全新的聚类方法。使用图像片来代替单个像素点的计算，不仅拉大了像素点与聚类中心之间的距离，使得聚类精度更高，同时消除了目标函数中的局部区域控制项，与传统FCM相比，在参数设置方面仅仅增加了一个片窗口大小的设置，就能够达到更好的抗噪性能。另一方面，本文还有效地消除了由于FCM所导致的隶属度函数的非单峰值现象，与理想的隶属度函数分布十分相近，以达到提高分割精度的目的。

3.基于图像片的模糊C均值聚类的图像分割方法

3.1 图像片的思想

图像片的思想来源于图像去噪领域中的一种非局部平均的图像去噪方法[3-4]，其基本思想是利用图像的局部相似信息来代替单个像素点的相似信息。这里所谓的局部相似信息即图像片。图像片包含更多的图像信息，能够比单个像素点更好描述图像的特征，因此基于图像片的图像去噪方法能够更好地保持纹理等具有重复结构的特征。本文正是在借鉴这种方法的基础上，将图像片的思想用于聚类分割算法中，以图像片代替单个像素点，通过计算图像片与聚类中心的相似性，增加像素点与聚类中心的距离，虽然在一定程度上拉大了像素点与其所对应聚类中心的距离，但同时也大大增加了该点与其它聚类中心的距离，这样从整体看来，该方法可以使分类更加精确。另一方面，以片代点的思想，可以很好地克服单个像素点灰度值对于分类的绝对影响，即克服噪声的影响，从而达到抗噪目的。本文正是使用图像片来代替单个像素点，通过计算图像片与聚类中心之间的欧氏距离，来计算该片中心点的隶属度，达到对该点进行分类的目的。

3.2 本文算法

本文将图像片代替像素点的思想用于聚类分割，提出了基于图像片的模糊C均值聚类(IPFCM)方法。

令I：Ω→Rn为定义在连续域Ω⊂R2上的二维图像，当n=1时，表示灰度图像；当n=3时，表示彩色图像。本文以灰度图像为例进行介绍。

即图像中的每一个像素点都对应一个q2维的向量。这对应的目标函数为：

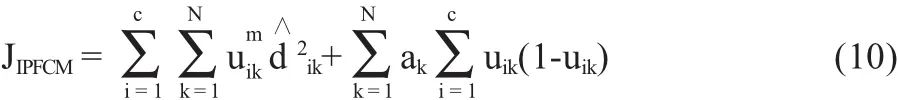
其中，U={uik}∈RN×c为隶属度矩阵，V=(v1，v2，…，vc)为c个聚类中心的集合，N为图像中总像素数，m∈[1，∞]为加权指数，取值与FCM相同。=||||A表示第k个图像片到第i类中心vi的距离，由于片PIk为一个向量，可以采用两种方式来计算该距离，一是用向量均值，二是用向量总和，为了提高计算速度，本文采用向量均值来计算该距离：

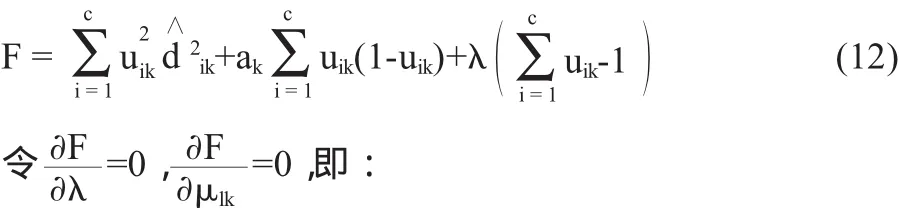
通过式(16)可以看出，本文方法可以很好的控制隶属度函数的单峰值性，如图1(c)所示，从中发现本文的隶属度函数分布与理想分布十分接近，这就很好的克服了FCM方法中非单峰值的特点，进而保证了聚类的精确性。聚类中心集合V的更新如下：

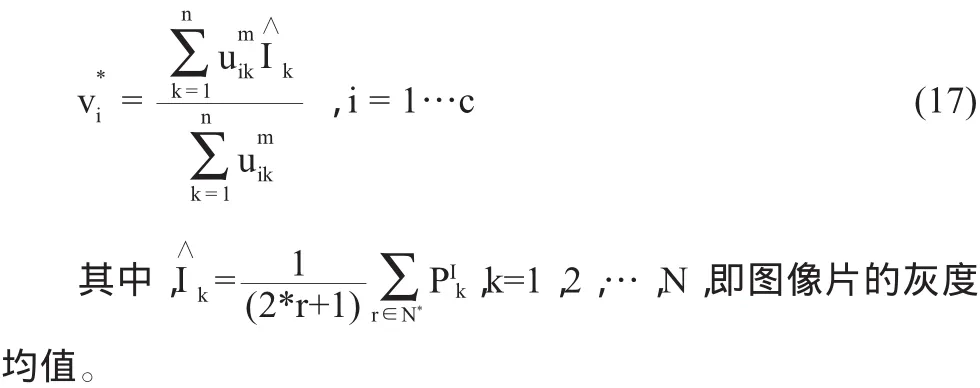
3.3 算法流程

本文算法具体流程如下：

步骤一：初始化参数，设置m=2，ε=0.01，c初始化聚类中心集合V。一般而言，对于灰度图像，在0到255的范围内随机生成c个整数，作为V的初始值，并通过更新达到最佳聚类中心值；

步骤二：设置图像片邻域窗口半径r，并根据公式(9)将图像中每一个像素点扩展为q2维的向量，其中q=2r+1；

步骤三：根据公式(16)更新隶属度矩阵U；

步骤四：根据公式(17)更新聚类中心V；

步骤五：比较更新前后的聚类中心，如果||Vnew-Vold||＜ε，则停止迭代输出结果图像；否则回到步骤三继续更新迭代。

4.实验结果

首先讨论图像片半径的选取，再对人工合成灰度图像不同方法的实验结果进行定量比较；最后对医学图像进行实验。

4.1 图像片大小的选择

与FCM相比，本文唯一的额外参数为图像片半径r的设置。r越大，聚类分割的抗噪性越强，但在增加算法时间复杂度的同时容易造成图像边缘点的误分类；r越小，虽然提高了图像的分割精度，减小了算法的时间复杂度，却是以牺牲抗噪性为代价的。如图2所示，第一行为噪声较小的不同图像片半径的分割结果；第二行为噪声较大的不同图像片半径的分割结果。图2中，对于噪声较小的图像而言，r=1的图像片克服图像中噪声影响的同时，很好的保持了图像边缘，在区域的交界处误分类点数很少，随着的增大，区域交界处愈加的不平滑，r=3时图像区域交界处甚至出现了“过渡区域”。当图像噪声较大时，r=1的图像片的抗噪效果明显不如r=3的图像片，但是r=3时图像区域交界处出现“过渡区域”，这将导致分割精度的大幅度降低。对于实际图像而言，虽然噪声是不可避免的，但其强度相对较低，同时结构比较复杂，图像各个区域交界处较多，因此一般采用r=1的图像片来进行处理。

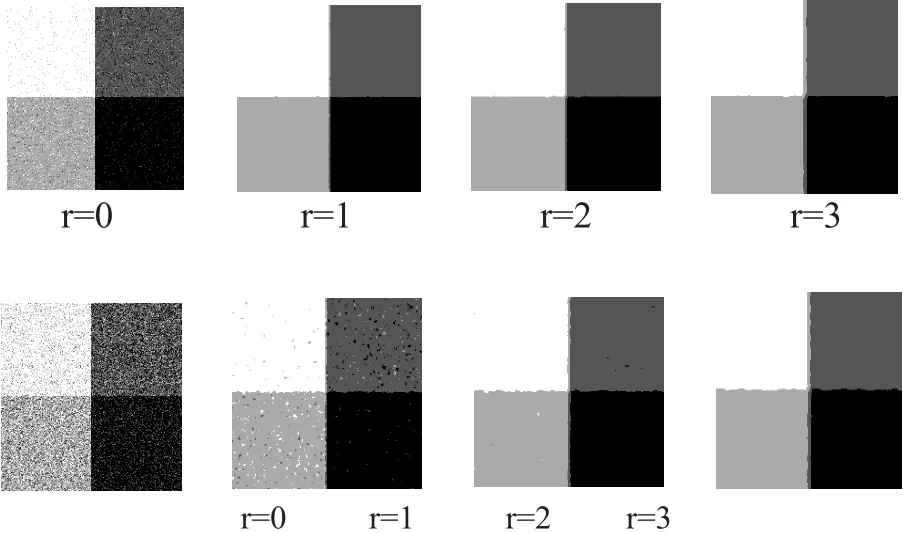
图2 不同噪声不同图像片大小的分割结果

图3显示了本文方法不同图像片大小的图像分割结果。图像来源于BrainWeb1，原图为加噪9%的MR脑图像。对比实验显示出，随着图像片半径的增大，分割结果变得更为平滑，灰质与白质的边缘部分细节丢失更为严重。

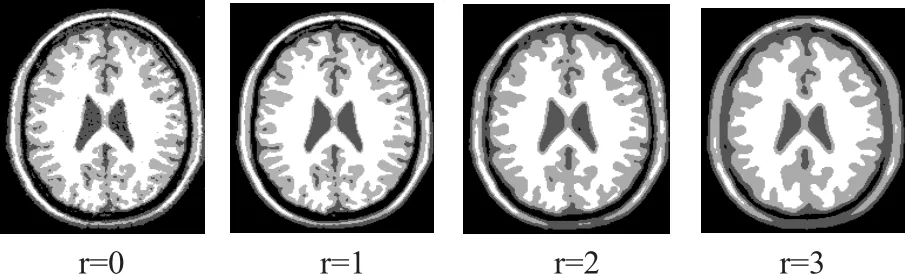
图3 不同图像片对加噪9%图像的分割结果

本文对MR图像的分割精度进行了定量分析。目前，已有很多种图像分割精度的评判标准，本文采用较常用的两种方法：JS(Jaccard similarity)方法[8]和DC(Dice coefficient)方法[8]，其度量公式依次为：

(18)、(19)式中，S1，S2表示需要比较的两幅分割结果，这里使用分类分割后的结果与BrainWeb中的人工分割结果进行比较。|·|表示相应区域中的像素点个数。这里采用公式(18)对图3的分割结果进行精度计算，如表1所示。通过表1的定量分析证明了上述现象。尽管很好的克服了噪声的影响，但是图像分割精度过差，r越大分割精度也就越低，无法满足实际需要。当r=0时，此时的IPFCM方法退化为FCM方法，分割图像的细节能够得到较好的保持，但对于噪声的敏感性是无法避免的，这也是FCM本身无法克服的缺陷。从实验结果可以看出，r=1的图像片处理结果无论在分割精度、细节保持还是克服噪声方面，都具有很好的效果。

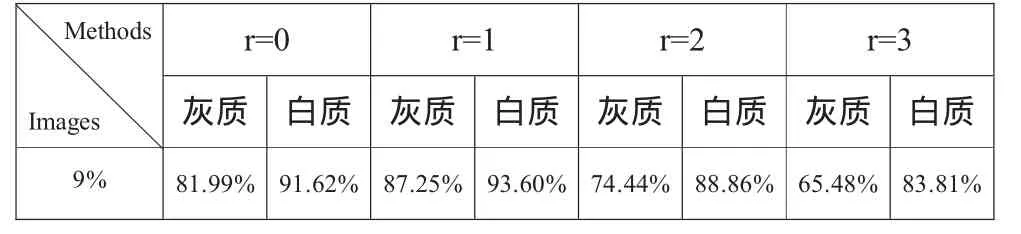
表1 不同图像片对加噪9%图像的分割结果精度计算(JS)

实验过程中，基本参数设定为：m=2，ε=0.01，所有聚类方法均使用半径r=1的窗口，人工合成图像中c=3，医学图像中c=4，聚类中心则根据c的大小随机生成相应的聚类中心集。

4.2 合成图像

图4为各个聚类方法的分割结果比较。该图像来自IBSR，选用256*256大小的带噪图像对FCM、BCFCM、En-FCM、FGFCM、MFGFCM、IPFCM这六种方法进行方法比较。其中，只有FCM与IPFCM不需要额外的参数设定，BCFCM、EnFCM、FGFCM、MFGFCM均需要一个或几个控制参数，这些参数的设定并非本文重点，这里不一一列举。图4中，FCM方法对于噪声的敏感显而易见，BCFCM不仅无法达到满意的抗噪结果，其效率也十分低下，运行开销较大；EnFCM与FGFCM方法虽然比较地好提高了运行速度，但是分割结果还是可以看到该方法无法消除的部分噪声；从结果来看，MFGFCM与IPFCM的抗噪性最好，细节上本文方法要优于MFGFCM。

图4 各种聚类分割方法比较

对于合成图像的分割精度计算，采用如下公式：

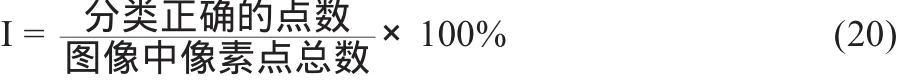
计算结果如表2所示。通过表2的对比，在相同噪声的情况下，IPFCM的分割精度最高。这些噪声图像都是在图4 (a)的原图基础上增加不同的噪声，其中，Gaussian1、Gaussian2、Gaussian3都是均值为0，方差依次为0.01、0.03、0.05的高斯白噪声；Impluse为椒盐噪声；M ixed1、M ixed2分别为方差为0.04、0.08的混合噪声。

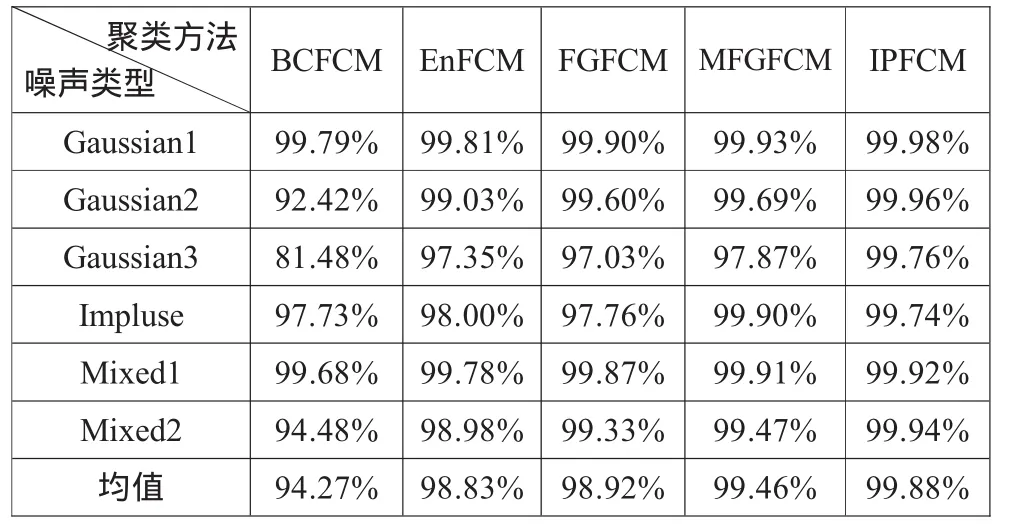
表2 不同噪声水平下各方法分割精度的定量分析

由于噪声强度问题，以上分析只能体现出MFGFCM与IPFCM拥有较好的抗噪性，但两者之间的比较不够突出，图5使用了另外一幅合成图像，从中明显可以看出IPFCM的抗噪性明显优于MFGFCM。

图5 MFGFCM与IPFCM方法比较

4.3 MR脑图像

本文对核磁共振(MR)图像使用EnFCM、MFGFCM、IPFCM三种方法在不同噪声水平下的分割结果进行比较。由于本文是针对聚类方法提出的新思想，而不是针对脑图像应用，没有加入MR脑图像去偏移场的计算，因此本文选用T1模态1mm切片厚度无偏移场的不同噪声水平下的脑图片，图6第一列的三幅图像分别为加噪0%、3%、9%的第96针脑图像，其分割结果如图6第二至第四列图像所示。

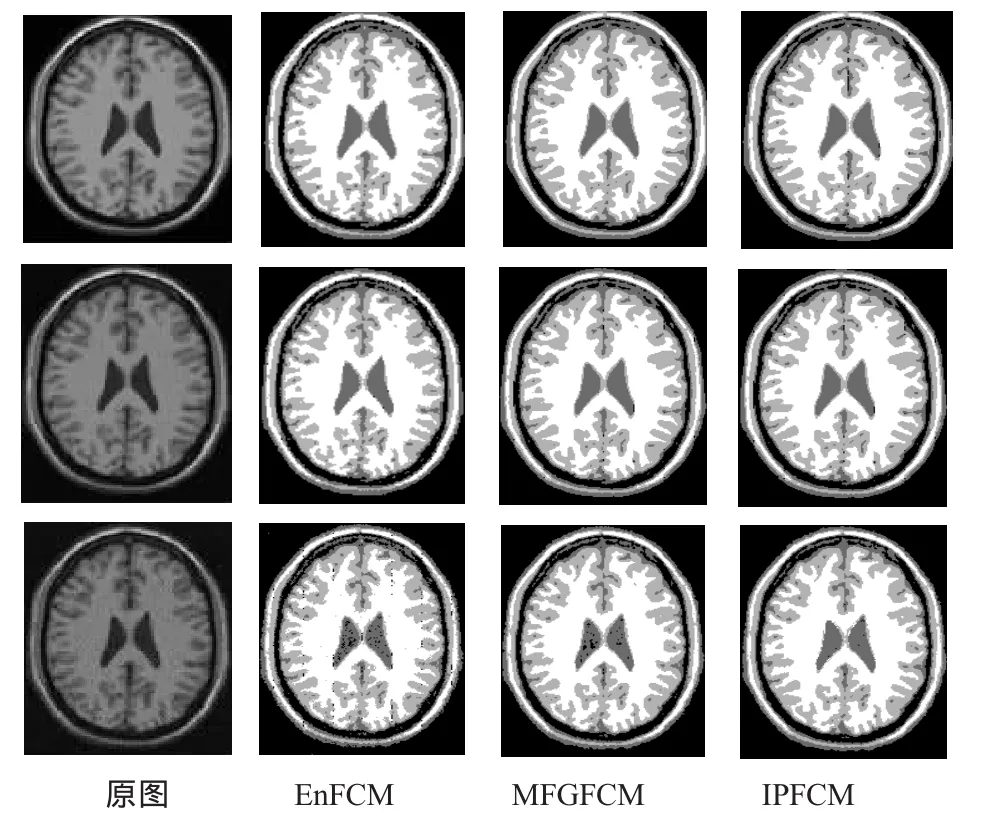
图6 EnFCM、MFGFCM、IPFCM方法MR脑图像分割结果

通过EnFCM、MFGFCM、IPFCM三种方法的比较，还是可以看出IPFCM在抗噪方面是最好的。

表3列出了图6中各种方法分割后灰质、白质的分割精度。通过定量分析得出在克服噪声影响的同时IPFCM在同类方法中的分割精度较高，且无需过多参数设定，具有较强的可靠性。

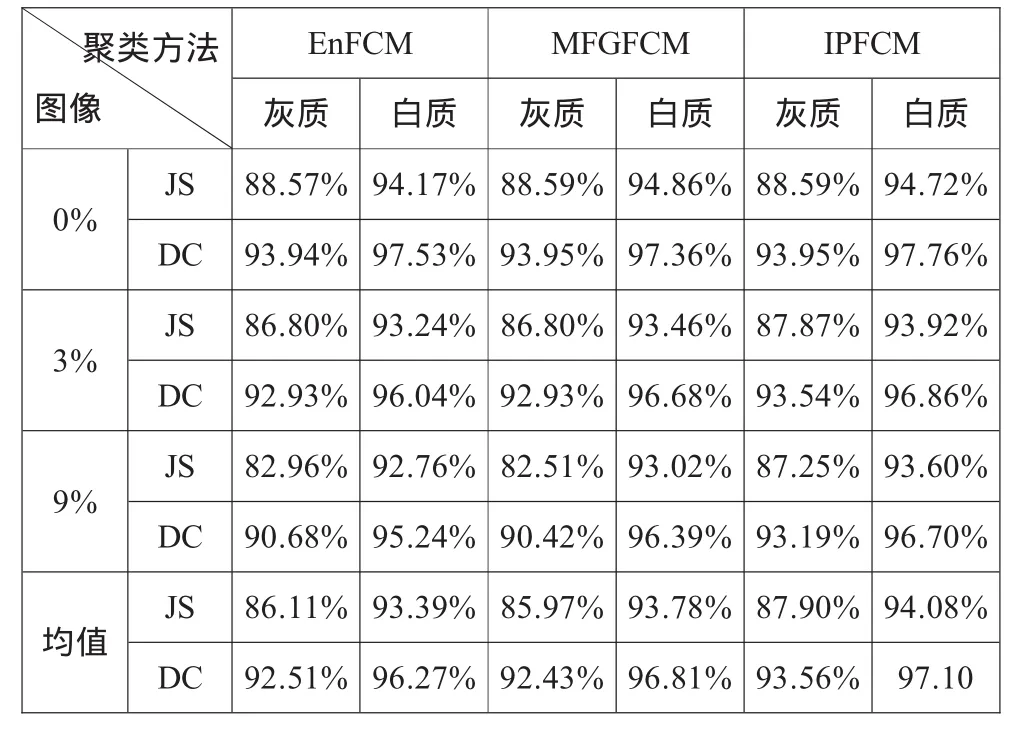
表3 EnFCM、MGFCM、IPFCM方法分割结果精度计算(JS、DC)

以上多组不同类型的实验，对IPFCM进行了全面的分析，不仅表明了IPFCM的有效性和精确性，同时还对图像片半径的选择进行了讨论。一般情况下，建议设置半径为r=1。4.1中的实验表明图像片窗口越大，IPFCM的抗噪性就越强，但是边缘模糊现象就越明显。4.2和4.3中的实验显示，当图像片半径为时，无论合成图像还是MR脑图像，IPFCM都可以得到较高的分割精度，因此图像片半径为具有很强的适用性。

5.结论

本文提出一种全新的基于图像片进行模糊C均值聚类的图像分割理念与IPFCM方法，通过实验对比发现，IPFCM很好地克服了FCM分割方法对于噪声的敏感以及隶属度函数的非单峰值的缺陷，具有很好的抗噪性和较高的分割精度，图像的隶属度函数与理想隶属度函数十分接近。与同类方法相比，IPFCM不需要过多的参数设定，具有很好的鲁棒性和较强的可靠性。同时，本文将聚类中心的每一个成员扩展为一个向量，并给出了向量聚类中心的更新公式，为日后将多种图像特征加入FCM对图像进行分割提供了充分的理论基础。需要指出的是，本文采用正方形图像片，并未将图像像素点的方向信息考虑进去，使得图像细节部分容易被起周边像素影响而丢失信息。另一方面，当使用半径较大的图像片时，将会不可避免的降低分割精度，可以对分割后的图像进行二次聚类以提高分割精度。如何在图像片中加入方向信息，以及引入哪些图像特征将是未来研究工作的重点。

[1]JC Dunn.A fuzzy relative of the ISODATA process and its use in detecting compactwell separated cluster[J].Journal of Cybemet，3：32～57，1974.

[2]JC Bezdek.Pattern recognition w ith fuzzy objective function algorithms[M].Norwell，MA，USA：Kluwer Academ ic Publishers，1981.

[3]A.Buades，B.Coll，and J.-M.Morel.A non-local algorithm for image denoising [J]，Proc.IEEE Conf.Computer Vision and Pattern Recognition，vol.2，pp.60-65，Jun.2005.

[4]F.Hoppner，F.Klawonn.Improved fuzzy partitions for fuzzy regressionmodels[J]，Int.J.Approx.Reason.32(2)85–102，2003.

[5]MN Ahmed，SM Yamany，N Mohamed，AA Farag，Moriarty T.A modified fuzzy c-means algorithm for bias field estimation and segmentation ofMRIdata[J].IEEE TransMed Imag 21，193–199，2002.

[6]SChen，DQ Zhang.Robust image segmentation using FCM with spatial constraints based on new kernel-induced distancemeasure[J].IEEE Trans SystMan Cybern Part B 34，1907–1916，2004.

[7]L Szilágyi，Z Benyó，SM Szilágyi，HS Adam.MR brain image segmentation using an enhanced fuzzy c-means algorithm [J].Proc 25th Ann IntConf IEEEEMBS，2003：724–726.

[8]U Vovk，F Pernus，B Likar.A Review of Methods for Correction of Intensity Inhomogeneity in MRI[J].Medical Imaging，IEEE Transactions on Volume 26，Page(s)：405–421，March 2007.