微粒群优化的Canny边缘检测方法

陈燕龙

（广州航海高等专科学校信息与通讯工程学院，广东 广州 510725）

1.引言

图像的边缘是图像的最基本特征。边缘检测在图像分割、图像增强及图像压缩等领域中有着广泛的应用，而且一直是数字图像处理领域研究的热点和焦点问题。图像边缘蕴含了丰富的内在信息，主要划分为阶跃状和屋脊状两种类型。阶跃状边缘两侧的灰度值变化明显，屋脊状边缘则位于灰度增加与减少的交界处。传统的图像边缘检测方法大多是从图像的高频分量中提取边缘信息，微分运算是边缘检测与提取的主要手段。由于传统的边缘检测方法对噪声敏感，所以实际运用效果有一定的局限性。近年来，越来越多的新技术被引入到边缘检测方法中，如数学形态学、小波变换、神经网络和分形理论等。

Canny提出了最佳边缘检测算子即Canny算子[1]，得到了广泛的应用，并成了与其它实验结果作比较的标准。其原因在于他最先建立了优化边缘检测算子的理论基础，提出了迄今为止定义最为严格的边缘检测的三个标准。另外就是其相对简单的算法使得整个过程可以在较短的时间内实现。实验结果也表明，Canny算子在处理受加性高斯白噪声污染的图像方面获得了良好的效果[2]。

但是在应用Canny算子进行边缘检测时，对像素梯度进行模非极大值抑制后，要设定高、低2个阈值进行边缘筛选，这2个阈值的选取目前还没有统一的标准，对不同的图像缺乏自适应性，而且无法消除局部噪声干扰，在检测出伪边缘的同时还会丢失一些灰度值变化缓慢的局部边缘。本文在对传统Canny算法进行分析的基础上，提出了一种基于微粒群优化算法的Canny算法，针对不同图像自适应地生成动态阈值，取得了良好的检测精度和准确度。并与基于遗传算法进行优化的结果进行了比较。

2.Canny算法

2.1 最佳逼近函数

对一幅图像进行边缘检测，一般可分为三步：滤波、增强和检测。Canny算法也是一个具有类似步骤的多阶段的优化算法。Canny给出的评价边缘检测性能的3个指标如下：

(1)高信噪比准则。即输出信号的信噪比大，使得非边缘点或边缘判断为非边缘点的概率最小。信噪比(SNR)的数学表达式为

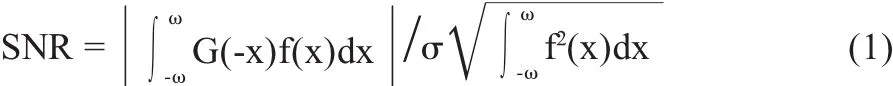
其中，f(x)是边界为[-ω，+ω]的滤波器脉冲响应；G(x)为边缘函数；σ为高斯噪声的均方根。信噪比越大，误检率越低。

(2)高定位精度准则。即检出的边缘点与实际边缘点距离最小，使定位精度最高。定位精度的数学表达式为

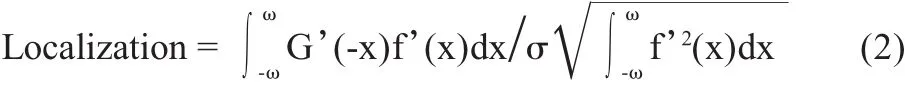
其中，G’(-x)和f’(x)分别为G(-x)和f(x)的一阶导数。Localization的值越大，定位精度越高。

(3)单一边缘响应准则。即和每个边缘有且只有一个响应，最大限度抑制伪边缘出现。要保证单一边缘响应，检测算子脉冲响应导数的零交叉点平均距离应满足

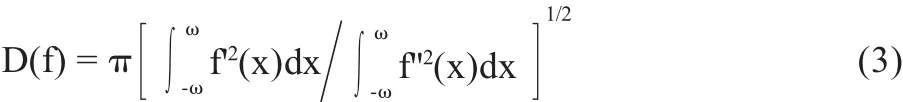
设高斯二维函数为

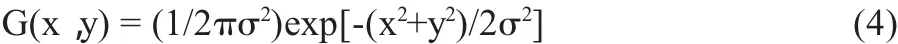
式(4)即为满足3个准则的最佳逼近函数。Canny以上述指标和准则为基础，利用泛函求导方法导出高斯函数的一阶导数，推导出最优边缘检测算子的一个近似实现：边界点位于图像被高斯函数平滑后的梯度幅度的极大值点。

2.2 实现过程

(1)平滑图像。利用式(5)所示的一维高斯函数对原始图像进行平滑除噪，从而得到平滑图像I(x，y)。

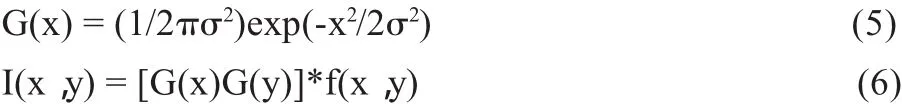
其中*表示卷积，f(x，y)是原始图像，σ是高斯函数的散布参数，用它控制平滑程度。

(2)计算梯度方向和幅值。采用2×2邻域一阶偏导的有限差分计算平滑后的图像I(x，y)的梯度方向和幅值：

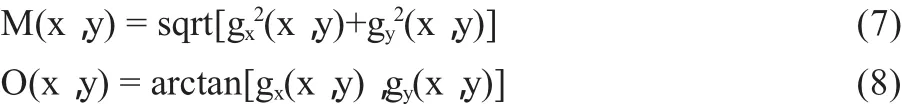
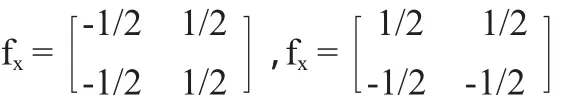
其中，gx和gy分别为原图像I(x，y)被滤波器fx和fy沿行、列作用的结果。

(3)对梯度图像进行非极大值抑制。若像素点(x，y)的梯度幅值M(x，y)不小于梯度方向上两个相邻像素点的梯度幅值，则判断该点为可能的边缘点[3]。

(4)双阈值方法检测和连接边缘。取两次阈值th1（低阈值）和th2（高阈值），对梯度图像进行双阈值化处理，可得到一个高阈值检测结果和低阈值检测结果，再在前者中连接边缘轮廓，连接到端点时，到后者寻找弱边缘点，弥补前者的边缘间隙。

3.微粒群优化算法

3.1 标准微粒群优化算法（PSO）

PSO算法是由Eberhart和Kennedy于1995年首次提出[3]一种进化计算技术（evolutionary computation）。类似其它进化类算法，PSO算法采用群体和进化的概念，根据个体的适应值大小进行操作。不同的是，PSO算法将每个个体看作是在n维搜索空间中的一个没有重量和体积的微粒，并在搜索空间中以一定的速度飞行。该速度是由个体飞行经验和群体的飞行经验进行动态调整，最终使所有微粒趋近全局最好位置。

在标准PSO算法中，一个包含有M个粒子的群体，每个微粒的维数为n，其中Xi=(xi1，xi2，…，xin)为微粒i的当前位置；Vi=(vi1，vi2，…，vin)为微粒i的当前速度向量；Pi=(pi1，pi2，…，pin)是微粒i的个体最好位置；Pg为所有微粒在当前的全体最好位置。标准PSO算法的进化公式如下：

其中，ω(t)是惯性因子，一般可以设为随进化而线性减少；t为当前进化代数；φ2是加速因子，通常在0～2间选取；μi～U(0，1)是两个相互独立的随机数。为了减少在进化过程中微粒离开搜索空间的可能性，可以给速度Vi限定一个范围Vi∈[Vmin，Vmax]。

为了要保证算法的收敛性，每个微粒必须要收敛于各自的Pi点，这是由微粒的追随性和微粒群的集聚性决定的。从动力学的角度来看，PSO算法中微粒的收敛过程是以Pi点为吸引子，随着速度的变小而不断地接近Pi点。因此在整个过程中，在Pi点处实际存在某种形式的吸引势能场吸引着微粒，这正是微粒能保持聚集性的原因。但是在标准PSO微粒群系统中，微粒的收敛是以轨道的形式实现的，且微粒的速度总是有限的，因此在搜索过程中微粒的搜索空间是一个有限的区域，不能覆盖整个可行的空间。所以标准PSO算法不能保证以概率1收敛到全局最优解，甚至不能收敛到局部最优解，这正是其最大的缺点，所以许多学者对标准算法的改进进行了很多的探索。

3.2 基于量子行为的微粒群优化算法（QPSO）

量子化的微粒群算法[4，5]是从量子力学的角度对标准PSO算法的继承和推广。在QPSO中，微粒群按下面三个公式移动：

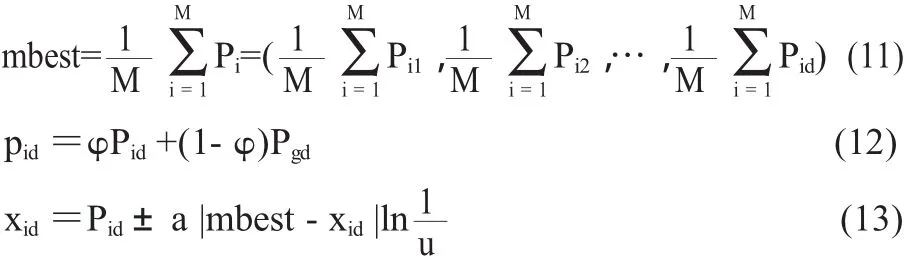
其中：φ，u=rand，mbest是微粒群的平均最优位置，pid为Pid和Pgd之间的随机点；a为QPSO的收缩扩张系数，它是QPSO算法收敛性的重要参数，取值方法为

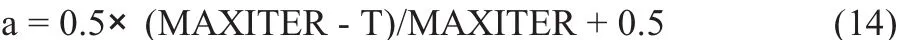
其中MAXITER是迭代的最大次数，具体a取值视情况而定；T为当前迭代次数。

PSO和QPSO的区别在于进化的方法不同，即更新微粒位置的方法不同。在PSO算法中，微粒必须在一个有限的搜索范围内以确保微粒群的聚集性，使算法收敛于一个最优点或局部最优点。而在QPSO算法中，微粒能以某一确定的概率出现在整个可行的搜索空间中任意一个位置。而这样的位置可能比当前群体中的个体极值具有更好的适应值，所以QPSO算法能较好地克服标准PSO算法在收敛性能上的不足。

4.基于微粒群优化算法的Canny边缘检测

4.1 平滑后对图像作灰度拉伸

对图像进行平滑，除噪的同时也会使灰度的变化范围变窄，一些边缘变得比较平缓，从而在后续的边缘检测中容易丢失边缘。为改变这种情况，在平滑后，对图像做灰度拉伸，增大图像的灰度分布的动态变换范围，增强对比度和边缘灰度的变换速率。

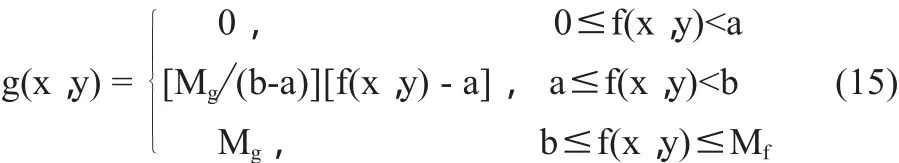
其中，对于灰度级为256的图像来说，Mg=Mf=255。a、b为常数，不同情况下灰度拉伸的a、b的取值要根据具体的条件进行选择。

4.2 微粒群优化算法求取阈值

从Canny算子的原理可以看出，影响算法性能的两个重要因素是σ和阈值Hth、Lth的选取。对于灰度平坦的图像，用较小的σ可以取得很好的平滑效果，但如果图象复杂度增加，σ也要有相应的增加。这会导致高斯平滑模板相应的增大，平滑的速度也大幅度变慢。本文实验中，σ取固定值1。

一幅在光照条件不好的情况下拍摄的图像，很可能会出现灰度分布的不均匀。这时，如果选择高阈值的Canny算子进行检测，图像的某些部分会丢失边缘；而选择低阈值Canny算子进行检测，又会出现很多虚假的边缘。可见，虽然双阈值法使Canny算子提取的边缘更具有鲁棒性，但阈值的选择对结果影响很大，而对不同的图像确定不同的阈值又较困难。

本文采用基于量子行为的微粒群优化算法（QPSO）选代求取最优阈值，作为Canny算子的高阈值Hth，对于低阈值的选择，通过选择为高阈值的一定比例因子实现，一般取Lth＝k Hth，其中比例因子k取1.5～2.5。

基于实时性的考虑，我们选取的适应度函数是最大类间方差的计算函数。计算公式为：

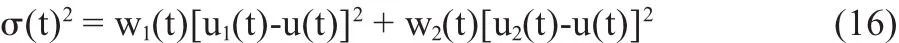
其中t表示用来处理图像的阈值，w1(t)表示图像中灰度值小于阈值的像素的总和，w2(t)表示表示图像中灰度值大于阈值的像素的总和，u1(t)表示图像中灰度值小于t的像素的平均灰度值，u2(t)表示图像中灰度值大于t的像素的平均灰度值，u(t)为目标图像的灰度均值。通过QPSO算法，找出使得σ (t)2最大的t的值，作为Canny算法的高阈值。算法流程如下：

(1)迭代次数t=0，对种群的每个粒子的位置向量进行初始化；

(2)根据目标函数计算每个粒子的目标函数值；

(3)更新每个粒子的新局部最优位置Pij；

(4)更新全局最优位置Pgj；

(5)根据(3)式计算mbest；

(6)根据(4)式计算每个粒子随机点pid；

(7)根据式(5)更新每个粒子的新位置；

(8)判断参数估计是否达到预定迭代步数或预定精度，条件满足则终止。否则，t＝t+1，返回(2)。

5.仿真结果

为了验证算法的结果，将本文算法与传统的Canny算法进行了实验对比。结果见图1。

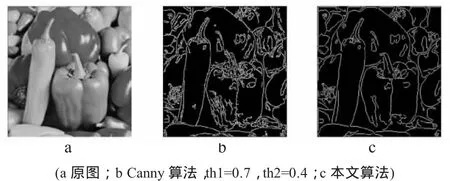
图1 仿真实验结果

实验中还采用检测图像的品质系数[6]R来评估算法的性能：

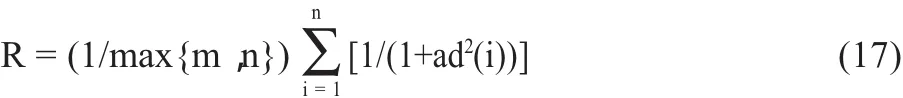
其中，m是真实边缘数；n是检测出的边缘数；d(i)表示第i条边缘与响应的检测边缘的距离，a为比例常数，可取为0.1，当R=1时是检测的理想状况。结果见表1。

从图1可以看出，传统Canny算法存在一些假边缘，同时丢失了一些真边缘。而本文算法不需要事先设定阈值，优化产生的阈值使得检测准确性得到较大的提高，边缘完整，定位准确，能够更好地保留边界和图像细节。从表1可以看出，本文算法所得边缘图像的品质系数明显高于传统Canny方法。

表1 图1中边缘图像的品质系数

与采用标准微粒群算法（PSO）和遗传算法（GA）进行选代求取最优阈值的结果进行对比发现，PSO没有遗传操作，其计算复杂度比GA低，QPSO的优势在于简单容易实现并且没有许多参数需要调整，收敛的速度快。比较结果见表2。

表2 迭代次数比较

6.结论

本文采用改进的微粒群优化算法对传统的Canny算法进行了改进，改善了对差分背景的图像边缘检测的效果，通过微粒群优化算法产生的阈值适应性好，自动化程度高。因为QPSO算法迭代次数少，算法的开销不大，显著提高了阈值选取的速度。虽然算法的运算复杂度和运算时间要稍大于普通的Canny算子，但优于采用遗传算法进行优化的情况，对实时性无明显影响。

[1]Canny J，A Computational Approach to Edge Detection[J].IEEE Transon PAM I，1986，8(6)：679-698.

[2]Zhang Bin，He Sai-xian.Improved Edge-detection Method Based on Canny algorithm[J].Infrared Technology，2006 28(3)：165-169.

[3]Kennedy J，Eberhart R.Particle Swarm Optimization[C].Proceedings of IEEE IntConf on Network，1995：1942-1948.

[4]SUN Jun，XUWenbo.A global search strategy of quantum-behaved particle swarm optim ization：proc.Of IEEE Conference on Cybernetics and Intelligent Systems[C].Singapore：[s.n.]，2004：111-116.

[5]SUN Jun，FENG Bin，XU Wenbo.Particle swarm optim ization w ith particles having quantum behavior：proc of Congress on Evolutionary Computation，2004：325-331.

[6]William K.Pratt数字图像处理[M].邓鲁华，张延恒等译.北京：机械工业出版社，2005：330-332.