基于MATLAB及参数化建模的起重机桁架式臂架结构优化设计

张 欢 徐长生

(武汉理工大学物流工程学院 武汉 430063)

由于大型起重机桁架式臂架的弦杆一般采用费用较高的高强度钢管,故针对减少臂架自重的优化设计的重要性十分明显.在起重机桁架式臂架的优化问题中,由于设计变量多、优化约束条件复杂并且为非线性状态,使得优化的难度有所增加.针对这种典型的非线性规划问题,本文采用了MAT LAB优化工具箱中的遗传算法工具箱及fmincon优化函数,以便能高效地求解出全局的最优解.在得出优化后的设计变量后,将变量赋给用APDL语言编写好的ANSYS臂架模型文件,进行计算后能直接观察出应力分布情况以验证优化的正确性.

本文以300 t-48 m船用甲板起重机的桁架式臂架为实例研究对象,通过以上优化方法和参数化建模,确定最优解,对快速确定设计方案以及降低制造成本有一定指导意义.

1 起重机桁架式臂架结构优化设计数学模型

1.1 臂架优化数学模型的设计变量

针对桁架式的单臂架,为了有效地表达整个桁架系统的几何要素,采用7个设计变量.X= (A,B,D1,d1,t,D2,d2),其中：A为臂架高度;B为臂架宽度;为主弦杆外径;为主弦杆内径;t为腹杆节间距;为腹杆外径为腹杆内径.

变量所指代的各几何要素具体位置以及臂架外观可见图1、图2.

图1 臂架结构设计变量示意图

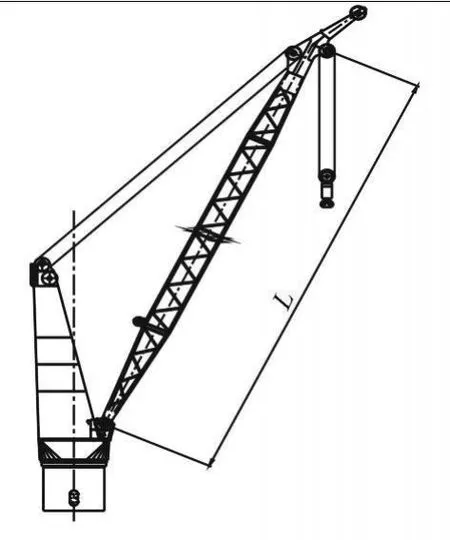
图2 300t-48m船用甲板起重机整机

1.2 目标函数

优化设计的目标函数F(X)为臂架桁架部分的重量,其计算式为

式中：L为臂架桁架部分总的长度;ρ为钢材密度,均为初始设计参数.需要说明的是,一般此类桁架式臂架的两端比中间要略窄,且臂架头部、根部的腹杆体系会有所加强,但为了简化设计变量,此目标函数做了一定的简化处理,所以其值和实际臂架的桁架部分重量会有细微差别,但对于在优化设计中比较各种方案的适应度以找到最优点几乎是没有影响的.

1.3 约束函数

以目前设计要求而建立起来的约束条件主要包括臂架强度、刚度、总体稳定性、局部稳定性以及腹杆体系约束等[1].

1)臂架强度约束

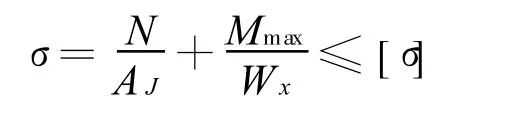
式中：AJ为臂架截面静面积;Mmax为臂架所受最大弯矩;为臂架变幅平面内的抗弯截面模量; [σ]为臂架许用应力.

2)臂架刚度约束[2]

式中：f为臂端挠度;N为臂架轴向压力;β为臂架下铰点与回转中心线的距离l1与臂架下绞点与吊钩中心水平距离l2的比值;a为等于为臂架变幅平面内的惯性矩;T为臂架侧向集中力;L为臂架长度;[f]为臂端容许挠度,规范规定[f]=0.7L2.

3)臂架总体稳定性约束[3]

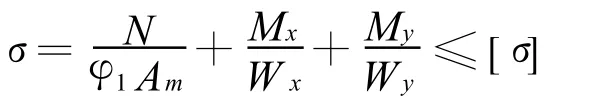
4)弦杆节间稳定性约束[4]

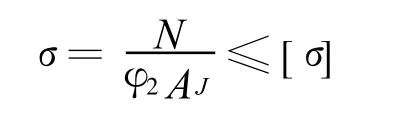
5)腹杆体系长细比约束

综上,共5组性能约束,均为非线性约束.

2 优化方法

借助MATLAB优化工具箱采用了遗传算法和fmincon函数求解两种优化方法进行优化设计.遗传算法是通过模仿生物进化过程求解非线性、多模型、多目标等复杂系统优化问题的通用框架[5].是以二进制的形式来表示各个变量,并将不同的变量组合转化为类似生物体基因组合的形式,通过选择、交叉和变异这三个基本操作,来计算每代种群的适应值,即目标函数值,不断剔除不适应的解,进而寻找到最优解[6].

而fmincon函数是MATLAB优化工具箱中专用于求解带约束的优化问题的.计算非线性规划问题时速度较快,但容易陷入局部最优.这里选用两种优化方法,主要是为了通过对比更好地找到全局最优解.

3 参数化建模

利用ANSYS有限元计算软件所支持的APDL参数化语言对臂架进行参数化的建模,以方便对种优化方案进行分析.APDL文件中涉及到参数的部分建模语句如下.

4 优化计算实例

以300 t-48 m船用甲板起重机的桁架式臂架为优化实例,首先进行基于遗传算法的优化,定义用来限定各变量之间的线性关系的线性约束条件都为矩阵.本例中是用于限定主弦杆及腹杆壁厚范围,这样的线性约束有助于尽早排除不合理的优化方案,提高了求解效率.根据经验可确定：

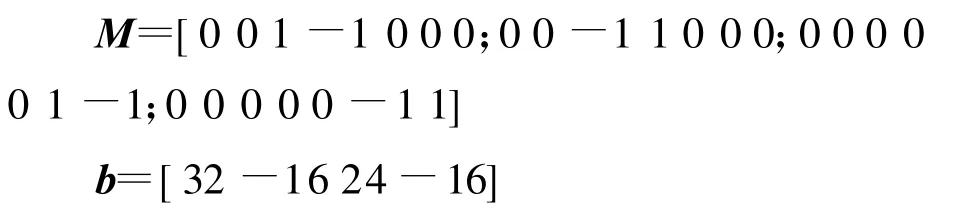
即规定主弦杆壁厚为8～16 mm,腹杆壁厚为8～12 mm.

其次根据经验定义7个变量各自的区间范围矩阵Alb和Aub：

从而限定了优化过程中各变量的变化范围.最后定义非线性约束函数即前面归纳的五组性能约束,钢材材料为Q345B,σs=345 MPa,安全系数取1.5,[σ]=σs/1.5=230 MPa,[λ]=150,将其编写进入MAT LAB的M文件直接调用即可.

经过计算,在初始种群数为 40,交叉概率0.8,变异概率0.2,罚函数因子100的情况下,进化到200代时目标函数取得了最优值.相对应的最优解各变量数值如图3,种群寻优进化时对应的函数值曲线如图4.

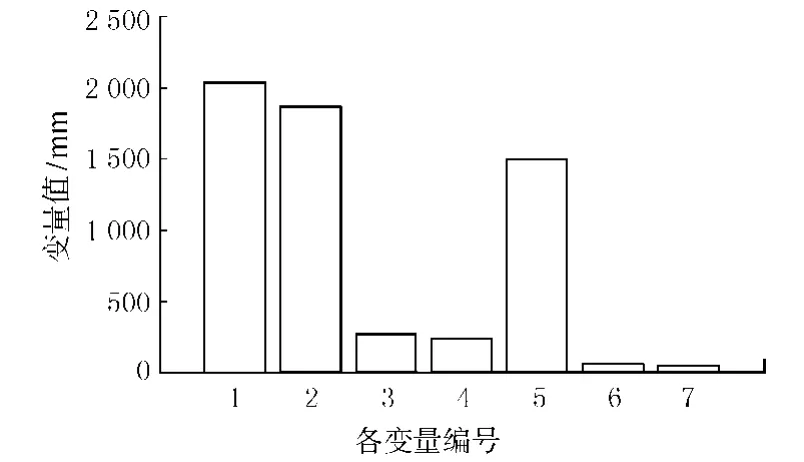
图3 最优解时各变量数值图

采用fmincon函数求解时线性约束条件、区间范围、非线性约束条件都与用遗传算法计算时一样,在迭代到42代时找到最优解,如图5.

图4 种群代数-目标函数值图

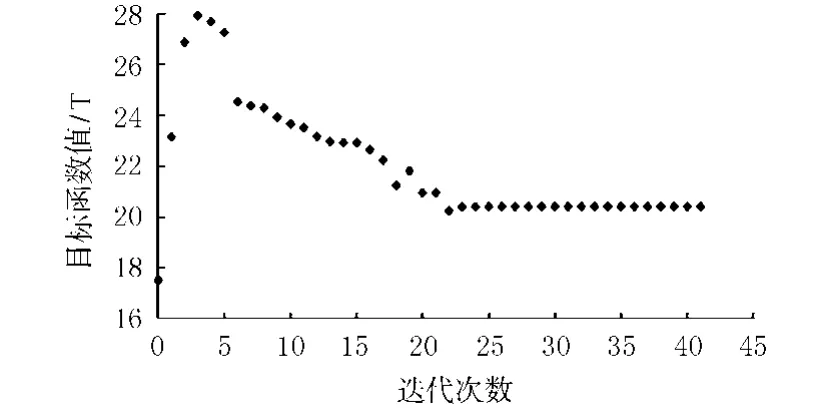
图5 迭代次数-目标函数值图

经过对上述两种优化方法求出的最优解比较,发现应用fmincon函数求解本数学模型时速度较遗传算法更快且结果更加优化,故采用该组优化数据和原设计方案的相关变量进行了分析对比,对比结果如表1所列.

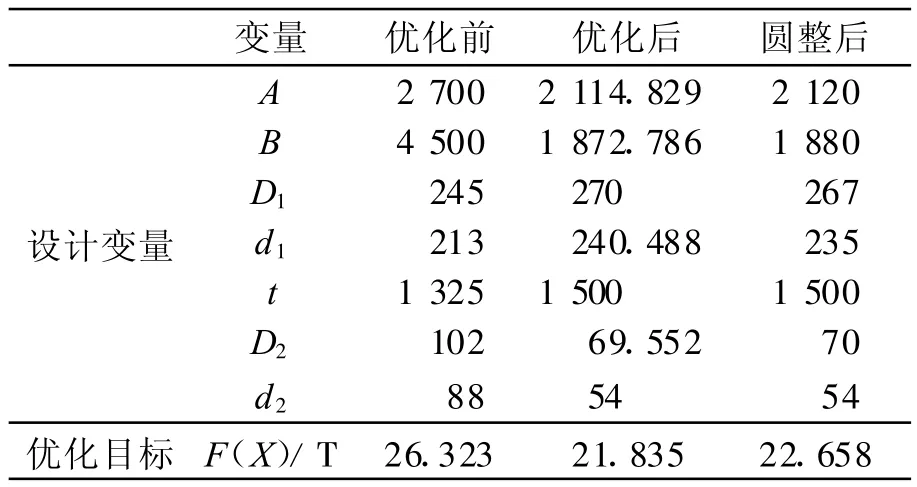
表1 优化结果对比 mm

可见优化后臂架桁架部分减轻了约3.7 t.将优化设计所得出的变量值赋给APDL文件导出ANAYS模型应力图如图6,结构最大应力为190 MPa,小于[σ],验证了该优化设计的正确性.

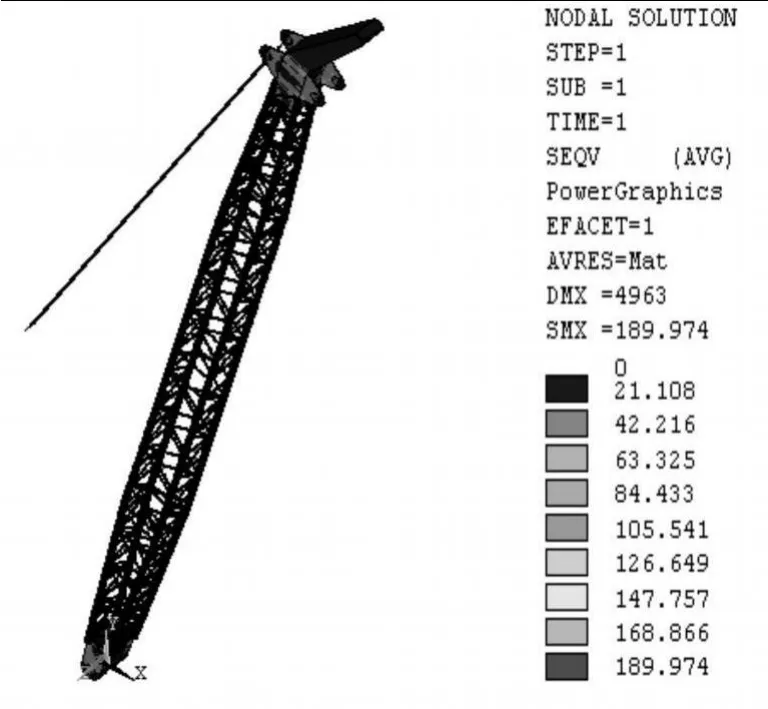
图6 臂架结构模型应力图

5 结束语

本文采用了遗传算法和fmincon函数求解两种优化方法,并根据桁架式臂架的结构特点进行优化,相对于其他的优化算法更为接近全局最优,并且结合APDL参数化建模语言实现了根据不同优化方案自动建模,使整个设计过程快捷、可靠.优化结果减轻了臂架的重量,降低了制造成本,同时也满足了安全性的要求,具有较好实际应用价值.

[1]苏文力,徐长生.基于一阶优化方法的桥式起重机结构有限元分析[J].武汉理工大学学报：交通科学与工程版,2006,30(4)：619-622.

[2]王金诺,于兰峰.起重运输机金属结构[M].北京：中国铁道出版社,2002.

[3]上海港机重工有限公司.港口起重机设计规范[S].北京：人民交通出版社,2007.

[4]陈玮璋.起重机械金属结构[M].北京：人民交通出版社,1986.

[5]龚 纯,王正林.精通M ATLAB最优化计算.北京：电子工业出版社,2009.

[6]陈 昆.基于改进遗传算法的起重机臂架结构优化设计[J].武汉理工大学学报：信息与管理工程版, 2009,31(5)：748-751.