离散变量结构形状优化设计的混合遗传算法*
朱朝艳 张延年 郭鹏飞 王学志
(辽宁工业大学土木建筑学院1) 锦州 121001) (沈阳建筑大学土木工程学院2) 沈阳 110168)
0 引 言
结构形状优化设计需求解两类变量即截面尺寸变量,与描述结构几何外形的形状设计变量,不仅设计变量的数目增多,而且截面变量与形状变量对目标函数和约束函数而言具有不同的非线性性质,两者的量纲、量级通常也不同,两类变量的耦合可能导致收敛上的困难.对于离散变量结构问题,由于截面面积只能取离散值,因此问题就成为一个非线性混合离散变量优化问题,求解起来更为困难.传统的形状优化设计一般采用分层优化方法[1-3],虽然使用有效且易于操作,但由于分层优化导致变量空间上的分割,可能带来的后果是解空间可行域的缩小,这样有可能丢失真正的最优解.近年来,将两类变量综合考虑的形状优化设计方法越来越引起人们的关注,并成为研究热点,但迄今为止,成果不多,离散变量问题这方面的成果更少,在国内对此有突出贡献的是孙焕纯和石连栓[4-5].本文用拟满应力遗传算法来解决离散变量结构的形状优化问题,取得了较为满意的结果.
1 离散变量结构形状优化设计问题的数学模型
离散变量结构形状优化设计问题的设计变量为杆件的截面积和节点坐标,目标函数一般为结构的总体重量,约束条件为应力约束、节点的位移约束、稳定约束和动态约束等.
以杆系结构受应力和位移约束的形状优化问题为例,数学模型可表达为
求A,X
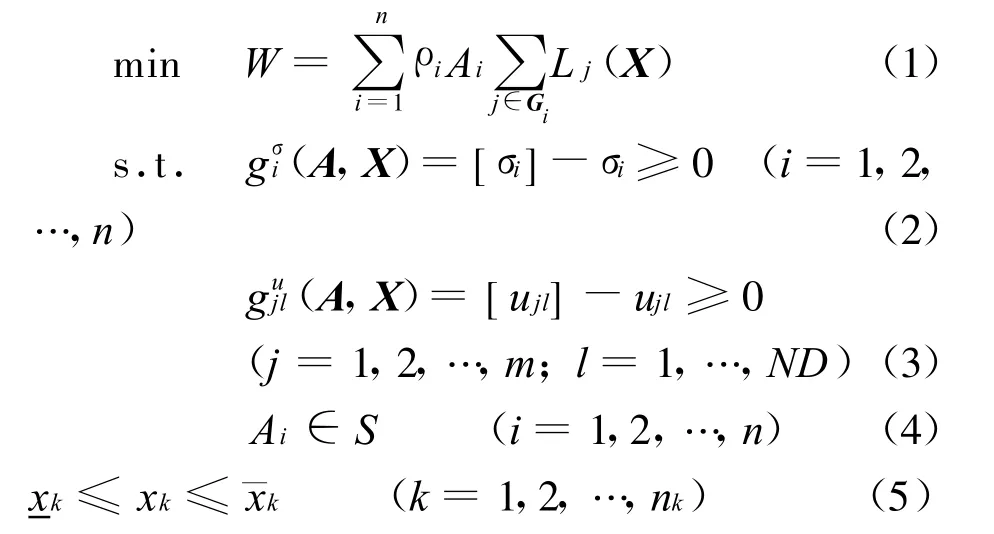
2 拟满应力遗传算法
标准遗传算法在结构优化设计中存在计算量大、收敛进程慢以及容易陷入局部最优解等问题,而拟满应力方法迭代次数少,容易收敛,具有很强的局部寻优能力.本文将拟满应力算法与遗传算法相结合,在遗传算法中嵌入拟满应力算子,与标准遗传算子共同构成一种混合遗传算法——拟满应力遗传算法.同时还采用最优个体保留、最差个体替换和控制种群个体差异等改进措施[6].这种混合遗传算法结合了两种算法的优点,它克服了拟满应力法解决问题的局限性,又比标准遗传算法更加快速有效.
拟满应力遗传算法的步骤如下.
1)进化代数计数器初始化:k=0.
2)随机产生初始种群P(k).
3)评价种群P(k)的适应度.
4)选择群体中2个个体以概率Pc进行交叉操作:P′(k),←Crossover[P(k)].
5)对子代群体中每个个体以概率Pm进行变异操作:P″(k),←Mutation[P′(k)].
6)对子代群体中每个个体以概率Ph进行拟满应力操作:P‴(k),←Full-stress[P″(k)].7)评价群体P‴(k)的适应度.
8)个体选择、复制操作:P(k+1)←Rrproduction[P(k)∪P‴(k)].
9)将该代中最优个体与该代前最优个体比较,并用比较后的最优个体替换该代中最差个体,直接进入下一代进化.
10)进化终止条件判断:若不满足进化终止条件,则:k←k+1,转到第3)步,继续进化过程;若满足进化终止条件,则输出最优个体.
3 基于拟满应力遗传算法的形状优化设计方法
3.1 两类变量的耦合方法
将形状变量和截面变量分开考虑可降低求解的难度但并不能保证得到全局最优解,只有将两类变量综合考虑才是解决问题的有效办法.但是将两类变量统一考虑,可能由于两者的量纲和优化过程中量级的不同而导致算法收敛上的困难,甚至发散.为了解决两类变量间的耦合问题,本文采用的方法是将形状变量和截面变量编码表示在同一个染色体中,这样两类变量在遗传算法中被统一表示成位串形式.由于遗传算法的操作对象是变量编码后的位串,并且对问题的要求仅仅是能求出非负的适应度值,遗传算法就可以以适应度值为依据指导搜索,从而找到全局最优解.
3.2 两类变量统一表示的编码和解码方法
用一定长度的二进制染色体代表一个设计变量,多个染色体首尾连接构成设计变量空间.这种编码方法,容易处理设计变量为离散/连续混合的结构形状优化问题.
设形状变量个数为n1,每个变量的二进制子串长度为m1,截面变量个数为n2,每个变量的二进制子串长度为m2,则形状变量位串总长度为n1◦m1,截面变量位串总长度为n2◦m2,再将表示形状变量的n1个m1位的子串和表示截面变量的n2个m2位的子串首尾相连,即形成一个染色体,它可以表示一个个体.编码方法如图1所示,图中“*”为通配符,代表1或0.
解码时,将表示一个个体的二进制染色体串按照形状变量和截面变量的位串总长度分成两个部分,然后再将表示形状变量的位串分成n1段,每一段表示n1个形状变量中的一个变量;将表示截面变量的位串分成n2段,每一段表示n2个截面变量中的一个变量.然后根据二进制位串与十进制数的对应关系可得出十进制数,并对应地映射到变量的离散值或连续值.

图1 编码方法示意图
3.3 优化策略
本文主要解决离散变量的结构优化问题,因此比较适合用二进制编码表示.但形状变量可以是连续变量,也可以是离散变量.当形状变量是离散变量时,优化问题依然为离散变量问题,而当形状变量是连续变量时,则优化问题为混合离散变量问题.此时二进制编码的长度直接影响连续变量的求解精度,若想提高解的精度必须采用较长的编码,这必然会影响求解的效率.若将形状变量用实数码表示,而截面变量用二进制码表示,则在解码和交叉、变异等操作上处理起来又过于繁琐,基于此,本文对两类变量仍采用二进制编码.为了解决搜索效率问题,对形状变量采用二级编码方法对应二级搜索,首先采用一个较短的编码在整个搜索空间进行粗粒度搜索,由于遗传算法有很好的全局搜索性,可以很快搜索到最优点附近,然后再在最优点的附近区间重新编码,继续进行细致搜索.采用这种二级处理方法,由于在整个搜索过程中形状变量的子串都不长,可以显著地减小搜索空间,因而可以在很大程度上加快搜索进程.
4 优化算例
例1 37杆桁架简支桥
该例题选自文献[7].桁架简支桥结构受均布载荷作用.初始设计见图2,截面积均为8 cm2.假设结构下弦节点固定不动,节点载荷P=10 kN.上弦节点可沿垂直方向移动.节点10的垂直位移受到约束,要求小于l cm(跨度的1/1 000).结构对称性保持不变,最小截面积为0.5 cm2.材料弹性模量E=210 GPa,密度ρ=7 800 kg/m3,全部杆件的许用应力均为240 MPa.
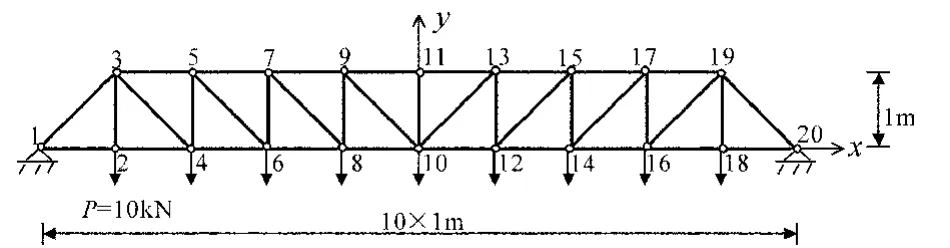
图2 桁架桥结构
原题为连续变量优化问题,要求最小截面积为0.5 cm2,本文从标准型钢表中选取29个数值,各杆截面积离散集为S={0.503,0.636, 0.785,0.950,1.131,1.327,1.539,1.767,2.011, 2.270,2.545,2.835,3.142,3.464,3.801,4.155, 4.524,4.909,5.309,5.726,6.158,6.605,7.069, 7.548,8.042,8.553,9.079,9.621,10.18}cm2.
考虑结构对称性要求,将截面设计变量分成19组,将坐标设计变量分成5组,分组情况表1所列.标准遗传算法、拟满应力遗传算法的优化结果见表2所列,约束条件均满足要求.

表1 桁架桥变量连接情况
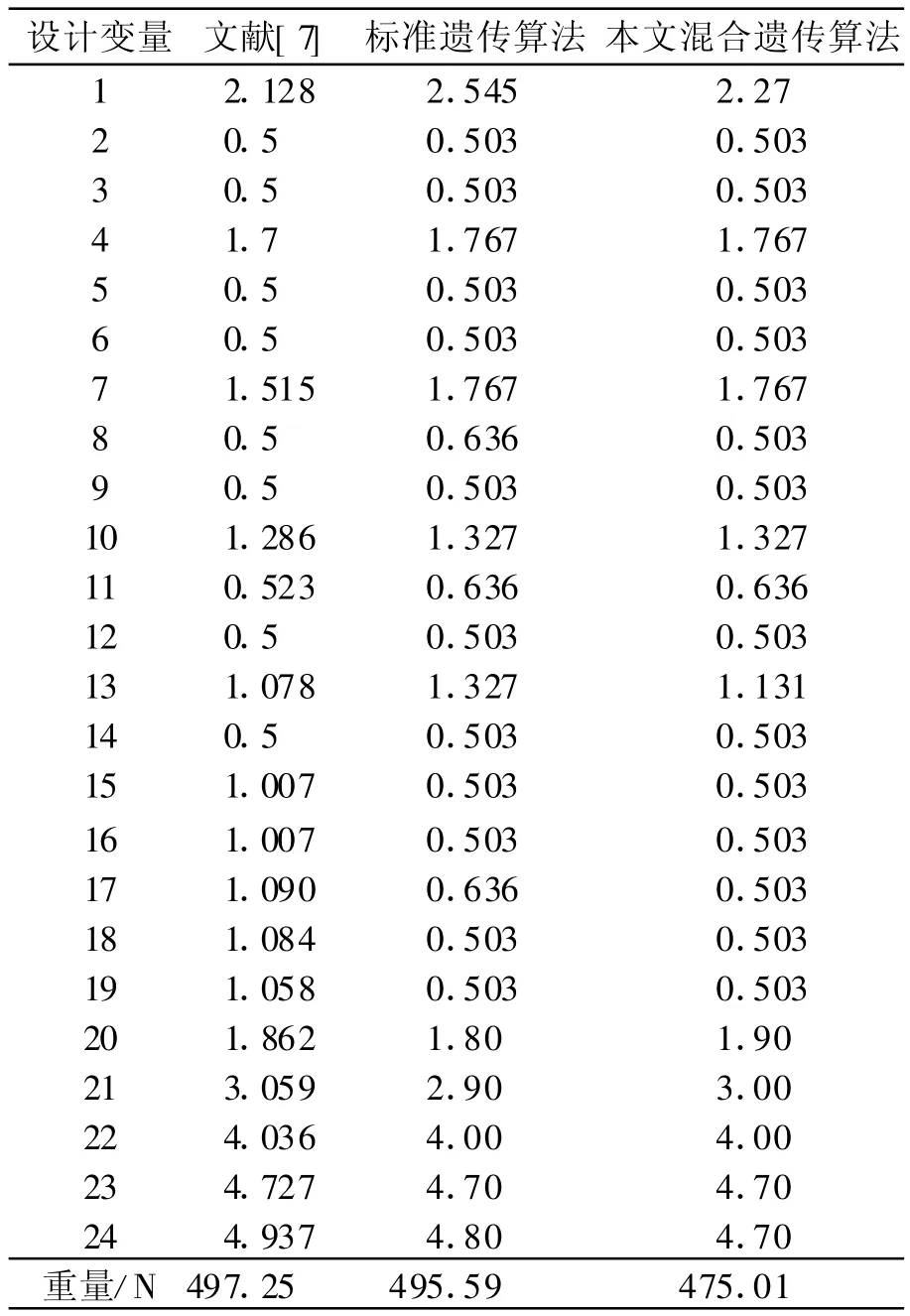
表2 桁架桥优化结果 m
从表2可以看出,本文采用的方法与标准遗传算法相比,重量下降了4.15%;和文献[7]优化后的结果相比,重量减轻了4.47%.再与文献[7]的初始设计比较,文献[7]的初始设计结构重量为256.73,即25 159.54 N,拟满应力遗传算法形状优化后重量为475.01 N,重量较文献[7]的初始设计降低了81.12%,可见用本文采用的基于拟满应力遗传算法的将两类变量综合考虑的形状优化设计的效果是十分明显的.
5 结束语
本文将拟满应力遗传算法应用于离散变量结构形状优化问题.将形状设计变量和截面设计变量综合考虑,同时采用二级搜索策略减少整个搜索过程中形状变量的搜索空间,进而加快搜索进程.通过算例表明,本文的优化策略和优化算法是可行和有效的.
[1]隋允康,由 衷.具有两类变量的空间桁架分层优化方法[J].计算结构力学及其应用,1990,7(4):82-92.
[2]Salajegheh E,Vanderplaats G N.Optimum design of trusses with sizing and shape variables[J].Struct. Opt.,1993(6):79-85.
[3]隋允康,高 峰,龙连春.基于层次分解方法的桁架结构形状优化[J].计算力学学报,2006,23(l):46-51.
[4]石连拴,孙焕纯,柴 山.两类变量综合处理的结构形状优化设计方法[J].计算力学学报,1999,16(4):416-420.
[5]石连拴,孙焕纯.离散变量结构形状优化设计的综合算法[J].力学学报,1999,31(6):731-737.
[6]朱朝艳,刘 斌,郭鹏飞.离散变量桁架结构拓扑优化的混合遗传算法[J].机械强度,2004,26(6):656-661.
[7]王 栋,张卫红,姜节胜.桁架结构形状与尺寸组合优化[J].应用力学学报,2002,19(3):72-76.

