一种基于Radon变换的SAR多普勒参数估计方法

朱振波 陈风波 汤子跃

(空军雷达学院空天基系 武汉 430019)

在SAR成像中,只有采用精确的多普勒参数,才能得到高质量的SAR图像.如果在成像处理时采用的多普勒中心频率和多普勒调频率带有误差,将会降低参考函数或补偿因子的精确性,进而影响图像质量.多普勒中心频率误差将使图像的信噪比和信号模糊度下降,并使图像产生位置偏移,多普勒调频率估计误差将造成图像散焦和模糊不清,可见多普勒参数估计是SAR精确成像处理的重要组成部分.通常,从回波数据估计多普勒中心频率的算法称为杂波锁定,估计多普勒调频斜率关称为自动聚焦.对多普勒中心频率进行估计,通常用的是谱域相关估计法,包括多普勒频谱分析法、能量均衡法、时域相关法等.这些方法都是用回波信号的方位谱来估计多普勒中心频率,当成像景物为均匀背景时,它们将得到好的结果,当成像景物有只通过部分波束的强散射点,它将造成平均功率谱的扭曲,进而影响多普勒中心频率的估计,而且存在多普勒模糊的问题[1-3].

本文分析了SAR方位向多普勒参数与其工作几何结构的关系,基于此提出了利用Radon变换实现SAR多普勒参数估计的方法.通过选择适当的数据窗口大小,该方法能够准确地估计出实时多普勒中心和多普勒调频率,且该方法避免了其他多普勒中心估计方法中的多普勒模糊问题,它是一种可行的基于回波数据的SAR多普勒参数估计方法,最后给出了相应的计算机仿真.

1 SAR信号模型

SAR系统的模式通常有3种：条带式、扫描式和聚束式.条带式成像的SAR可以采用正侧视(收发波束指向与其平台运动方向垂直),也可以采用斜侧视(收发波束指向与其平台运动方向有一定夹角)的工作方式,图1给出了正侧视模式时的几何结构示意图.图中实线航迹表示存在运动误差时的实际航迹路线;载机平台到测绘中心Pn的正侧视距离为为载机高度.定义为到目标P的收发距离和,在不考虑幅度调制的条件下,接收信号可表示为

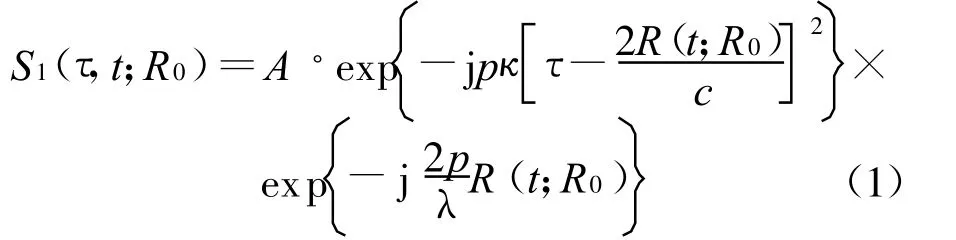
式中：c为光速;κ为发射信号调频斜率;λ为波长;τ为快时间;t为慢时间.

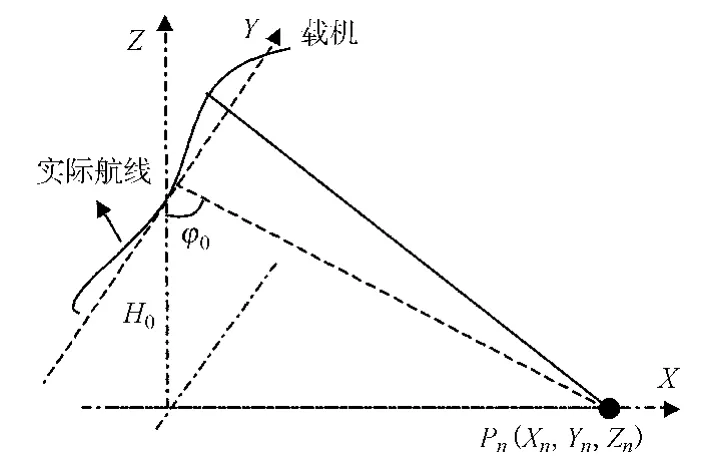
图1 SAR工作模型

2 SAR多普勒参数估计

2.1 多普勒参数与SAR工作几何结构的关系

图1中的虚线航迹是正侧视SAR理想工作时的航迹,实际工作中,由于多种因素的影响,实际航迹会偏离理想航迹,如图1中的实线航迹所示,这时对应的SAR多普勒参数也发生改变,为了获得高质量的SAR图像,必须采用准确的多普勒参数估计值.

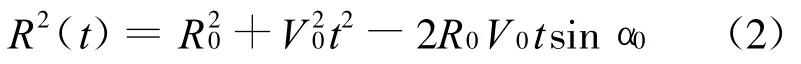
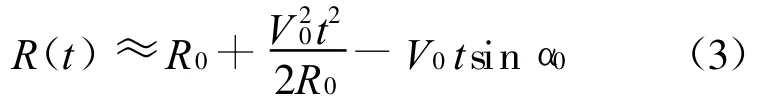
由式(3)可以求得t时刻方位向多普勒频率f(t)为

由式(4)可以得到多普勒参数为

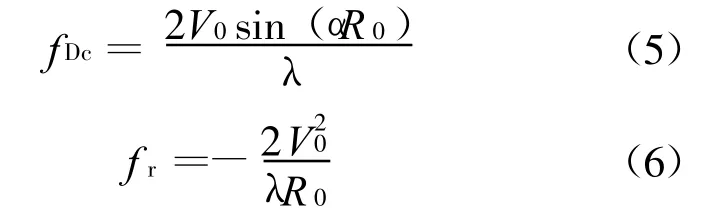
将式(5),(6)代入式(3)得到SAR收发距离和为

同时,对成像区域中某个给定的距离单元,在合成孔径成像时间内,其多普勒频率是线性的,因此可利用时频技术估计该线性调频信号的调频率.

2.2 Radon变换原理

Radon变换是通过直线积分将以一个二维平面转换为另一个二维平面,它可以用来检测二维平面上的直线分量[5].平面S上二维Radon变换的定义为

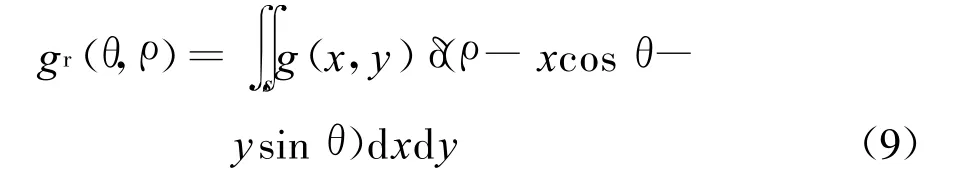
式中：S为整个x-y平面;g(x,y)为平面上点(x, y)的幅值;δ(α)为狄拉克函数.如图2,由于δ(α)的作用,Radon变换沿着直线y=ax+b进行.式中为二维平面S的原点到直线y=ax+b的距离为横坐标到直线的法线的夹角.通过积分作用,直线y= ax+b被映射到ρ-θ平面内的一个点.因此,基于Radon变换可以实现二维平面上直线特征的提取.

图2 Radon变换原理示意图

2.3 多普勒中心估计

由前面的分析可知,距离走动分量是线性的,只要能够获取选定的SAR回波数据的距离走动斜率 ,就可以得到该数据段的多普勒中心估计值.基于Radon变换可以实现二维平面上直线特征的提取,因此对距离压缩后的数据平面进行Radon变换,可以提取所选数据段的距离压缩曲线的距离走动斜率,然后根据式(8)可以得到多普勒中心的估计值,这种多普勒中心的估计方法,可以获得实时的多普勒中心估计值,且避免了常规方法中的多普勒模糊问题[6-8].

基于Radon变换的多普勒中心估计方法详细流程如下.

1)进行原始回波数据的距离压缩处理.

2)定义窗大小,从距离压缩后的成像平面上截取待估计的数据平面S.

3)求所选数据平面S上每个像素点的幅度,得到二维幅值平面.

4)将二维幅值平面S1的横纵坐标的变换到“s-m”,然后进行Radon变换,将映射到ρ-θ平面,得到

6)在一维平面d(θ)上,进行归一化处理,并计算峰值所对应的θe值.

7)计算实际的距离走动斜率κr=tan θe.

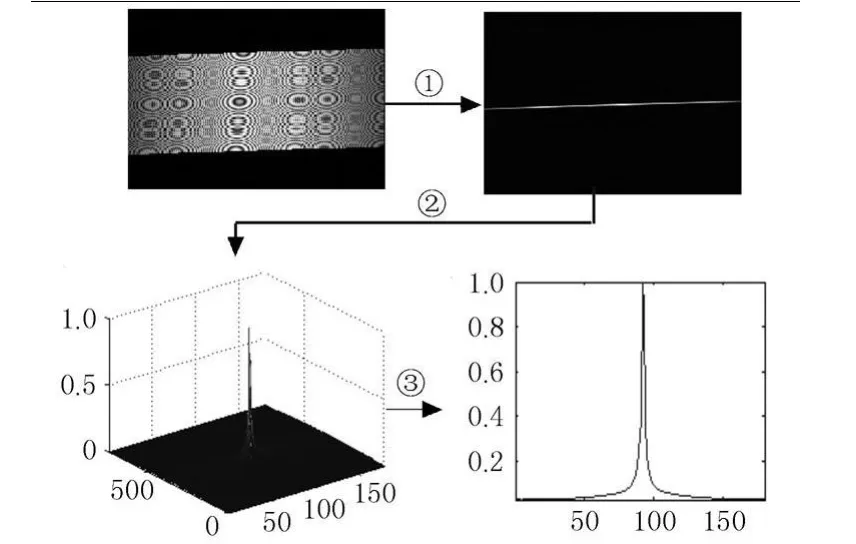
图3 基于Radon变换的多普勒中心估计示意图

2.4 多普勒调频率估计

对成像区域中某个给定的距离单元,在合成孔径成像时间内,其多普勒频率是线性的,且在一定聚焦深度内的子测绘带,可以选用相同的多普勒调频率.因此,对选取的某一距离单元的回波信号,可以利用 Wigner-Radon变换估计该距离单元处的多普勒调频率.

基于Wigner-Radon变换的多普勒调频率的估计方法流程如下.

1)进行原始回波数据的距离压缩处理.

2)根据估计的多普勒中心值完成距离走动校正.

3)选取某距离单元的回波数据,进行Wigner变换,得到二维“时间-频率”平面S.

4)对二维幅值平面S进行Radon变换,将S平面映射到ρ-θ平面,得到

6)在一维平面d(θ)上,进行归一化处理,并计算峰值所对应的值,得到多普勒调频率的估计值

7)在该子测绘带中心两侧附近,对称选择n个距离单元,分别按照步骤1)～6)分别得到相应距离单元的多普勒调频率估计值 frn=tan θen.

8)计算多普勒调频率估计值 frn的方差值σfn,去除方差较大的 frn,将剩下的多普勒调频率估计值求平均,将其平均值作为最终的多普勒调频率的估计值.

图4给出了基于Wigner-Radon变换的多普勒调频率估计的主要流程示意图.图中：①是对选取的某距离单元回波数据进行Wigner-ille变换;②对Wigner-ille变换后的二维“时间-频率”平面进行Radon变换;③对Radon变换结果进行积分然后可以估计走动斜率.

图4 基于Wigner-Radon变换的多普勒调频率估计示意图

3 仿 真

仿真中系统参数：信号带宽100 MHz,脉冲重复频率200 Hz,脉冲宽度10 μ s,载机速度100 m/s;载机高度6 km,正侧视距离Rg=30 km,接收斜视角.仿真中地面点目标相对位置关系如图6所示,每组目标的距离向间隔为5 m;每组目标的方位间隔为1.75 m.

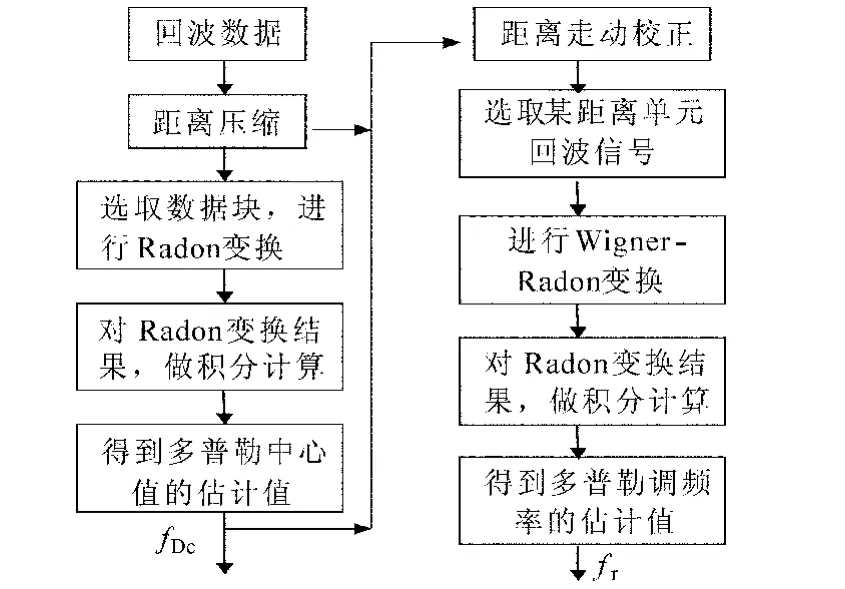
图5 多普勒参数估计流程

图6 仿真点目标位置关系

图7给出了基于Radon变换的多普勒中心估计结果,其中图a)为回波数据距离压缩后的结果;图b)为对距离压缩后的二维平面进行Radon变换的结果;图c)为对Radon变换结果沿距离向积分的结果,其中n表示积分运算中的指数变量.图8给出了基于Radon变换的多普勒调频率估计结果和最终成像结果,其中图a)对某距离单元回波进行Wigner-Radon变换后,沿时间维积分的结果.对本文的仿真模型,基于Radon变换的多普勒参数估计方法,得到的估计值为：多普勒中心 fDc=221.74 Hz,多普勒调频率基于以上估计得到的多普勒参数,得到了如图8 b)的最终成像结果.

该方法中,主要计算量集中在 Radon变换上,在实际应用中,为了兼顾多普勒参数估计准确度和时间效率,在进行多普勒中心估计时,可以根据距离压缩后的图像数据选取m×n大小的数据块进行Radon变换,这样在实际数据的处理中,可以沿方位向实时选取成像数据块,得到实时的多普勒中心估计结果,图7b)、c)就是选取数据块大小为250×1 000时的仿真结果;在进行多普勒调频率估计时,沿方位向实时选取某距离单元的回波数据块,获得实时多普勒调频率的估计,图8a)就是选取某距离单元沿方位向1 000个采样点的仿真结果.

图7 基于Radon变换的多普勒中心估计

图8 基于Radon变换的多普勒调频率估计结果和最终成像结果

4 结束语

多普勒参数估计是SAR精确成像处理的重要组成部分.对多普勒中心频率进行估计,通常用的是谱域相关估计法,包括多普勒频谱分析法、能量均衡法、时域相关法等.这些方法都是用回波信号的方位谱来估计多普勒中心频率,当成像景物为均匀背景时,它们将得到好的结果,当成像景物有只通过部分波束的强散射点,它将造成平均功率谱的扭曲,进而影响多普勒中心频率的估计,而且存在多普勒模糊的问题.本文提出了利用Radon变换实现SAR多普勒参数估计的方法,通过选择适当的数据窗口大小,该方法能够准确、实时地基于回波数据估计出多普勒中心和多普勒调频率,而且不存在多普勒模糊的问题,它是一种可行的基于回波数据的SAR多普勒参数估计方法.

[1]Madsen S D.Estimating the doppler centroid of SAR data[J].IEEE Trans.On AES,1989,25(2)：134-140.

[2]Moreira J R.A new method of aircraft motion error extraction from radar raw radar data for real time motion compensation[J].IEEE Transactions on Geoscience and Remote Sensing,1990,28(4)：620-626.

[3]Thomas M,Alberto M.An algorithm correction using the phase information in SAR raw data for airborne motion error[C]//Proceedings of EUSAR＇96, 1996：139-142.

[4]刘永坦.雷达成像技术[M].哈尔滨：哈尔滨工业大学出版社,1999.

[5] Kong Y K,Cho B L,Kim Y S.Ambiguity-free Doppler centroid estimation technique for airborne SAR using the Radon Transform[J].IEEE Trans. Geosci.Remote Sensing,2005,43：716-721.

[6]Amaya M O,Loffeld O,Stefan K.Comparison of doppler centroid estimators in bistatic airborne SAR [C]//Proceedings of IGASS,Seoul,Korea：2005, 3：1963-1966.

[7]汤子跃,朱敏惠.一种SAR图像舰船属迹的CFAR检测方法[J].电子学报,2002,30(9)：1336-1339.

[8]石 敏,张静远,蒋兴舟.基于匹配追踪和Radon变换的LFM信号宽带时延-时间伸缩声成像方法[J].武汉理工大学学报：交通科学与工程版,2006, 38(3)：381-383.