基于新型性能指标的冗余度机械臂重复运动规划之方案分析与验证＊

张雨浓 郭东生 蔡炳煌 易称福

(中山大学信息科学与技术学院 广州 510006)

作为20世纪人类科学技术进步的重大成果之一,机器人在现实中有着重要的意义,如它们可以在危险或者恶劣的环境(如超高温、超低温)下工作、搬运放射性物质和重物、以及去探索一些未知的场所[1-2];它们已广泛应用于焊接、喷漆以及装配等实际工程中[3].冗余度机械臂是指末端执行器在执行给定的任务时比其所需的自由度有更多的自由度的机械臂,其能更灵活地执行任务;如PUMA560在仅考虑其末端执行器于笛卡尔空间的位置而不考虑其方向时,其冗余度为3.运动学正解和逆解是冗余度机器人的运动学研究过程的核心内容之一[4-10].本文探讨与分析了一种基于新型性能指标的二次型优化模型以解决关节角偏差问题.原理分析和计算机仿真结果验证了所提出的运动规划方案可有效地消除关节角偏差现象,从而达到关节重复运动的目的.

有道是，“宝贝放错了地方就是垃圾”。依我看，“能量”一旦用错了地方，就是“废品”，甚至是“危险品”。我们知道，毒品中毒有“急性”与“慢性”之分，而慢性中毒更为常见。所谓慢性中毒，是指人体脏器通过吸收毒品，积少成多，慢慢累积，以致形成侵蚀和损伤，且中毒所造成的疾病状态会一直伴随。现实生活中，一些人因为不了解慢性中毒的概念和危害，麻痹大意，吸毒中毒。铁的事实表明，毒品既毒害着身体，也毒害着家庭，更毒害着社会。而像吴业平这样的干部，因为“能量”用错了地方，其造成的危害，并不亚于“毒品”。

1 问题描述

末端执行器的位置和方向向量r(t)与关节向量θ(t)的关系可以用下式表示(为了表述方便,时间参数t从此后略写).

小夏的口吻中不再有之前对她的信赖和感激，反而透着居高临下的怜悯：“他在水吧等你时被围住了，却也不敢走。”她冷冷地瞅她一眼，“他怕你突然来了。”雷染君扔下书包，转身往外跑去。“6楼，38病房。”身后的小夏大声喊道。

霍铁走过去，轻轻揭开遮盖物，仔细观察了一会儿。接着，他把江平叫到了存放蜡料的立柜前，问道：“小江哥哥，你觉得这里有什么变化？”

式中：J(θ)：=∂f(θ)/∂θ∈Rm×n为相关的雅可比矩阵.对于冗余度机械臂来说,m＜n,因此,式(1)和式(2)就有可能存在多个解或无穷多个解.

对于式(2)的求解,传统上一般是采用伪逆的方法.然而,传统的伪逆方法有时可能无法使机械臂实现重复运动,也即闭合的末端执行器轨迹得不到闭合的关节轨迹.当然也能够通过自运动(即,末端执行器不动,控制关节从一种构型到达所期望的构型)来调节关节构型,以回到初始状态,从而达到重复运动的目的,但是这种解决方法的效率不高.最近的研究表明,为了使关节能够重复运动,可以通过最小化关节当前位置与初始位置之间的位移量来减小乃至于消除关节角偏差现象.为此,本文探讨如下的优化性能指标

地方党政领导的用地管地理念发生了较大变化，更多的地方将眼光由新增建设用地转向存量土地挖潜，更多的企业受土地低效闲置处置政策和持有成本的倒逼，提高了主动推进土地开发利用的自觉性和紧迫性。

单爷说的书、编的书太多了，自然有高下之分，这在同行中也是争议不断。但他有一点很了不起，即敢于否定和改动自己的作品。很多名家把一部书说火了，就当代表作立住了，不能动了，以此为范本传下去。而他一部书火了但说得不满意，没事，咱推倒重来，再编一个，仿佛没有心理负担。同样的故事能够有不同的理解，说出不同的变化，这是他无处不在的创新意识。

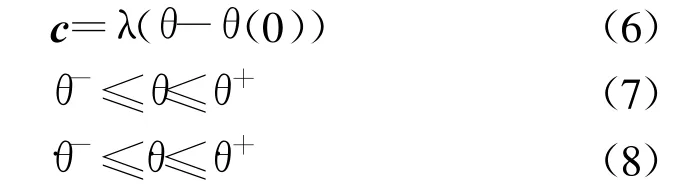
整理式(13)可得

进一步将关节角度约束和关节速度约束合并即可得到双端约束：ξ-≤﹒θ≤ξ+,其中,ξ-和ξ+的第i个元素可分别定义如下.

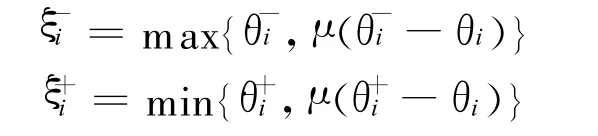
3.1.1 圆形运动轨迹仿真实例 首先,让PUMA560的末端执行器作一个闭合的圆形轨迹,其半径为0.1 m,观察其关节轨迹能否闭合(即,关节角变量能否回到初始状态).令末端执行器的运动周期为10 s,重复运动设计参数λ(见式(6))设为4,关节变量的初始状态为θ(0)=[0,0,0,0,0, 0]T弧度.对此进行计算机模拟仿真,结果如图1、2所示.

图1所示为PUMA560末端执行器在空间中做闭合圆形轨迹运动.可以看出,关节的最终状态和初始状态是重合的,达到了预期的目的.值得指出的是,其最大位置误差不大于4×10-7m.另外,图2给出了机器手臂的关节瞬时变量θ(t)的轨迹图.显然,关节变量都回到了各自的初始状态.因此,二次型优化方案(9)～(11)可认为是一个有效的重复运动优化方案.

2 原理分析

首先,定义一个基于范数的标量对数取值的误差函数

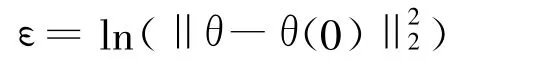
由于函数φ(x)=ln(x)为(0,∞)上的单调递增函数,显然,当二范数‖θ-θ(0)‖取得最小值(即θ=θ(0),表示关节变量在关节空间中的轨迹闭合.但在工程实际中,末态变量与初始变量总是存在一定的误差,如10-5)时,该误差函数ε便可取得最小值.

胡马强把手朝下按了按，颇有领导的派头，示意何泽不说了。然后把头转向一旁的李站长，说老李你是林木专家，做个中间人，说个价格？！李站长模棱两可地说，黄金有价玉无价啊，呵呵呵……

其次,基于负梯度或梯度下降的思想,可以设计得到如下表达式.

(5)当数据到达入口隧道路由器ITR后，对其实行解封装，并将解封装后的数据发至主机X。至此，端到端的交互过程全部完成。

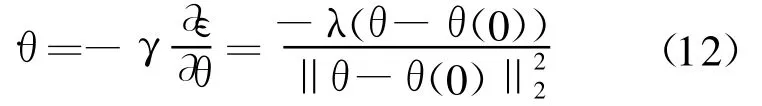
式中：设常数γ=λ/2＞0.该设计思想的目的在于迫使误差函数ε沿负梯度下降方向迅速收敛到其最小值,使得θ(t)趋近于θ(0),从而达到减少或消除关节角偏差现象的目的.由于为一标量,故式(12)也可改写为

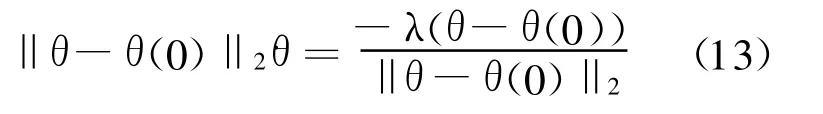
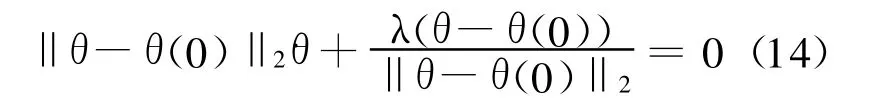
值得指出的是,式(14)只是理想情况,实际问题中还需要考虑很多的因素,如关节物理极限、障碍物躲避以及奇异点等.所以,更为合理的重复运动判据应为最小化

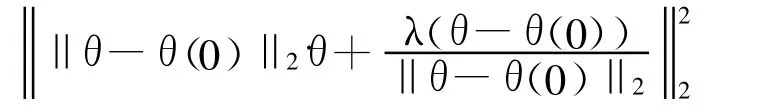
最后,令c=λ(θ-θ(0)),则上述判据也可表示成如下带1/2系数的性能指标

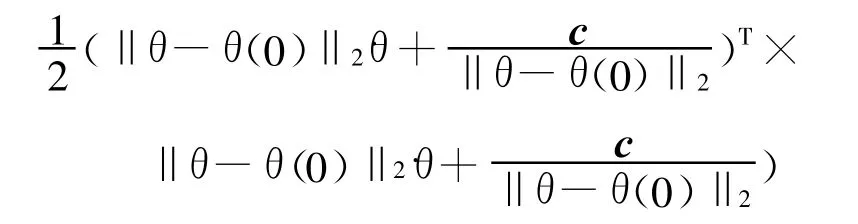
值得指出的是,由于文章是探讨在速度层上解决关节角偏差问题,故可以忽略θ项.则上述带1/2系数的性能指标经过化简之后,便可得到式(3)所示的性能指标,即

最佳适应算法BF(Best Fit):在装入货品时装入到最合适这个货品的箱子里，这个箱子不是第一个可装的箱子，而是最合适的。当没有适合该物体的箱子时，打开一个空箱子。

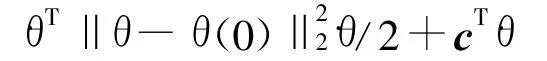
3 计算机仿真

3.1 PUMA560机器手臂

PUMA560可以是功能上冗余的机器手臂,共有6个自由度.若仅考虑其末端执行器在笛卡尔空间的位置而不考虑其取向时,其冗余度则为3.在此将对PUMA560的末端执行器作两个仿真实例,也即,分别做闭合圆形和直线轨迹运动.

式中：常数 μ＞0是用来调节由关节速度决定的可行域.因此,带有物理约束的机械臂的无偏差冗余度解析问题(4)～(8)最终可以描述为如下新的二次型规划问题.

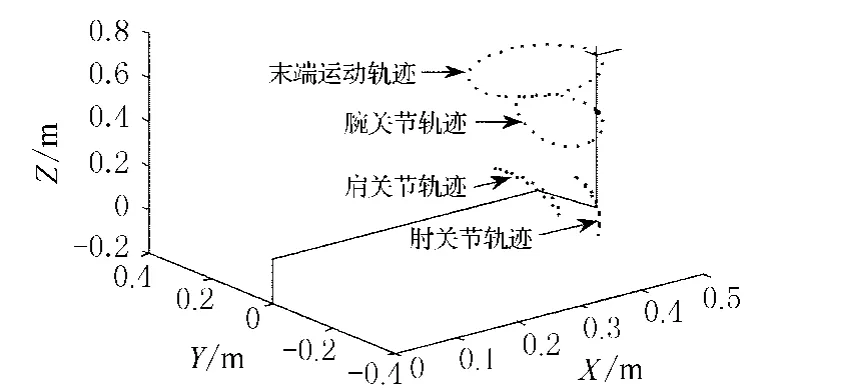
图1 PUMA560机械臂做圆形运动的封闭轨迹

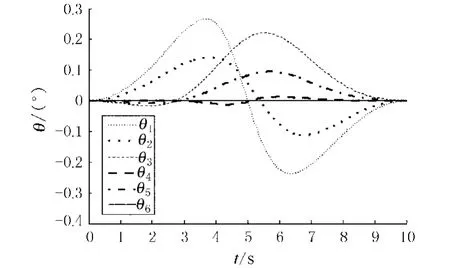
图2 PUM A560机械臂的关节瞬态变量

3.1.2 直线运动轨迹仿真实例 为了全面验证二次型优化方案(9)～(11)的有效性,再次让PUMA560末端执行器作来回直线运动,其(直线)长度为1.125 m,观察其关节轨迹能否重合.末端执行器的运动周期为20 s,重复运动设计参数λ设定为4,关节变量的初始状态为：θ(0)=[0,0,0, 0,0,0]T弧度.对PUMA560机器手臂进行计算机模拟仿真,结果如图3、4所示.

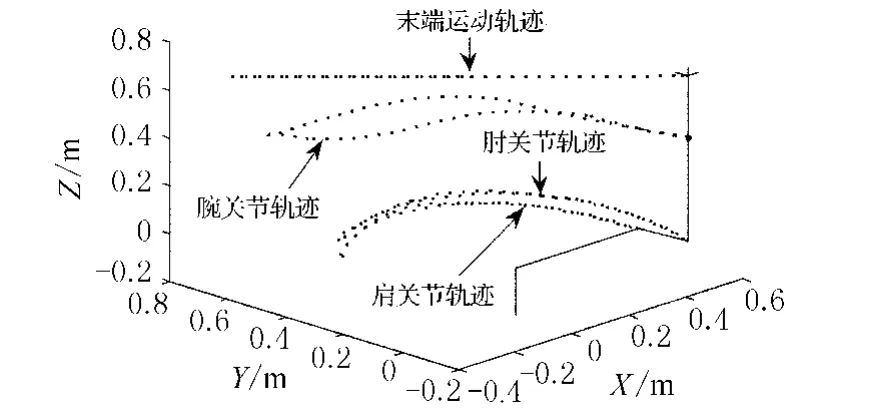
图3 PUMA560机械臂做直线运动的封闭轨迹

从图3可以看出,当末端执行器作完直线运动后,其关节的最终状态与初始状态是重合的,因此也达到了预期目的,且其最大位置误差不大于3×10-6m.另外,从图4给出的关节变量的变化也可以看出,各关节末态与初态也是重合的,即各关节变量都回到了初始状态.可见,二次型优化方案(9)～(11)可以较好地消除关节角偏差现象.

PUMA560机器手臂做圆形和直线运动轨迹的计算机模拟仿真结果表明,基于新型性能指标的二次型优化方案(9)～(11)可以达到重复运动的目的.

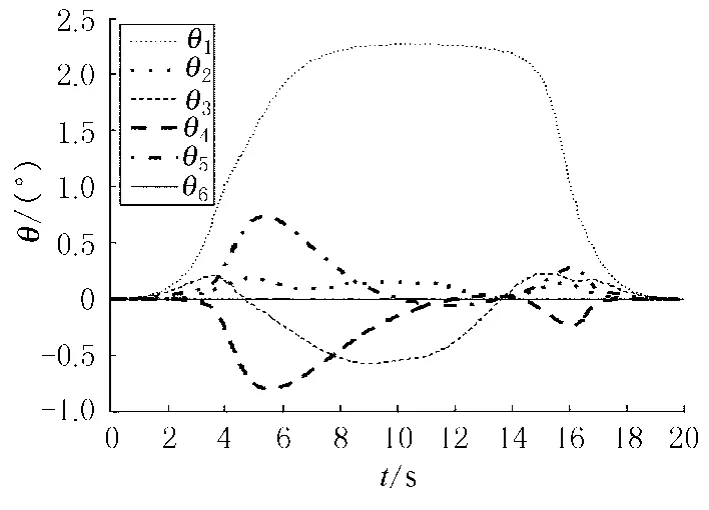
图4 PUM A560机械臂的关节瞬态变量

3.2 四连杆机器手臂

令平面四连杆机器手臂的末端执行器作直线运动轨迹(如图5所示的运动情况),关节的初始状态设为θ(0)=[3π/4,-π/2,-π/4,0]T弧度,观察各关节轨迹能否重合(即,各关节角变量在周期运动后能否回到初始状态),仿真结果如图5、6所示.

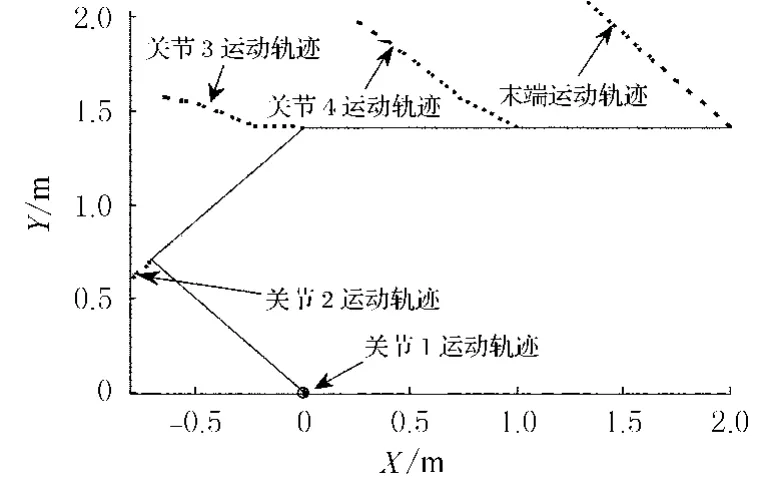
图5 四连杆机械臂做直线运动的封闭轨迹

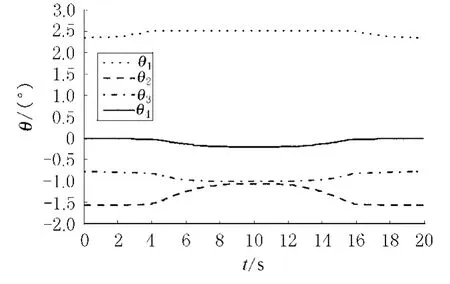
图6 四连杆机械臂的关节瞬态变量

从图5可以看出,四连杆机器手臂的各个关节在完成直线轨迹的运动后,都回到了其初始位置(即,最终状态与初始状态重合);仿真结果达到预期的目的,且其最大位置误差不大于1.4× 10-5m.从图6也可以看出,在经过周期运动之后,平面四连杆机器手臂的各自关节状态都回到初始状态.因此,新方案(9)～(11)可认为是一个有效的关节重复运动冗余度解析方案.

值得指出的是,也对PA10机器手臂作了相关的模拟仿真,即,在空间上做闭合圆形和直线轨迹运动.仿真结果也验证了新方案(9)～(11)可以使各关节均实现重复运动(因篇幅所限,没有给出相关的仿真结果：运动轨迹和关节瞬时变量).

都说现在社会竞争激烈，甚至有人鼓吹生命的诞生就是一场竞争，不能让孩子输在起跑线上。女儿的竞争意识差一点，但我从来没有觉得这是困扰我的难题，在我看来，这个年龄阶段的孩子，他们的任务不是向外延展寻找自己的竞争对手，而应向内积累学会接纳自己。低龄阶段的儿童如果不能接纳他人，其实本质上是不具备接纳自己的能力。

从3种机器手臂(即,PUMA560机械臂、四连杆机械臂和PA10机械臂)的计算机模拟仿真结果可以看出,基于性能指标(9)的二次型优化方案(9)～(11)可以较好地解决关节角偏差问题(现象),以实现机器手臂的关节重复运动,从而可以有效地应用于实际工程当中.

4 结束语

通过定义一个基于范数标量对数取值的误差函数推导出一个新的性能指标,将冗余度机械臂(如PUMA560机械臂和四连杆机械臂)的解析问题最终转化为统一的二次型优化方案(9)～(11).通过对PUMA560机械臂、四连杆机械臂和PA10机械臂进行计算机模拟仿真,验证结果表明该优化方案(9)～(11)能有效地减小或消除关节角偏差现象,在实际工程中可能具有较大的应用价值.

[1]Zhang Y N.Analysis and design of recurrent neural networks and their applications to control and robotic systems[D].Hong Kong：Chinese Univ.,2002.

[2]刘正士,王 勇,陈恩伟.一种水下机器人用多轴力传感器的结构设计[J].中国机械工程,2007,18 (20)：2 481-2 485.

[3]李 艳,王 勇,陈正洪.平面二自由度冗余驱动并联机器人控制实验研究[J].武汉理工大学学报：交通科学与工程版,2009,33(4)：623-626.

[4]刘玉斌,赵 杰,杨永刚.一种新型6-PRRS并联机器人正解研究[J].机械设计与制造,2007(6)：145-146.

[5]刘彩虹,胡吉全,齐晓宁.基于混合遗传算法的连续空间下机器人的路径规划[J].武汉理工大学学报：交通科学与工程版,2003,27(6)：819-821.

[6]张雨浓,符 刚,尹江平.基于双判据优化方法的机器人逆运动学求解[J].大连海事大学学报,2007, 33(3)：1-5.

[7]Klein C A,Huang C H.Review of pseudoinverse control for use with kinematically redundant manipulators[J].IEEE T ransactions on Systems,Man,and Cybernetics,Part B,1983,13：245-250.

[8]Zhang Y N,Ge S S,Lee T H.A unified quadratic programming based on dynamical system approach to joint torque optimization of physically constrained redundant manipulators[J].IEEE T ransactions on Systems,M an,and Cybernetics,Part B,2004,34 (5)：2 126-2 132.

[9]Zhang Y N,Lv X J,Li Z H.Repetitive motion planning of PA10 robot arm subject to joint physical limits and using LVI-based primal-dual neural network [J].Mechatronics,2008,18(9)：475-485.

[10]张雨浓,吕宣姣,杨 智.基于原对偶神经网络的PUMA560机器手臂重复运动规划[J].大连大学学报,2008,29(3)：32-36.