钢连梁剪切屈服型混合连肢墙体系节点滞回性能有限元分析

王 丽,苏明周,徐 明,宋安良

(西安建筑科技大学土木工程学院,陕西西安710055)

1 概 述

现代高层建筑中,连肢墙体系的诞生改善了剪力墙在震后破坏集中在其底部,难以修复、加固等状况,但是在高烈度地震地区,为了提高钢筋混凝土连续梁的抗震性能,其设计和施工难度相应增加。为了缓解这一问题,研究人员采用型钢连梁代替钢筋混凝土连梁,形成混合连肢墙结构。该结构可将钢连梁的两端与埋入剪力墙中的型钢边缘构件进行连接,形成一种新的节点形式,即型钢边缘构件-钢连梁焊接型节点。已有的研究表明,在保证节点域强度的情况下,钢连梁剪切屈服型连接表现出更优良的耗能特性,不但滞回曲线更加饱满稳定,而且刚度和强度无明显退化,是一种具有广阔前景的连接构造形式,值得深入研究和推广[1-6]。

混合结构中钢与混凝土之间存在相互作用,其构造措施复杂,同时节点是连接结构构件与内力传递的关键部位,处于压弯剪的复合应力状态,这对节点的设计提出了较高要求[7-8]。为了研究这种新型结构体系节点的滞回性能,本文采用有限元软件ABAQUS建立钢连梁剪切屈服型混合连肢墙节点的非线性有限元模型,模拟其受力性能及破坏过程,并对钢连梁在循环荷载作用下的滞回性能、核心区应力分布进行了分析,最后提出对设计和应用这种新型连接形式具有重要意义的结论。

2 base有限元模型建立

2.1 研究对象

本文的研究对象由实际结构某中间层上下反弯点之间的剪力墙墙体与半跨钢连梁组成,并按1∶1足尺比例进行设计,有限元模型如图1所示。其中剪力墙高 2 700 mm,宽 1 700 mm,墙厚 250 mm,混凝土采用C35,在剪力墙边缘400 mm范围内设置暗柱,内包焊接H形钢柱,并设4根直径为16 mm的HRB335级纵向钢筋,水平箍筋为 Φ 10@150,节点区域采用Φ 10@90进行加密,为节点提供足够的约束。钢梁伸入剪力墙后焊接在型钢翼缘上,在钢梁与钢柱交接处焊水平钢板加劲肋。构件的截面尺寸和配筋见表1。

图1 base节点有限元模型

表1 构件的截面尺寸和配筋

2.2 有限元模型建立

有限元模型中,型钢和混凝土均采用八结点线性六面体减缩单元(C3D8R),钢筋采用两结点线性三维桁架单元(T3D2)。由于节点核心区柱翼缘及上下加劲肋对中间混凝土形成很好的约束作用,剪力墙中不考虑型钢及钢筋和混凝土之间粘结滑移的影响,认为它们共同工作[9-10],因此,钢筋、型钢边缘构件及伸入墙体部分的钢连梁段均按照实际的空间关系采用内置区域(Embed Region)直接嵌入到混凝土中。

2.3 边界条件及荷载施加

加载方案是剪力墙保持垂直,为了防止在集中荷载作用下,加载处及墙体约束处的混凝土局部破碎,在墙体的底部和顶部均设置刚性垫梁,将底部垫梁的六个方向位移全部约束,用来模拟固接状态,顶部垫梁仅约束 x方向的线位移。荷载分为两步施加,第一步在剪力墙顶部施加恒定竖向均布荷载,当达到预定的轴压系数0.1时,保持荷载值不变;第二步进行低周反复循环加载,在参考点RP-1的U2位移分量上施加竖向荷载,采用位移控制。边界条件及加载情况如图1(b)所示。

2.4 材料的本构模型

2.4.1 钢材的本构模型

分析中钢材采用双线性各向同性强化模型,其牌号为Q235,泊松比取0.3,弹性阶段弹性模量E=2.1×105MPa,塑性阶段取切线模量E0=0.1E。采用Mises屈服准则和相关的流动法则。

2.4.2 混凝土的本构模型

本文采用ABAQUS提供的塑性损伤本构模型来模拟混凝土[11]。该模型引入损伤变量dt和dc衡量由于混凝土损伤而引起的刚度退化;模型还定义了“有效”拉伸和“有效”压缩应力,并以此来确定屈服面或破坏面的大小,其表达式分别为:

式中:损伤因子dt和dc的取值范围从0至1,当值为0时表示材料没有损伤,值为1时表示材料完全破坏;E0为材料的初始弹性(无损)模量;εtpl和εcpl分别为拉伸和压缩等效塑性应变。

混凝土采用《混凝土结构设计规范》(GB50010-2002)推荐的应力-应变关系曲线[12],其受压曲线方程如下:

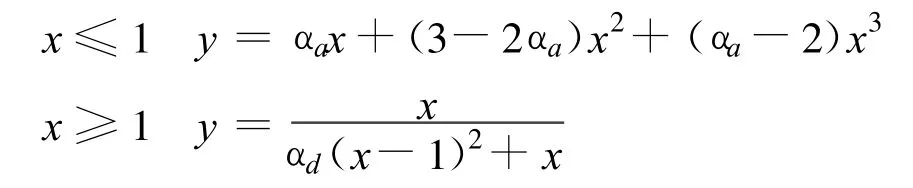
式中:无量纲应力 y=σ/fc,无量纲应变x=ε/εc0,其中fc和εc0分别为混凝土轴心抗压强度和对应的峰值应变。受拉曲线方程为:

式中:无量纲应力y=σ/ft,无量纲应变 x=ε/εt0,其中ft和εt0分别为混凝土轴心抗拉强度和对应的峰值应变。模型中各参数的确定参照文献[13]。

3 节点力学性能分析

3.1 节点的滞回性能分析

结构在低周反复荷载作用下的滞回曲线能够全面的反映结构在地震作用下的各种性能,包括强度、刚度退化性能以及变形、能量吸收能力等,是分析结构或构件地震反应的重要依据。一般认为,滞回曲线越饱满,结构的耗能能力越强,抗震性能越好。图2为base节点模型在循环荷载作用下的荷载-位移(P-Δ)曲线,其中P、Δ分别为梁端竖向荷载和竖向位移。

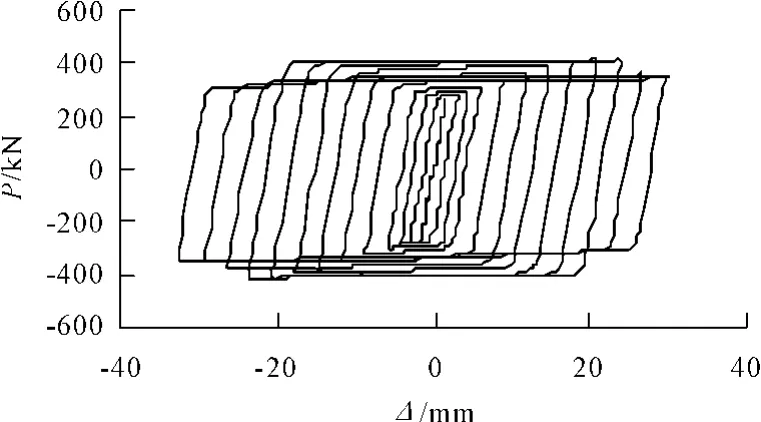
图2 滞回曲线

通过滞回曲线可以看出,在荷载较小时,滞回曲线包围的面积很小,力和位移呈线性关系,卸载后变形恢复到初始位置,试件处于弹性工作阶段;随着荷载的增加,滞回曲线偏离直线,进入弹塑性阶段,此时,滞回环包围的面积逐渐增大,但模型刚度有所下降;本文研究的节点形式承载力稳定性好,具有良好的塑性变形能力和能量耗散特性。

3.2 承载力及延性影响因素分析

为了补充分析钢连梁剪切屈服型混合连肢墙体系节点承载力及延性影响因素,本文将进一步考察轴压比和腹板高厚比的影响。

3.2.1 轴压比的影响

为研究轴压比对钢连梁剪切屈服型混合连肢墙体系节点受力性能的影响,取base节点模型为研究对象,在其剪力墙顶部分别施加相当于0.2、0.3、0.4和0.5倍轴压比的分布荷载。计算得到各工况下的剪力墙主压应力云图如图3所示。从图3中可以看出,轴压比分别为0.2、0.3、0.4和 0.5时,对应的节点区混凝土最大主压应力分别达到32.32、32.24、32.19MPa和32.07 MPa,而整个墙肢的主压应力值分别为5、8、10 MPa和12 MPa左右。随着轴压比的增大,虽然整肢剪力墙的主压应力有所上升,但核心区混凝土主压应力基本没有变化,甚至有轻微的下降。从上述分析可以得出,轴压比在0.1～0.5之间对核心区受压混凝土主压应力影响不大,所以在高轴压比情况下,采用钢连梁剪切屈服型的节点形式具有实用意义。

3.2.2 腹板高厚比的影响

为了研究腹板高厚比对节点性能的影响,采用BH1、BH2、base及BH4四个节点模型进行计算 ,对应的钢连梁截面尺寸信息见表2。

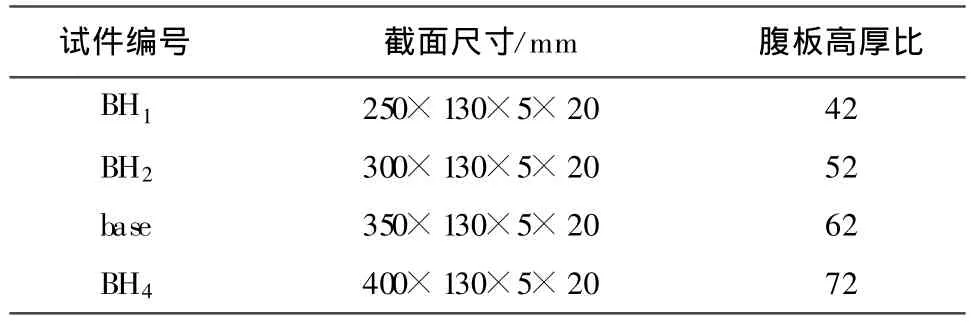
表2 钢连梁截面尺寸

骨架曲线是连接每一级荷载第一次峰值点的连线,能够反映构件在加载过程中的屈服强度、极限强度以及极限变形等。通过计算得到不同高厚比情况下的骨架曲线,如图4所示。从图中可以看出,随着钢连梁腹板高厚比的增大,节点的屈服荷载、极限荷载都有不同程度的提高,其中BH4比BH1的屈服荷载提高了81%,极限荷载提高了64%,但是其骨架曲线的下降段逐渐变陡,表明后期的变形能力逐渐降低,即节点的延性在逐渐变小。

4 结 论

本文应用有限元软件ABAQUS,对钢连梁剪切屈服型混合连肢墙体系节点的受力性能进行计算模拟以及变参分析,主要考虑了轴压比和腹板高厚比两个影响因素对钢连梁及节点核心区受力性能的影响,分析结果表明:

(1)base模型滞回曲线饱满,且刚度下降不大,表明当钢连梁按剪切屈服型设计的节点形式具有良好的耗能性能及延性,适合在高烈度高层建筑结构中使用。

(2)轴压比在0.1～0.5之间对节点核心区受压混凝土主压应力的影响不大,表明钢连梁剪切屈服型的节点形式在高轴压比情况下具有实用意义。

图3 剪力墙主压应力云图(单位:Pa)

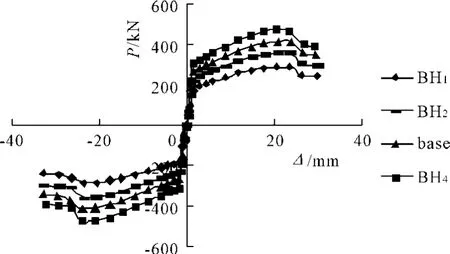
图4 荷载-位移骨架曲线

(3)综合考虑钢连梁腹板高厚比对节点耗能性能及延性的影响规律,钢连梁腹板的高厚比在45～65之间时,性能最优良。

[1]Kent A.Harries,Denis Mitchell,William D.Cook and Richard G.Redwood.Seismic response of steel beams coupling concrete walls[J].Journal of Structural Engineering,1993,119(12):3611-3629.

[2]Kent A.Harries,J.Dan'l Moulton and Robert L.Clemson.parametric study of coupled wall behavior-implications for the design of coupling beams[J].Journal of Structural Engineering,2004,130(3):480-488.

[3]Kent A.Harries,Denis Mitchell,William D.Cook and Richard G.Redwood.Seismic design of coupled walls-A case for mixed construction[J].Canada Journal of Civil Engineering,1997,24:448-459.

[4]Wan-Shin Park,Hyun-Do Yun.Seismic behaviour and design of steel coupling beams in a hybrid coupled shear wall systems[J].Nuclear Engineering and Design,2006,236:2474-2484.

[5]Wan-Shin Park,Hyun-Do Yun,Sun-Kyoung Hwang,et al.Shear strength of the connection between a steel coupling beam and a reinforced concrete shear wall in a hybrid wallsystem[J].Journal of Constructional Steel Research,2005,61:912-941.

[6]Wan-Shin Park,Hyun-Do Yun.The bearing strength of steel coupling beam-reinforced concrete shearwall connections[J].Nuclear Engineering and Design,2006,236:77-93.

[7]郭峰.含型钢边缘构件的混合连肢墙体系钢梁与剪力墙的连接性能[D].西安:西安建筑科技大学,2007:19-20.

[8]苏明周,郭峰.高层建筑混合连肢墙体系的抗震性能[J].建筑钢结构进展,2009,11(1):38-45.

[9]王宏彦,赵鸿铁,薛建阳,等.型钢混凝土偏压柱粘结滑移性能的试验研究[J].西安建筑科技大学学报(自然科学版),2003,35(3):217-220.

[10]薛建阳,杨 勇,赵鸿铁.型钢混凝土构件粘结滑移性能试验及分析[J].工业建筑,2005,35(增):142-146.

[11]王金昌,陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006:83-94.

[12]中华人民共和国建设部.GB50010-2002.混凝土结构设计规范[S].北京:中国建筑工业出版社,2002:206-208.

[13]芦学磊.削弱型钢连梁抗震性能及其对剪力墙的影响[D].哈尔滨:哈尔滨工业大学,2008:54-59.