海堤地基真空-堆载联合预压有限元计算研究

王柏欢,尹志标,陆玉琳

(1.中交上航局航道建设有限公司,浙江宁波315200;2.河海大学,江苏南京210098)

真空预压法及真空-堆载联合预压法在各类工程的软基处理中的实际应用越来越多[1-3],对其计算方法的研究已取得了一定成果。目前常用的计算方法主要有解析法、有限单元法[4]。

由于真空-堆载联合预压处理地基都要打设砂井或塑料排水板(以下简称PVD),从而形成了砂井地基,进行平面应变简化时通常是调整土体的渗透系数,将三维问题转化为平面应变问题,计算模型和实际场地的力学、渗流有较大区别。进行三维分析在理论上是相对较完善的,但是PVD的存在使计算规模比较庞大,因此真空-堆载联合预压处理地基的三维计算未得到推广。本文结合某海堤现场试验,根据海堤地基的变形特点,对真空-堆载联合预压处理的海堤软基的三维简化模型进行了计算,该模型简化条件较少,可以考虑排水板的空间分布特征等因素。结合某海堤地基处理实际工程,进行了计算并与实测数据进行了比较、分析,得到了一些有益的结论。

1 真空-堆载联合预压海堤现场试验

某海堤位于广东省中山市,其中有一长度为420 m的试验段,段内软土较厚,海堤填土高度为10 m,考虑到高填土巨大的侧压力对结构物产生的影响不容忽视,以及与路线斜交的桥台桩基,若处理不当,必将严重影响结构安全,因此经过考虑后采用真空-堆载联合预压法处理。

该段内的土层分布情况如下:①砂垫层:灰白色、褐黄色,主要成分为细 ～中砂,中密,为新近填砂。该层呈层状分布,层厚1.60 m;②耕植土层:土黄色、灰黑色,主要成分为粘土,湿,软～可塑,厚度3.90 m;③淤泥质粘土:灰黑色,黑色,湿～饱和,流～软塑,含腐殖质,有泥臭味;含少量粉细砂及贝壳碎屑,层厚 9.28 m;④淤泥层:灰黑色,黑色,饱和,流～软塑,含腐殖质,有泥臭味;含少量粉细砂,有砂感,层厚4.50 m;⑤粘土层:土黄色,灰黄色,主要成分为粉、粘粒,粘性强,局部含淤泥质,湿,可塑～硬塑,以可塑为主。层厚6.60 m;⑥淤泥质粘土:灰黑色,黑色,可塑,主要成分为粘性土,含腐木、枯叶,有泥臭味;含少量粉细砂,有砂感,层厚4.20 m。

其中第3层、4层的淤泥土质指标较差,呈流塑状,含水率高,强度低,孔隙比大,并富含有机质,因此主要针对该层进行处理。

在预压施工前,按照正方形排列、间距1.3 m打入21 m长的PVD,工程断面如图1所示。真空预压以及堆载施工的加载情况如图2、图3所示。

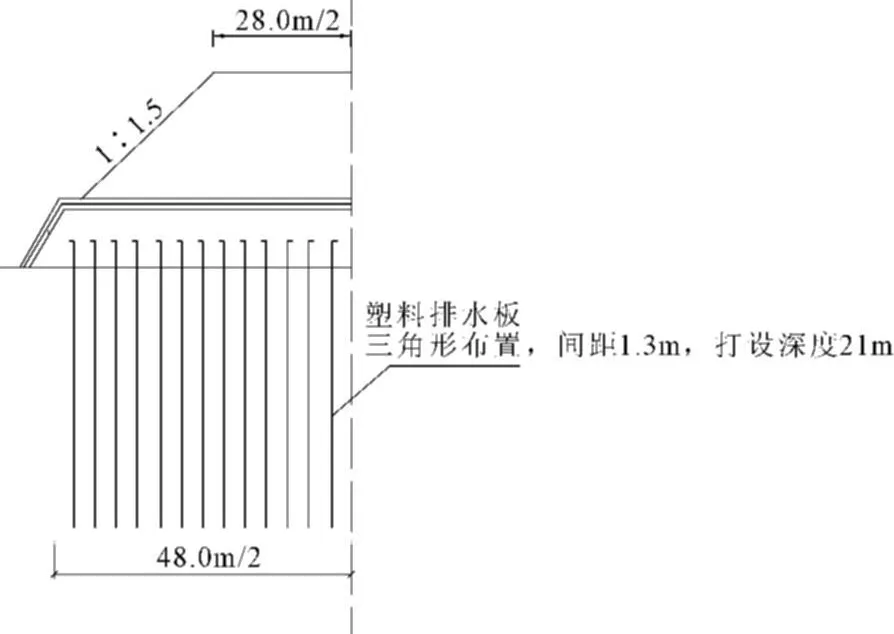
图1 工程断面

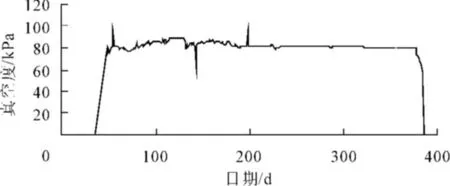
图2 真空荷载曲线

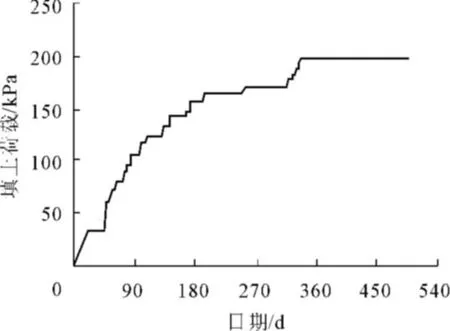
图3 堆载荷载曲线

2 三维有限元计算方法

2.1 真空-堆载联合预压中海堤地基的变形特点

海堤软基都打设了PVD之后,要考虑PVD的作用以及PVD之间土体的变形、孔压变化,可以沿软基长度方向取一段作为分析对象,由于可假定软基沿长度方向的位移为0,因此可将这一小段取出来类似于平面应变问题中的单位厚度,但是在该小段内考虑PVD的布置,如图4所示。这样的简化模型未考虑软基沿长度方向的变形,但是考虑了PVD的作用位置而无需将其简化为砂墙地基,除了在软基的两端,这个简化条件是合适的。

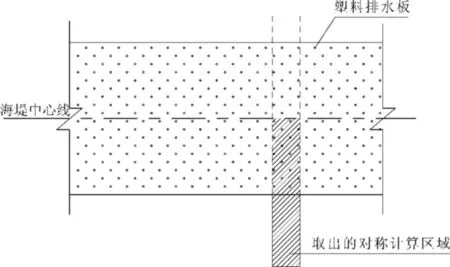
图4 计算模型示意图

计算中采用的土体模型为修正剑桥模型。修正剑桥模型的参数如下:λ为e-lnp′平面上等向压缩曲线的坡度;κ为e-lnp′平面上回弹曲线的坡度;ecs为临界状态线当p′=1时的孔隙比;M为q-p′平面临界状态线的坡度;G,γ为弹性剪切模量和泊松比,可任取一个。修正剑桥模型的具体参数意义在此不再赘述,见参考文献[5]。

结合上述海堤地基的变性特点,用abaqus进行了计算。

2.2 PVD参数的选取

PVD在实际工程设计中已经得到了相当广泛的应用,但是同PVD有关设计时采用的参数仍然存在一定的争议,对计算结果能产生较大的影响,因此,国内外广泛开展了室内试验、现场试验和数值分析,对PVD参数确定进行了深入的研究,但仍未能形成较为统一的认识,本节在前人文献的基础上,结合自己在有限元计算过程中的一些体会,对PVD参数进行总结与探讨。

由Hansbo解可知[6],在设计计算中所需要的参数主要有两方面,一方面是同PVD本身的排水性能以及在打设PVD过程中对周围土体的扰动影响,即涂抹效应;另一方面是土体本身的物理力学性质指标。

在涉及PVD自身特性的参数中,最为重要的是PVD的长期通水能力,其对设计计算结果的影响较大。在PVD使用过程中,PVD的长期通水能力会较使用之前有较大的下降。因此,在设计时,必须采用具备较大通水能力的排水板,并且计算时应采用长期通水能力,在测试PVD通水能力时,必须尽可能的模拟现场实际情况,Hansbo详细总结分析了用于测试PVD长期通水能力的试验方法和仪器。造成PVD长期通水能力下降,通常称为井阻的主要有以下原因:PVD侧向受到固结土压力;PVD堵塞及弯曲。一般可采用qw=100 m3/a或50 m3/a作为设计取值。

在排水板打设过程中,由于打设机械的影响,会对排水板周围土体产生一定的扰动,并在排水板周围形成涂抹区,涂抹区产生的原因主要有二:一是靠近排水板周围土体,由于机械的影响,土体结构完全破坏,导致水平向渗透系数的大幅下降;二是由于排水板打设是一个相对较快的过程,在打设过程中,必然使周围土体中产生较高的超静孔隙水压力,土体中的超静孔隙水压力消散导致土体固结,孔隙比减小,使得涂抹区土体的渗透系数下降。涂抹区的范围主要取决于钻机钻头的尺寸与截面形状。

对于涂抹区的大小以及涂抹区土体渗透系数下降的幅度,国内外开展了广泛深入的研究。由文献[4]可知,土体渗透系数kh与涂抹区渗透系数ks之间的比值变化范围较大,可以在1～15之间,因此在实际计算过程中,如何更好的考虑涂抹区渗透系数变化情况还需要进一步研究,通常情况下可以选取kh/ks=2～8,根据笔者计算的一些体会,建议采用kh/ks=4～6,本研究取值为5。

2.3 计算断面及参数

选取典型断面进行了三维数值计算,计算的工程断面如图1所示。

2.3.1 土体模型参数

根据室内试验资料,可以得到数值计算所需要的修正剑桥模型参数。如表1所示。其中第①层砂垫层的渗透系数较大,不考虑其固结沉降,在计算中视为边界条件。

2.3.2 PVD参数

考虑到PVD对海堤地基在受力方面的作用不大,主要考虑其通水能力,因此定义其计算参数为:弹性模量 E=10 kPa,渗透系数k=2.5×10-3cm/s。

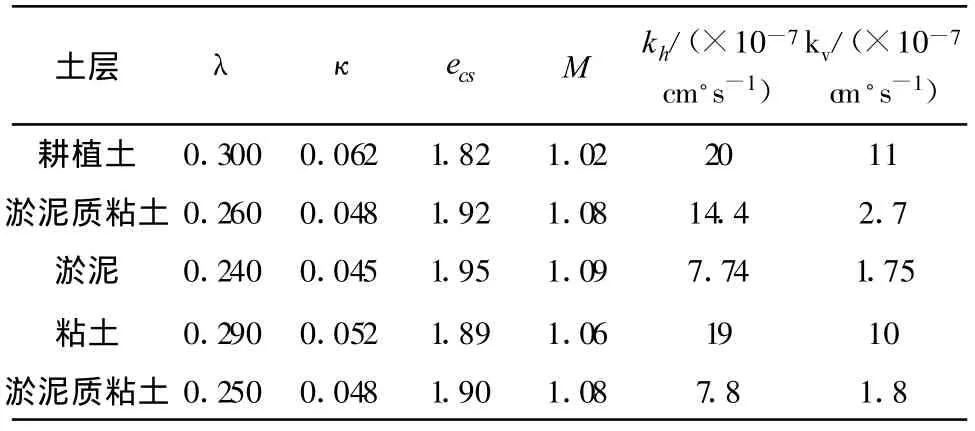
表1 有限元计算所需的剑桥模型参数

2.4 有限元网格及边界条件

2.4.1 有限元计算网格

选取一段加固区进行计算,由该路段的排水板布置间距可得有限元网格的平面示意图以及透视图分别如图5、图6所示。划分的有限元网格中八结点土体单元共计41520个。

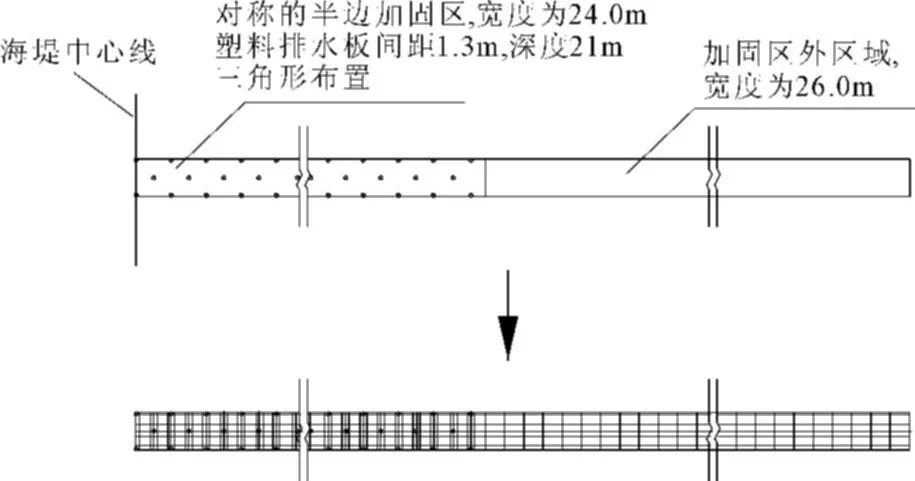
图5 模型的转化

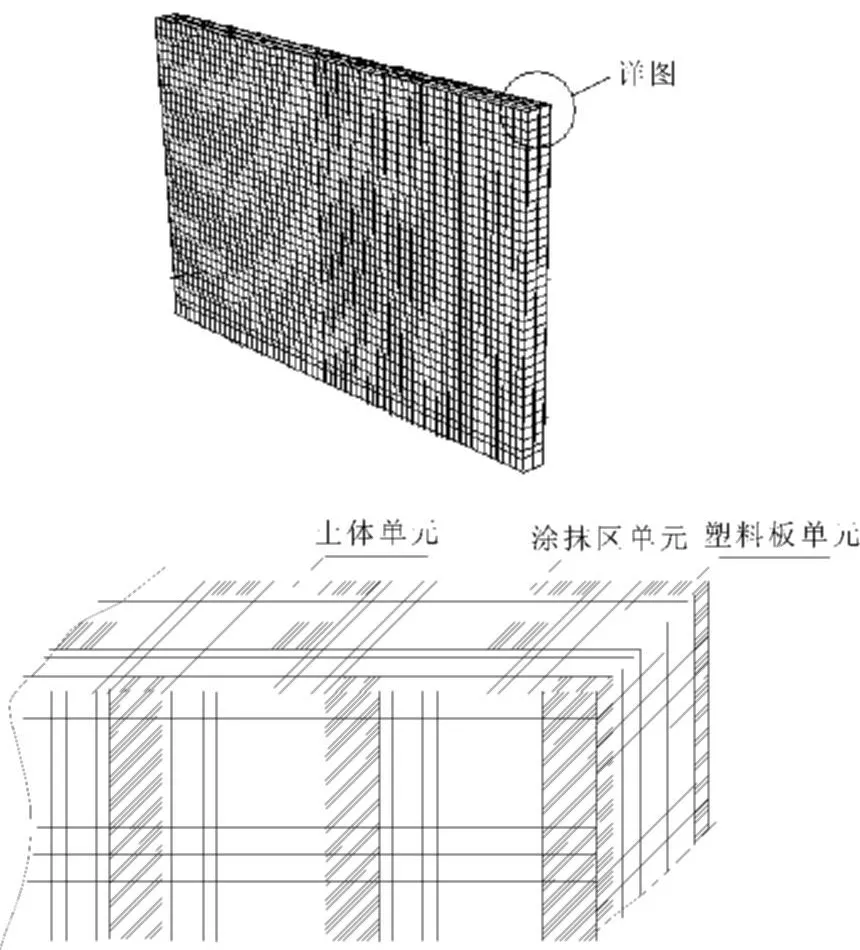
图6 有限元网格

2.4.2 边界约束条件及计算用加载过程

进行有限元分析时,其约束条件为:竖向边界面均为水平位移约束以及不透水边界,竖向位移无约束,基底为竖向、水平向位移约束,同时也是不透水边界。地面处,加固区和非加固区位移自由,非加固区孔压为0。加固区表面孔压为0。真空和堆载的实际加载曲线以及计算用简化加载曲线如图7、图8所示。

孔压边界取为:地基表面孔隙水压力为0,其它边界的孔压未知。真空荷载的施加模拟为地表孔隙水压力减小为-80 kPa。

在堆载时,将填土折算成等效结点荷载按实际加载曲线施加上去。

荷载施加曲线如图7、图8所示。

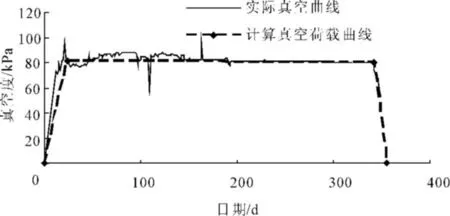
图7 真空荷载加载及计算曲线

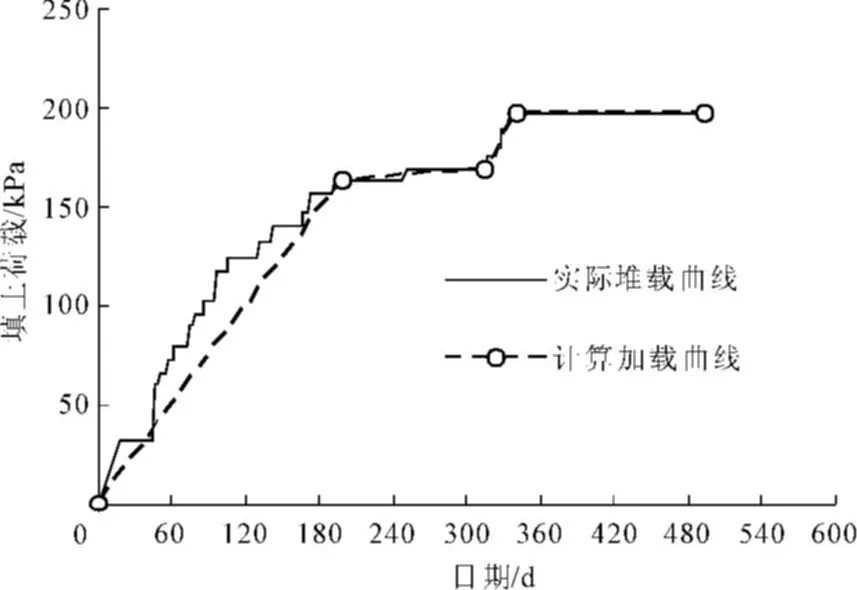
图8 堆载荷载加载及计算曲线

3 计算结果分析

3.1 表面沉降计算结果

计算的加固区中部及右路肩处的表面沉降曲线如图9、图10所示。从图中可以看到,路堤中心处的沉降计算结果与实测值比较接近,路肩处的沉降计算值则稍大于实测值。其原因主要是计算荷载以路堤中心处为标准,其包括了沉降补方的荷载,而路肩处的沉降补方量要少于路堤中心处,计算时为了方便,仅考虑路堤中心处补方量,因此计算结果偏大。

3.2 分层沉降计算结果

本次计算的分层沉降值以及实测值如图11所示。其中实测仪器到施工后200 d左右破坏,因此实测仅有施工200 d以内的数据。计算值在初期要大于实测值,但是随着堆载的施加,两者逐渐接近。从这个角度而言,目前的真空荷载作用下的地基计算方法还需要进一步研究。前述的表面沉降亦有这个现象,即真空预压阶段的计算值大于实测值。不过随着堆载的作用,计算值和实测值逐渐趋于一致。

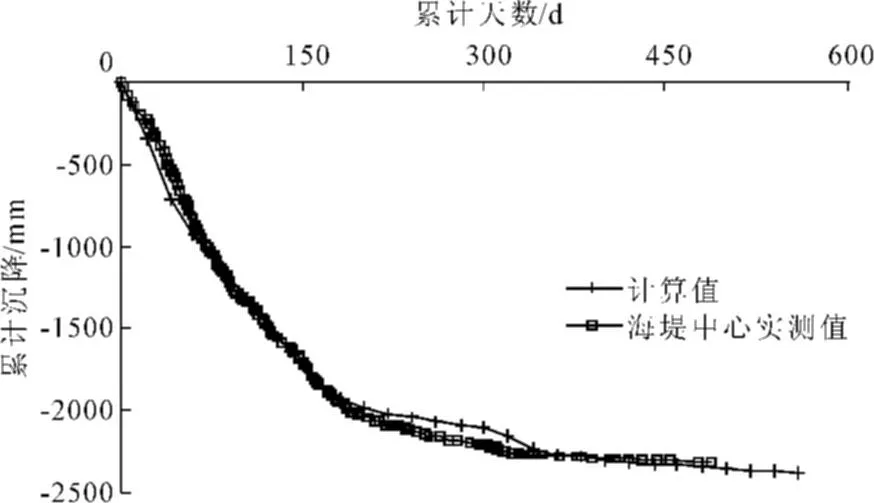
图9 加固区中心表面沉降

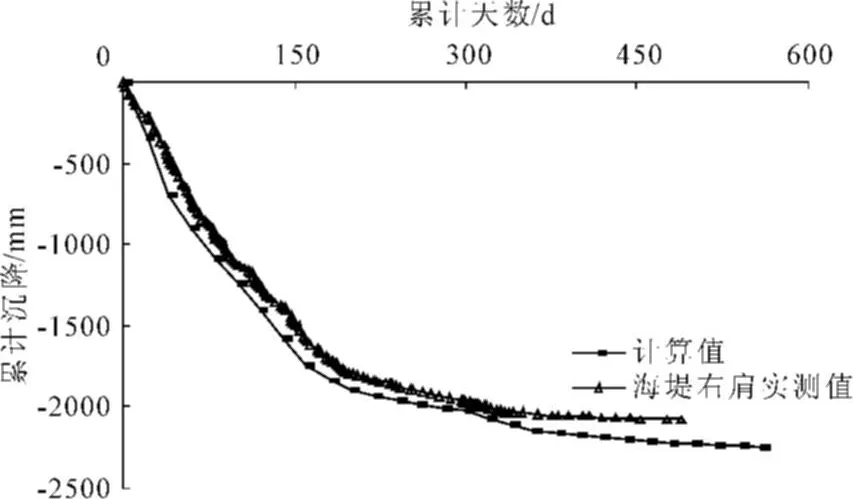
图10 右路肩表面沉降

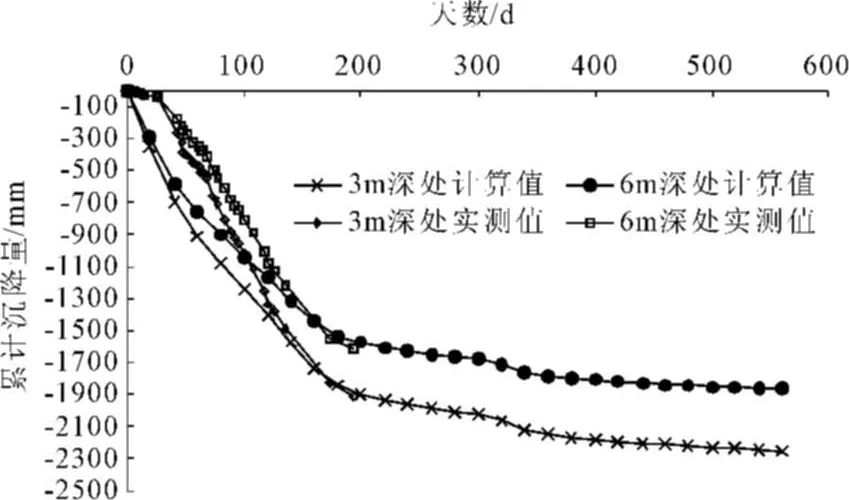
图11 分层沉降计算值

3.3 水平位移计算

图12是1 m深度处的水平位移实测值以及计算值,由于测斜管离加固区有一定距离,因此水平位移幅度不是很大。计算值和实测值的趋势基本一致,即在真空荷载施加之前,由于有砂垫层的作用,加固区外土体是向外位移即挤出的(收缩为负值),真空荷载作用后,土体开始向内收缩,而随着堆载的进一步施加,土体又开始向外挤出。计算值要大于实测值,分析其原因,主要是由于土体在挤出、收缩的过程中会产生裂缝,产生的部分裂缝位于测斜管和加固区之间,目前的计算理论无法模拟、反映裂缝的作用和影响,因此计算值要大于实测值。

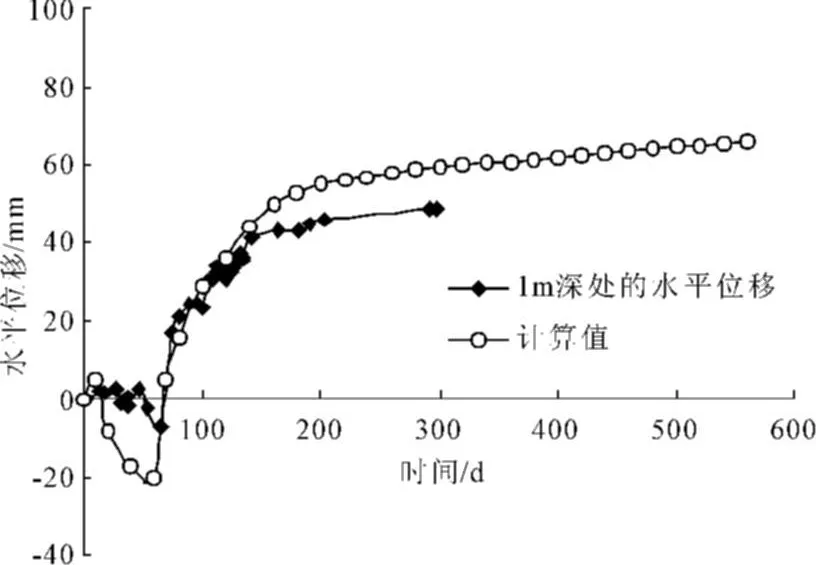
图12 1 m深度的水平位移计算值

3.4 孔隙水压力计算结果

孔隙水压力观测是了解地基土体固结状态比较直接的手段,根据孔隙水压力的变化规律,可分析地基土体的固结机理;通过不同深度孔压随时间变化曲线的实测资料,可进一步研究土体强度增长规律。

图13为5 m深度处的孔压实测值以及计算值。从图中可看出,计算值的变化趋势与加载过程是吻合的,符合孔压升高-消散-加压升高-再消散的规律。实测值也基本遵循了这个规律,两者在数值上还是有一定的差异。

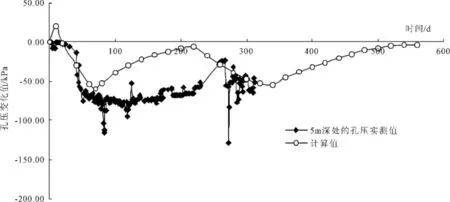
图13 5 m深度处的孔压对比曲线

3.5 有限元计算误差分析

本文的三维计算结果与实测值也有一定的差异,造成这种差别主要有下列一些原因:

本课题数值计算的理论基础是Biot固结方程。Biot固结方程的基本假定之一是土体完全饱和。在本文的实际工程中,地下水位在地面下1 m～2 m,地下水位之上的土体为非饱和状态,因此会造成一定的误差。

此外,在推导Biot固结有限元公式的时候,对孔隙水的流动采用了达西定理描述,然而已有一些文献对该假定提出不同意见,认为孔隙水的流动并不严格遵循达西定理。

由于土体本身的复杂性,有限元分析选取的土体本构模型不能完全反映土体的变形特性。

有限元分析时所采用的加荷方式及加荷级数与真实的加荷情况有一定差异。数值计算的荷载施加是一根比较平滑的曲线,而实际的荷载施加曲线则曲折得多。

计算时未考虑土体渗透系数随时间的变化。此外对PVD的渗透系数,本文计算时取值为上下一致。而考虑到深层土体中的PVD受到较大的水平向应力,因此会导致其通水能力降低,渗透系数的取值也应相应降低。由于缺乏足够的试验数据以及理论研究,本文没有考虑该影响。

计算模型同实际模型有一定差别,边界条件的选取仍需进一步的研究、改进以模拟实际情况。

4 结 语

从上述工程实例分析可以看出,从已有的实测值、计算值比较来看,本文的计算结果同实测值吻合还是较好的。得到的结论如下:

(1)本研究采用了三维Biot固结有限元法,在计算中采用了修正剑桥模型,根据海底地基的变形特点而采用的三维计算模型,与以往的方法相比,可不必考虑转化为平面问题时带来的与实际情况不符的矛盾,较全面地考虑了打设了PVD后的空间效应,计算结果与实测值较为接近。

(2)本研究的孔压计算结果在加固区内与实测结果的趋势基本吻合,而影响区的孔压计算结果还需要进一步试验验证。

(3)对有限元计算的误差原因进行了分析,对今后的相关研究提供了建议和参考。

[1] 张照华.真空联合堆载预压排水固结法在沿海吹填造地中的应用[J].水利与建筑工程学报,2009,7(3):123-126.

[2] 董江平,张雄壮,洪 雷,宋恩润.无砂垫层真空预压法提高吹填淤泥地基承载力试验研究[J].水利与建筑工程学报,2010,8(4):131-133.

[3] 徐猛,黄家青,唐彤芝.软式透水管在高速公路真空预压工程中的应用研究[J].水利与建筑工程学报,2007,5(2):22-26.

[4] 彭吉力.真空-堆载联合预压法加固机理与计算理论研究[D].南京:河海大学,2003.

[5] 黄文熙.土的工程性质(第一版)[M].北京:水利电力出版社,1983.

[6] Arutiunian R N.Vacuum-accelerated stabilization of liquefied soils in landslide body[C]//Proc.ofⅧ ECSMFE,1983,(2):575-576.