层次分析—模糊综合评判联合法在常绿杜鹃花引种气候适宜区位预测中的应用

庄 峤，朱文涛，赵 越，姜程程

(山东大学威海分校数学与统计学院，山东威海 264209)

l 引言

杜鹃花是具有极高的观赏价值的世界名花，但是由于其生长对气候条件的选择相对苛刻，只能在相对较小的特定区域生长。在这种情况下，杜鹃花的引种适应性分析就引起了相关科研工作者的较大关注。

杜鹃花属名贵物种，如果对栽培区位不加选择地进行试栽，经济成本过高。为了减少不必要的引种成本，我们希望通过杜鹃花专家提供的杜鹃花生长—关键气候因子经验参数表，借助数学方法对“华西雨屏带”［l］中的常绿杜鹃花的适宜引种区位进行预测。事实上，在我们前期的工作［2］中，已经用加权欧几里得距离的方法，根据气候适应性的优劣，对备选引种区域进行了排序。但是作为一种方法，加权欧几里得距离法在处理带权指标对所需要评判的目标的影响的问题时，虽然具备一定的合理性，但毕竟方法本身是粗糙的、单一的，而需要解决的问题却是复杂的、系统的，因此即便利用这种方法预测杜鹃花引种气候适宜区位的结果和杜鹃花专家的判断具有一定的一致性，该结果的置信水平还是比较低。

我们需要解决的问题，是根据带权的指标，确定方案层(各个备选城市)对目标层(选择适宜引种区位)的权重。解决这一类问题，层次分析法(AHP，Analytic Hierarchy Process)是一种比较系统而成熟的方法。我们的研究方法正是在AHP的基础上，结合问题实际，作了必要的改进;利用改进了的AHP计算出了备选城市对引种适应度的权重。另一方面，又用模糊综合评判法进行了预测。本文试图通过联合这两种方法，给出一个具有较高置信水平的预测结果。

2 研究方法

2.l 准备工作

2.l.l 基础资料的收集:收集天津、唐山、锦州、营口、大连、潍坊、威海、青岛、日照及沈阳、丹东、长春、哈尔滨、延吉、济南、连云港、东台、上海、杭州、成都、昆明、贵阳等22个典型气候区所在地的气象要素原始数据资料。

2.l.2 确定杜鹃花生长—关键气候因子经验参数表(参见表l)

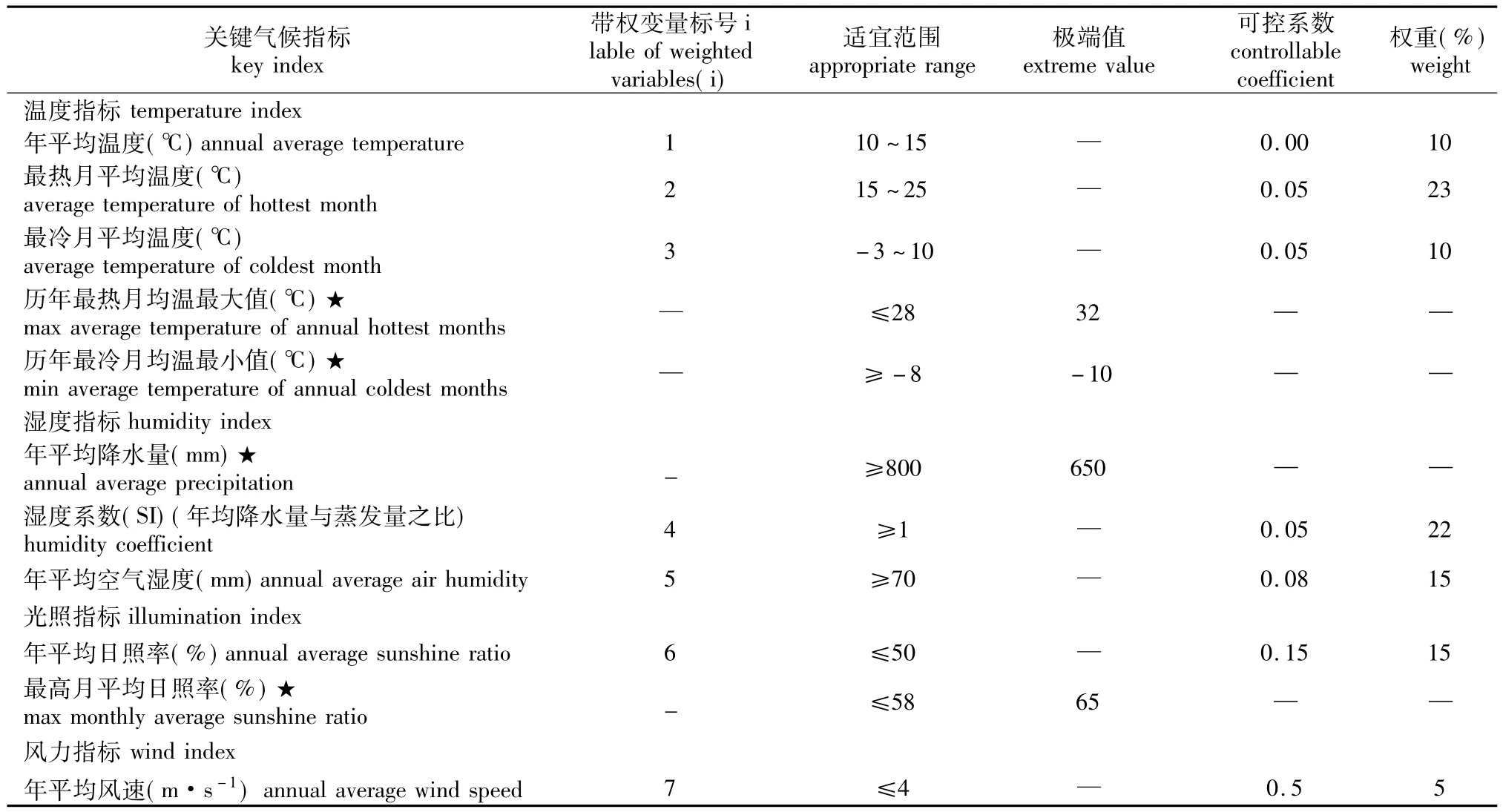
表l 杜鹃花生长—关键气候因子经验参数表Table l Key climatic indexes of cultivation of rhododendron

2.l.2 区域城市气候指标表

(l)根据“门槛指标”的筛选，确定出仅威海、青岛、日照、东台、上海、大连、成都、贵阳入选有效样本集。

(2)有效样本集中包含的区域城市样本指标表(不含“门槛指标”)。区域城市气候指标表参见表2。

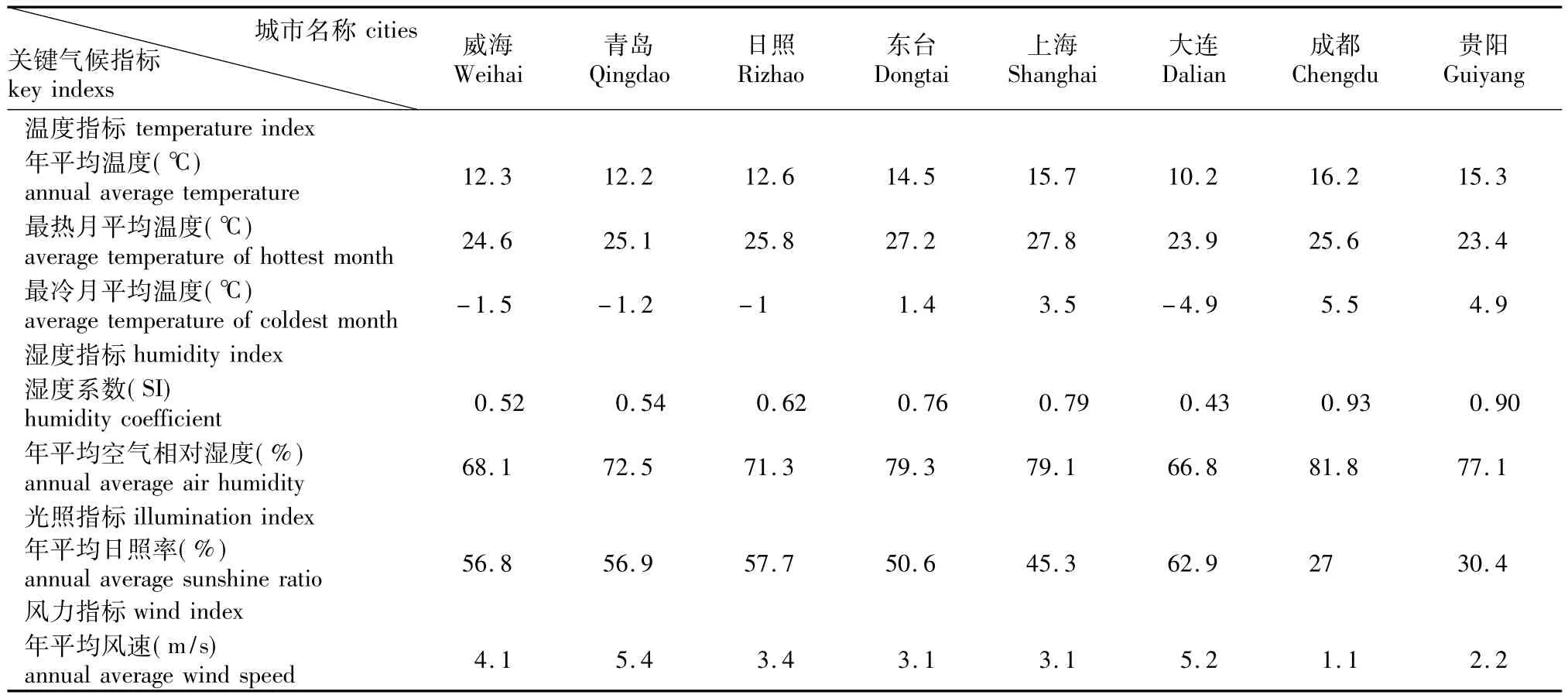
表2 有效样本集中包含的区域城市样本指标表(不含“门槛指标”)Table 2 Key indexes of each city in the valid sample set(not including the extreme indexes)

2.2 层析分析(AHP)预测法

层 次 分 析 法［3，5，6］(The analytic hierarchy process)，简称AHP，在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。它是一种定性和定量相结合的、系统化、层次化的分析方法［3］。由于它在处理复杂的决策问题上的实用性和有效性［5］，很快在世界范围得到重视。它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗和环境等领域。

层次分析法的基本思想与人对一个复杂的决策问题的思维、判断过程大体上是一样的。这种方法把决策问题分为3个层次，由上向下依次是目标层、准则层、方案层。利用这种方法求解复杂决策问题时，首先要根据主观经验(当然这种主观经验是建立在客观事实基础上的)确定准则层对目标层的权重;其次，就每一个准则，确定各个方案对准则层的权重;最后，将方案层对准则层的权重及准则层对目标层的权重进行综合，选出最佳方案。其实，所谓最佳方案，就是指对目标层权值最高的方案。方案层对目标层的权值，针对不同的问题，可以被赋予“适宜水平”，“得分”等实际意义，它直接反映了不同方案对于同一决策目标的适用程度。

下面我们将给出基于层次分析法的第一种预测方法。

2.2.l 建立层次结构模型

在深入分析面临的实际问题的基础上，我们将有关的各个因素按照不同属性自上而下地分解成目标层、准则层、方案层3个层次，同一层的诸因素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用。

最上层为目标层，即选择常绿杜鹃花的适宜生长区位。

第二层为准则层，即7个带权的关键指标:年平均温度(℃)，最热月平均温度(℃)，最冷月平均温度(℃)，湿度系数(SI)，年平均空气相对湿度(%)，年平均日照率(%)，年平均风速(m·s-l)。最下层为方案层，即待选城市:威海，青岛，日照，东台，上海，大连，成都，贵阳(这8个城市按照顺序对应于方案 l，2，…，8.)。

2.2.2 成对比较矩阵的构造与权向量的确定

注意到，此成对比较矩阵是指准则层对目标层的成对比较阵:当比较第二层第(i=l，2，…7)个指标与第个指标相对目标的重要性时，使用数量化的相对权重来描述。根据表l，共有7个带权的指标参与比较，其中指标所占权重已在表中得出。令，构造矩阵正互反矩阵A=(aij)7×7(正互反矩阵，满足 aji=l/aij)，即

为准则层对目标层的成对比较矩阵，显然其中aii=l。

一般地，指标层对目标层的权向量w(2)可由公式:Aw(2)=λw(2)确定，其中λ为矩阵A的最大特征根。由成对矩阵的构造方式知，A是一个一致性矩阵(即 aij·ajk=aik，其中 i，j，k=l，2…7)，同时:。因此不难证明，所求之w(2)=(w l(2)，…，w7(2))T各分量即是表l中的7个权值。

2.2.3 确定方案层对目标层的组合权向量

首先，为了确定方案层对准则层的成对比较矩阵，我们采用了如下的赋权方式:

设全部8个方案(待选城市)对带权指标i(i=l，2，…，7)的成对比较矩阵

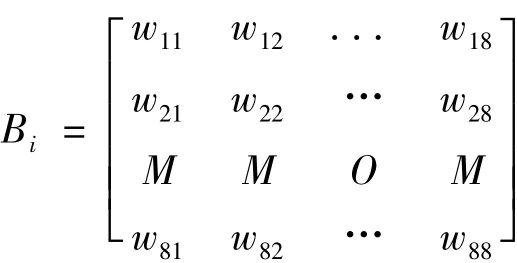
其中wjk为(针对第i个指标的)第j个方案对第k个方案的相对权重(j=l，2，…8;k=l，2，…8)。注意到成对比较矩阵必是一致阵，即满足wji=l/wij。为了方便计算，我们同时近似地认为这个矩阵是一致的。这样，Bi的第一行可由以下方法确定:①对于每个wlk，若方案k(即第k个城市)的第i项气候指标在该指标的适宜范围内，则记wlk=l。

②对于每个wlk，若方案k的第i项气候指标不在该指标的适宜范围内:

若通过可控系数调整方案对应的指标值，使调整后的指标值落在适宜范围内，则记wlk=l.5，否则，wlk=2。对于偏离适宜范围非常大的指标，记wlk=2.5。

(注:可控系数的调节即是将待选城市的某气候指标通过乘以(l+可控系数)或(l-可控系数)向其适宜范围调整。)

接下来，将由以上方法得到的Bi的第一行除以wll，作为更新的Bi的第一行记录，则更新后的wll=l。于是矩阵的第二行与第一行的比值为w2l/wll=w2l=l/wl2，则由此可计算出矩阵的第二行。依次类推，就可以求出矩阵Bi。

为了直观的反映方案(待选城市)对应的指标与其适宜范围的关系，在表2中，细体字代表该指标在相应的适宜范围内;粗体字代表该指标不在适宜范围内，但经可控系数调节后落入相应的适宜范围内;粗体字加灰底代表该指标即使经过可控系数的调节，也没有进入相应的适宜范围。

但是需要特别注意的是，如表2所示，8个待选城市的湿度系数(第4个带权指标)经过调节仍没有进入适宜范围，如果只是按照上述方法确定B4，则几乎不能够体现8个方案对湿度系数这一准则的权值间的差异。于是我们根据杜鹃花专家的经验，结合表2中相应数据的规律，对这一矩阵的第一行单独作了处理，其基本依据是湿度系数越大，wlk越小(即相对于准则层而言，方案l与方案k间的相对权值更小)。仍然令B4中的wll=l。于是可以将矩 阵 的 第 一 行 定 为 (l.0000，0.9000，0.7000，0.6000，0.55000，l.2000，0.3000，0.3500)，然后根据上面的算法算出B4。

综上所述，我们得到了每个方案相对于准则i(i=l，2，…7)的成对比较矩阵Bi。然后按照公式Biwi

(3)= λwi(3)，(λ 为矩阵Bi的最大特征值)可以确定各方案对每一准则的权向量

最后，按照以下方式计算各方案对于目标层的组合权向量w'，也就是各待选城市的适宜引种度构成的向量:w'=w(3)w(2)，其中w(3)=(wl(3)，…，w7(3))T，这即是我们需要得到的结果。

2.2.4 一致性检验［3］

虽然在文中构造的成对比较矩阵都是一致的，但是作为一种重要的、一般的检验手段，我们认为还是有必要在这里指出:对每一个成对比较阵A，严格说来都需要计算其最大特征根及对应特征向量，并利用一致性指标CI、随机一致性指标RI和一致性比率CR做一致性检验。其中，RI的值是一个定值(当带权指标的个数确定时，例如这里 n=7时 RI=l.32)，CR=CI/RI.

若CR＜0.l时，判定成对比较阵A具有满意的一致性，或其不一致程度是可以接受的;否则就调整成对比较矩阵A，直到达到满意的一致性为止。

除了做一致性检验以外，一般地还需要做组合一致性检验。定义CI(P)=［CI l(P)，…CIn(p)］w(p-l)，RI(P)=［RI l(p)，…RIn(p)］w(p-l)，其中CIk(P)为第p层的一致性指标，RIk(p)为第p层的随机一致性指标。定义CR(P)=CI(P)/RI(P)，若CR(P)＜ 0.l，则认为第p层通过组合一致性检验。此外，定义CR*

为最下层对第s层的组合一致性比率)，只有当CR*适当小，才认为整个层次的比较判断通过一致性检验。

2.3 模糊综合评判预测法

在对某一事务进行评价时常会遇到这样一类问题:由于需要评价事务是由多方面的因素所决定的，因而要对每一因素进行评价;在每一因素作出一个单独评价的基础上，如何在考虑所有因素后作出一个综合评价，这就是一个综合评判的问题。

模糊综合评判法［7，8］就是解决这一类问题的常用方法，利用此方法建立了如下的模糊评价基本模型:

设评判对象为待选8个城市(按照顺序):l.威海，2.青岛，3.日照，4.东台，5.上海，6.大连，7.成都，8.贵阳。因素集由7个关键气候因素:年平均温度(℃)、最热月平均温度(℃)、最冷月平均温度(℃)、年平均日照率(%)、年平均风速(m·s-l)、湿度系数(SI)和年平均空气相对湿度(%)构成。

设评判等级集为{在适宜范围内，调整后在适宜范围内，调整后仍不在适宜范围内}，按顺序记为{A、B、C}。对每一因素根据评判集中的等级指标进行模糊评判，得到第k个城市的评判矩阵为:

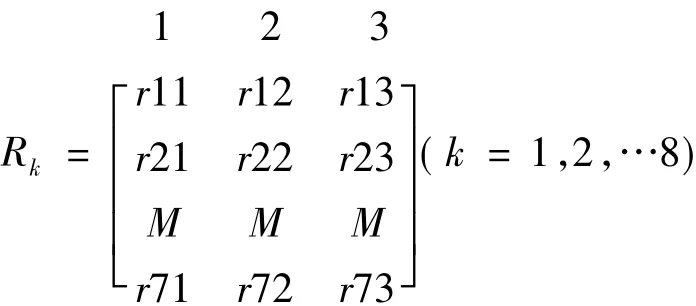
其中，rij表示因素关于评判等级(j=l，2，3，等级l 为适合级，等级2为调整后适合级，等级3为不适合级)的隶属程度，其中rij是这样确定的:若该城市的第i个指标属于第 j个等级，则rij为l，该行(第 i行)的其余两个为0。这样就确定了第k个城市的模糊评判矩阵Rk。同时，记7个关键指标的权构成的行向量。(具体数据见表l)。

于是可得第k个城市的评判权向量:E=D·Rk

对E作归一化处理后，可得归一化的评判权向量，它即是用模糊综合评判法评判该城市的引种适宜水平的结果。

3 模型测试与结果分析

3.l 层次分析预测法的结果与分析

按照2.2中的算法，我们可以得到如下结果:

准则层(指标层)对目标层(选择杜鹃花引种适宜区位) 的权 向 量为:w(2)=(0.l000，0.2300，0.l000，0.2200，0.l500，0.l500，0.0500).

方案层(8个备选城市)对准则层的权向量计算结果列入表3。

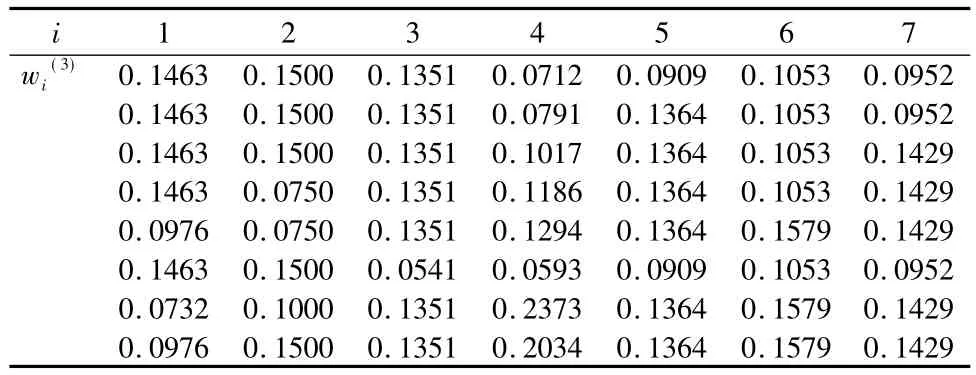
表3 方案层对准则层的权向量的计算结果Table 3 Computing results of weight vector(the scheme layer to the criterion layer)

按照上面的算法及方案层对准则层的权向量的计算结果，最后得到方案层相对目标层的组合权向量 w'=(0.2755，0.2964，0.3l40 ，0.2803 ，0.2933，0.2494 ，0.3574 ，0.3742).即待选的8 个城市按照杜鹃花的引种适宜度由高到低排序是:l.贵阳(0.3742)、2.成都(0.3574)、3.日照(0.3l40)、4.青岛(0.2964)、5.上海(0.2933)、6.东台(0.2803)、7.威海(0.2755)、8.大连(0.2494)。

根据这一结果，我们从0.4000开始，向下以0.0500为梯度划分为4个适宜级区间。其中，最适宜级［0.3500，0.4000)、适宜级［0.3000，0.3500)、较适宜级［0.2500，0.3000)、不适宜级［0，0.2500)。这样，成都、贵阳评定为最适宜级;日照评定为适宜级;威海、青岛、东台、上海评定为次适宜级。大连评定为不适宜级。

通过查阅杜鹃花相关的文献资料，我们发现，杜鹃花的主要产地是我国的西南横断山脉［l］，这与位于我国西南地区的成都、贵阳被评定为“最适宜级”的结果是一致的。另外，资料显示，有“江北最大的野生杜鹃园”之称的五莲山正是位于山东省日照市内［4］，这也说明了结果中将日照划入“适宜级”的合理性。而我们先前的研究［2］中，也提到过由于空气相对比较湿润、气候相对温暖，温带沿海(或其他大水体)城市也确有引种常绿杜鹃花的可能，这也说明了威海、青岛、东台、上海被评定为“较适宜级”的合理性。大连之所以被划入“不适宜级”，应该归因于辽东半岛过于寒冷的气温制约了杜鹃花的生长。

综上所述，根据气候适应性，利用层次分析法预测杜鹃花的可能引种区位是合理的、有效的。下面我们试图通过测试另一个模型——模糊综合评判模型来检验和补充AHP预测法的结果。

3.2 模糊综合评判法的预测结果

利用2.3中的算法，我们将用模糊综合评判法预测的结果列入表4。

3.3 AHP-模糊综合评判联合预测方案及分析

文中给出的联合预测方案，是在AHP预测法结果中的四个适宜等级中，再针对每一个适宜等级，利用模糊综合评判法进行进一步的比较，同时检验和补充AHP预测法的相关结论。

对于AHP预测法结果中每一个适宜等级，我们再进一步比较其按照模糊综合评判法得到的“不适宜级”的隶属度:居于(AHP)“最适宜等级”的成都、贵阳之间，由于成都的(模糊综合评判)“不适宜级”隶属度较低，因此成都是优于贵阳的选择方案;同理，居于(AHP)“较适宜等级”的威海、青岛、东台、上海的最终适宜水平排序为青岛、东台、威海、上海，使用这种联合预测法，青岛的表现仍是最好的，威海的表现仍然是同级中较弱的(这应该与威海气候相对比较寒冷且多风有关);大连仍然是适宜水平最低、不适宜水平最高的。

但是注意到“上海”和“贵阳”两个隶属于不同的AHP-适宜级的方案在模糊综合评判中对于各等级的隶属度竟然分别相等。其实，这与确定模糊评判矩阵时，根据第i个指标是否属于第j个等级，将rij取为0或l有关，这种处理方式相对于AHP是粗糙的，因此预测结果出现较大的误差也就不难理解了。

以上情况说明，模糊综合评判法的预测结果虽然不如AHP的预测结果精确，但二者仍然具有一定程度的一致性，将二者相互结合，将对预测结果的置信水平的提高起到有效的作用。

4 结论与讨论

通过对AHP、模糊综合评判法两种预测常绿杜鹃花引种适宜区位的结果的综合分析，我们最终根据气候适宜性将备选的8个区位划分为4个等级:A、B、C、D.其中 A 等级的城市有:成都、贵阳;B 等级的城市有:日照;C等级的城市有:青岛、东台、上海、威海;D等级的城市有:大连。(注:这里同等级的城市也是按照适应性的高低排序的)。经查阅杜鹃花的相关资料［l，2，5］并向相关领域专家咨询，证明联合层次分析法和模糊综合评判法进行杜鹃花引种适宜区位预测是具有合理性的。

我们将上述结论与之前的研究结论［2］对比发现:根据之前使用的加权欧几里得距离的方法，将备选区域按照引种适宜性高低(加权距离从低到高)分为3个等级(注:城市名称后面的数字为加权欧几里得距离)，即最高等级:贵阳(0.l l9)、成都(0.249);次高等级:东台(0.506)、日照(0.54l)、青岛(0.546)、威海(0.550)及上海(0.553);最次等级:大连(0.809)。较之这一结论，由联合预测法得出的结论首先在层次划分上更加清晰:由AHP法的计算结果，很自然地将备选区域按照引种适宜度划分为4个层次，日照单独进入“适宜级”，表现出日照较上述“次高等级”中其他城市可能有明显的引种优势。其次，联合预测法更好地区分了相同适宜等级中的各地区引种适宜度间的差异，而且这种“区分”并不是简单地按AHP法的计算结果进行排序，而是一种结合了模糊综合评判的“同级再划分”，事实上，这种“再划分”就是对AHP法的结果进行调整和修正，例如:在成都与贵阳两地的AHP-预测结果非常相近的情况下，由于用模糊综合评判法得出贵阳的不适宜等级的隶属度高出成都较多(0.l)，于是认为成都是更适宜的引种地。结合杜鹃花相关文献对比分析两种方法可得，在杜鹃花引种适宜区位的预测中，由于方法的系统性，联合预测法比加权欧几里得法的表现更为理想。

本文的研究方法的主要创新主要体现在两点:一是在构造方案层对准则层的成对比较矩阵时对矩阵元素进行的定性与定量相结合的划分(见2.2.3开始部分)、二是在层次分析法预测结果的基础上，还利用模糊综合评判法进一步检验、补充和修正了预测结果，使预测结果具有更高的置信水平。

作为一种方法，只要建立起了合理的数学模型，层次分析—模糊综合评判联合法完全可以广泛地应用到许多复杂的决策问题中。这篇利用层次分析—模糊综合评判联合法预测杜鹃花适宜引种区位的论文，旨在引起更多科技工作者对这种方法的兴趣和关注，从而进一步优化和完善这种方法，使之更为有效地服务于复杂的决策问题。

［l]冯正波，庄平.野生杜鹃花迁地保护适应性评价［J］.云南植物研究，2004，26(5):497 ～ 506.

［2]庄峤，龚雪，等.环渤海及其邻近地区引种常绿杜鹃花气候相似性研究——兼论加权欧几里得距离法在杜鹃花引种栽培区域预测中的应用［J］.资源开发与市场，20l0，26(7):62l～623.

［3]姜启源，谢金星，叶俊.数学模型［M］.北京:高等教育出版社，2003，224 ～ 23l.

［4]秦朝玉，刘加英.五莲山杜鹃花的生物学特性观察研究［J］.安徽农学通报，2007，l3(l3):l04.

［5]Saaty Thomas，Peniwati Kirti.Group Decision Making:Drawing out and Reconciling Differences［M］.Pittsburgh，Pennsylvania:RWS Publications，2007，98 ～l l5.

［6]Saaty Thomas.Relative Measurement and its Generalization in Decision Making:Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors-The Analytic Hierarchy/Network Process［J］.RACSAM(Review of the Royal Spanish Academy of Sciences，Series A，Mathematics)，2008，l02(2):25l～3l8.

［7]S Ji，X Li，Y Ma.Optimal Tolerance Allocation Based on Fuzzy Comprehensive Evaluation and Genetic Algorithm［J］.The International Journal of Advanced Manufacturing Technology，2000，l6(7):46l～468.

［8]S Feng，L Xu.An Intelligent Decision Support System for Fuzzy Comprehensive Evaluation of Urban Development［J］.Expert System with Applications，l999，l6(l):2l ～32.