制导弹药允许发射区参数模型设计

左伟，冯金富，张佳强

(空军工程大学 工程学院，陕西 西安710038)

0 引言

制导弹药的开发者正致力于研究如何以较低的成本将制导弹药集成到不同的载机平台以增加其互用性。如美国军方已成功地将联合直接攻击弹药(JDAM)集成到空军和海军10 余种型号的飞机上，其它制导弹药的互用性试验也正在进行中。要想降低制导弹药的集成成本就必须尽量减少集成对载机作战飞行程序OFP 的影响［1］。武器的允许发射区(LAR)计算程序作为OFP 重要的组成部分，其计算的复杂度直接影响武器的互用性。

目前，存在多种制导弹药的LAR 算法。如6 自由度(DOF)模型法、快速模拟法、模糊法和神经网络法等，6DOF 模型法和快速模拟法是以解算武器的运动方程、武器结构模型、大气环境条件等数学模型或其简化形式为基础的。该方法可以获得高精度的LAR，但需要较多的计算资源且不适合于实时应用;模糊法和神经网络法采用函数逼近器对武器6DOF 模型的输出进行匹配，在一定程度上减轻了计算负担。但由于模糊系统和神经网络的结构比较复杂，要拟合的参数比较多，解算程序的软件实现复杂，特别是当模糊系统的模糊规则数和神经网络的计算神经元较多时，不但会影响解算结果的实时性，而且当要把制导弹药集成到不同的载机平台时，需对OFP 中的解算程序作较大的修改。为促进制导弹药的互用性，美国空军武器系统评审执行委员会(EWSR)向汽车工程师协会(SAE)请求协助，希望设计一种新的LAR 算法，来支持制导弹药在不同载机平台之间的“即插即用”集成［2］。SAE 提供的建议之一是要设计一种LAR 的参数模型，使武器或飞机制造商能够通过更新参数来实现武器性能的改进。

本文提供了一种LAR 参数模型的设计方法，该方法采用一组二次多项式来建立LAR 几何形状参数的数学模型，通过仿真实验获得模型系数的训练数据集和验证数据集，利用多元回归来拟合模型的系数。拟合的参数模型使用一组二次多项式来匹配制导弹药6DOF 模型的输出而并非实际地建模制导弹药的运动方程组，这样就可以避免由解算武器的6DOF 模型所带来的计算负担，使之适应于实时应用，而且可以通过更新模型系数来支持制导弹药在不同载机平台之间的实时集成。

1 LAR 参数模型的建立

LAR 是定义在空间中的一个区域，在该区域内发射的武器可以成功地导向目标。通常，LAR 为空间中的一个非规则的几何区域，载机利用一个数学模型来计算并显示该几何区域的一个近似，该数学模型即为LAR 算法［3］。为建立LAR 算法的数学模型，首先对LAR 几何形状作出以下基本设定:

1)参考坐标系为地面固定坐标系。原点以发射时刻的载机为中心，x 轴的正向指向载机速度矢量的水平分量，y 轴在水平面内与x 轴垂直且指向右为正，z 轴由右手定则确定(与美国军用标准MILSTD-1760 规定的坐标系一致)。LAR 即为该坐标系xy 平面内的一个几何形状。

2)LAR 的几何形状用一个n(n≥5)顶点的多边形来表示，多边形顶点的数目可根据武器具体的LAR 性能要求确定。多边形的参考点在参考坐标系中的坐标为(xr，yr).

3)多边形的第一个顶点v1定义在通过参考点(xr，yr)与x 轴平行的线上且距参考点r1处。

4)各顶点的标号相对于第一个顶点沿顺时针方向依次递增。相邻顶点与参考点连线之间的夹角均为(360/n)°.

5)顶点vi定义在通过参考点且与x 轴正向夹角为(360 ×(i-1)/n)°的线上且距参考点ri处。

一个任选的8 顶点多边形所表示的LAR 实例如图1所示。

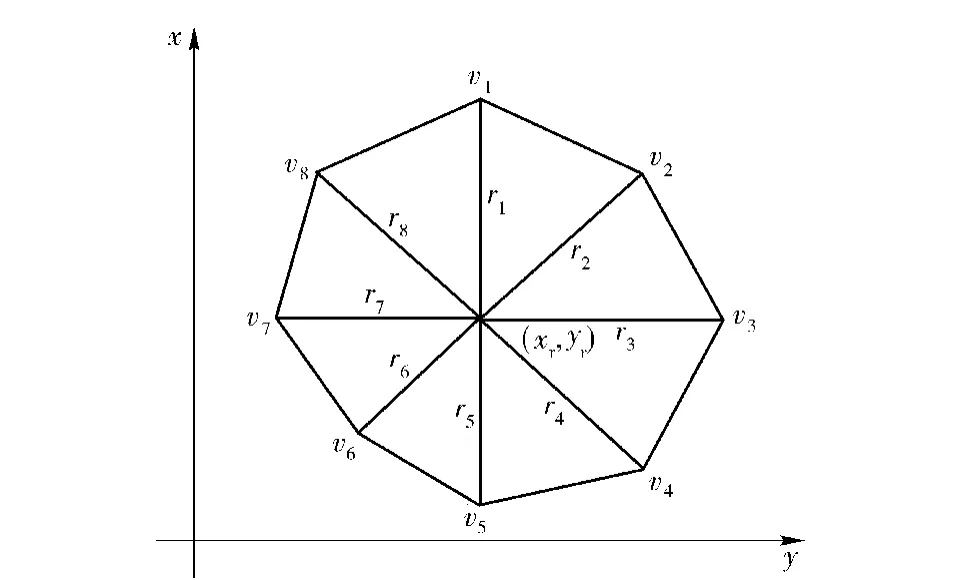
图1 多边形表示的LARFig.1 LAR represented by polygon

基于以上基本设定可知，该多边形的形状和大小由参考点和各顶点在参考坐标系中的坐标所确定，而参考点和各顶点的坐标依赖于影响武器LAR形状和大小的因素，如载机的速度v、载机到目标的高度h 和风速wv等，因此，可将该多边形各确定点的坐标xr，yr，x1，y1，… ，xn，yn作为模型的依赖变量，将影响武器LAR 形状和大小的因素作为模型的独立变量，建立各确定点坐标的数学模型如下:选择二次多项式作为fj(1≤j≤k，k=2n+2)的数学形式，于是，这组二次多项式方程即为LAR 的参数模型。理论上(1)式中的任一方程fj将由m 个项组成，这m 个项的系数组成一个系数向量(cn1，cn2，…，cnm)，所有方程的系数向量组成一个系数矩阵Ck×m，因此该参数模型又可称为基于系数的LAR算法［3］。接下来的问题就是如何确定系数矩阵Ck×m.

2 基于RSM 的模型系数的确定

反应曲面建模(RSM)是数学和统计技术的综合，它主要根据实验来研究一个或多个观测的反应与多个输入因素之间的关系。它包括以下几个部分:设计一组实验、建立一个数学模型来抽象感兴趣的反应与其影响因素之间的关系、基于该数学模型确定感兴趣的反应的最优值来更好地理解系统的整体行为［4］。这里感兴趣的反应为多边形各确定点的坐标xr，yr，x1，y1，…，xn，yn影响因素为独立变量v，h，wv等。根据RSM 原理，确定系数矩阵Ck×m的大致过程如下:首先设计一组仿真实验来获得一组各坐标点的观测值即训练数据集，然后通过对训练数据集进行多元回归分析获得各系数的估计值，并通过方差分析和假设检验对拟合的结果进行检验，这样就得到一个初始的系数矩阵。最后，设计另一组仿真实验产生一组独立的验证数据集来对初始的系数矩阵作进一步验证，以获得“验证的LAR 系数”［2］。

2.1 基于D-最优设计的训练数据集的产生

训练数据集主要用于拟合LAR 参数模型。为了产生训练数据集，必须设计一组仿真实验，通过武器的6DOF 模型获得一组较精确的LAR 观测值。为了在较少的实验内提高拟合的精度，这里采用D-最优设计［5］来设计实验点集。

假设某制导弹药的6DOF 模型有m 个输入，则实验数据空间可定义为

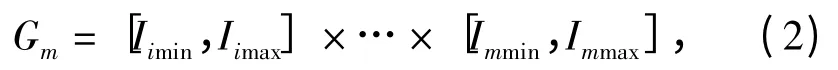
式中Iimin和Iimax分别为第i 个输入变量取值的下限和上限。

要拟合的参数模型为二次多项式，如下式所示:

式中:xi为独立变量;ε 为随机误差且服从正态分布ε～N(0，σ2).假设Y 是由所有反应组成的p 维向量，表示成矩阵形式为

式中:Y=［yn1，yn2，…，ynp］T;b=［b0，b1，…，

拟合的目标就是要使模型系数估计的置信椭球体的体积最小化。根据最小二乘拟合原理［6］，模型系数的估计为

系数的协方差矩阵为

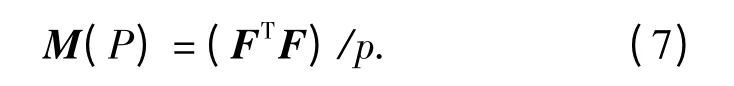
D-最优设计就是要设计实验点集P 使信息矩阵M(P)的行列式达到极大。

寻找最优实验点集是一个在实验数据空间内寻优的过程，这里，基于DETMAX 算法［7］来寻找最优的实验点集，过程如下:

1)随机选择一个n ×m 的初始设计矩阵F，并计算f(F)=det(FTF);

2)寻找所有以F 为子矩阵的(n+1)×m 的可行设计矩阵的集合S，其中S 中的任一元素H 是通过在F 中增加一个可行设计点得到的;

3)在S 中寻找最优元素Hi构成的子集S'，其中

4)寻找S'中的所有元素的所有n ×m 子矩阵F'构成的集合T.

5)在T 中寻找最优元素F'i构成的子集T'，其中

6)对T'中的每一元素重复算法过程;

7)比较每次迭代产生的F'i与该次迭代的初始设计Fi的函数值，如果f(F'i)≤f(Fi)，停止算法并返回最优设计Fi，否则继续。

通过该算法可获得一组离散的实验点集，在这些实验点上运行仿真实验便可获得训练数据集，再通过多元回归便可拟合出各二次多项式的系数。为了消除武器6DOF 模型各输入值的数量级不同对拟合精度的影响，在拟合之前，需对各独立变量进行编码处理，编码公式如下:

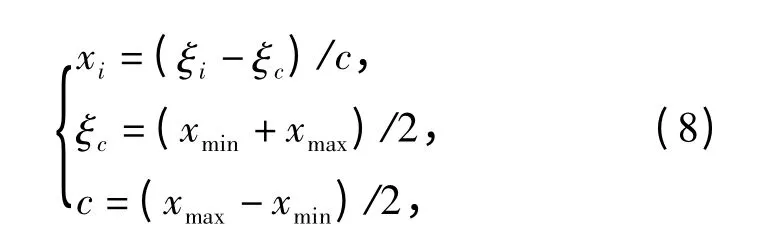
式中xi、ξi、ξc和c 分别表示变量的编码值、变量的原始值、变量取值区间的中心点和步长。

2.2 基于Sobol 序列的训练数据集的产生

为了确保从训练数据集得到的系数在整个武器发射条件包络内都满足性能需求，必须用一组独立的验证数据集来对系数进行验证。验证数据集对应的实验点集同样取自实验数据空间Gm，但取自不同的点。为了确保验证的充分性，实验点集必须具有较好的空间均匀分散性。评价数据点集空间均匀分散性好坏的指标之一是偏差［8］，定义如下:给定一个点集x1，x2，…，xN∈Gm和一个子空间G∈Gm，定义计数函数SN(G)为该点集中位于子空间G 中的点(xi∈G)的数目。对每一个x=(x1，x2，…，xm)∈Gm，令Gx=［0，x1)×［0，x2)×… × ［0，xm)为体积为x1x2…xm的m 维矩形体，则点集x1，x2，…，xN的偏差定义为

偏差D 越小，则点集的空间均匀分散性越好。基于伪随机序列产生的实验点集比随机选择的实验点集具有更好的空间均匀分散性，这里基于Sobol伪随机序列［9］来设计验证数据集对应的实验点集。首先产生一个m 维的Sobol 序列，然后Sobol 序列的每一元素都对应实验数据空间的一个采样点。产生一维Sobol 序列的步骤如下:

1)选择一个Z2域的d 阶本原多项式P=xd+a1xd-1+…+ad-1x+1，ai=0，1.只要P 是本原的，多项式可任意选择。

2)设置m1，m2，…，md的值。只要满足mi为奇数且mi＜2i，则mi的值可任意选择。然后根据(10)式计算md+1，md+2，….

式中⊕表示二进制位的异或运算。

3)通过(11)式产生一组方向数v1，v2，….

4)通过(12)式产生序列x1，x2，…，xN.

式中bk…b3b2b1是n 的二进制表示。

要产生m 维的Sobol 序列，只需选择m 个不同的本原多项式并计算m 组不同的方向数，然后使用对应的方向数来计算每一维的元素即可。

利用Sobol 序列产生一组实验点集，通过仿真实验便可获得验证数据集。然后利用训练数据集拟合的LAR 参数模型计算得到一组LAR 的预测值，并将它与验证数据集进行比较，如果结果满足预定的LAR 性能标准，则设计结束。否则，必须通过增加实验点来重新获得一个更大的训练数据集。LAR模型系数的训练是一个迭代的过程，在设计中，需要根据验证结果不断地增加训练数据，直到获得满意的系数为止。

3 实例分析

下面用一个假想的激光制导炸弹为例来验证该设计方法。该激光制导炸弹的LAR 用一8 顶点的多边形(见图1)来表示，其LAR 仿真实验利用的6DOF 模型见文献［10］。仿真实验定义的独立变量及其范围和水平如表1所示。

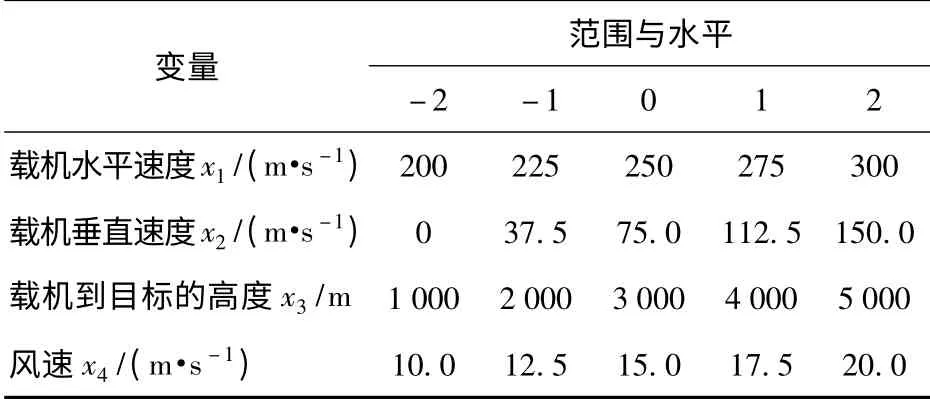
表1 独立变量的范围与水平Tab.1 The ranges and levels of independent variables

从表1可知实验的数据空间为G4=［200，300］×［0，150.0］×［1 000，5 000］×［10.0，20.0］.基于D-最优设计在数据空间G4内选择一组最优的实验点集并通过仿真实验获得一组LAR 系数的训练数据集，通过多元回归拟合出多边形各参数的数学模型。下面，选择参数xr来对结果进行分析。拟合得到编码后的xr的二次多项式模型为

利用方差分析和多元回归分析对(13)式的拟合结果进行评估。模型方差分析的结果如表2所示。

模型的总体回归质量可通过F 检验及对应的P值来评估，F 值越大且P 值越小，表明模型的总体回归质量越好。从F 检验的结果(Fm=13 390)和接受零假设(模型系数都为0)的概率(P=0)可以看出，该回归模型是显著的。R2是模型的确定系数，它用于评价模型的输出与独立变量的相关程度。从R2值(R2=0.995)可知只有5%的输出偏差不能被模型所解释，这表明输出xr与独立变量之间具有高度的相关性。各个系数的回归分析如表3所示。采用的假设检验为基于学生分布的t 检验，零假设为单个系数为0(bi=0)，显著性水平为0.05.从各系数对应的t 值可以看出回归模型的各系数是显著的。

表2 回归模型的方差分析Tab.2 Variance analysis of regression model

表3 各系数的回归分析Tab.3 Regressive analysis of coefficients

接下来，用一组独立的验证数据集对拟合得到的系数进行测试。验证数据集对应的实验点根据一个4 维Sobol 序列来采样，产生该Sobol 序列的4 个本原多项式为

参数xr的实验观测值和模型预测值如图2所示。

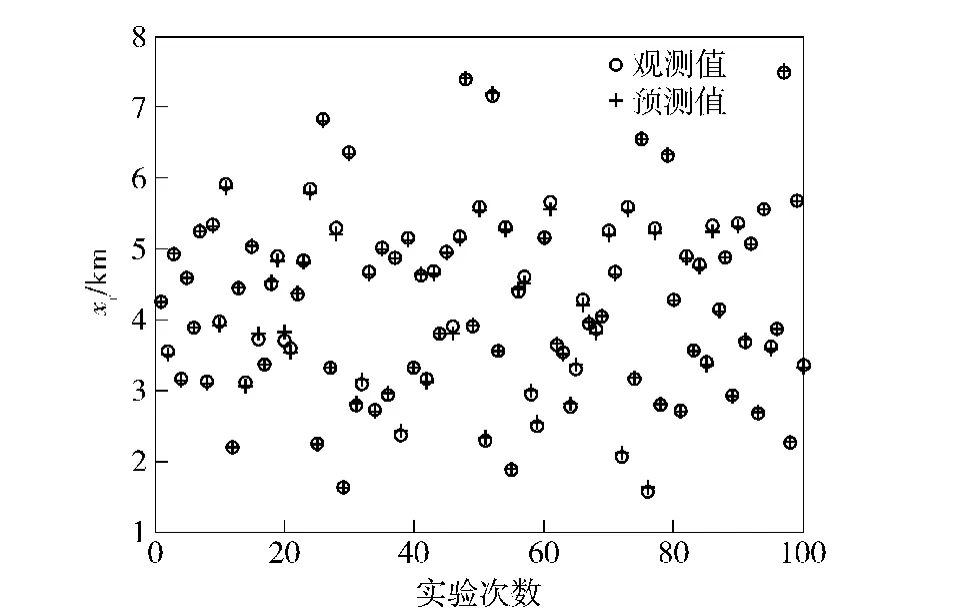
图2 xr的验证值和预测值Fig.2 The verification data and predicted values of xr

从图2可以看出xr的观测值和预测值具有合理的一致性，这表明xr的模型对应的系数是可用的。同理，可对其它参数yr，x1，…，y8的模型系数进行验证。最后，所有多项式的系数组成一个矩阵C18×15，该系数矩阵即为“验证的LAR 系数”。

最后，基于“验证的LAR 系数”对LAR 的解算精度进行评估。评估指标为失去发射机会概率Pml、界外发射概率Pob和成功发射概率Psl，要求平均成功发射概率大于85%.计算示意图如图3所示。

图3 LAR 解算精度的评价指标示意图Fig.3 Evaluation index of LAR calculation precision

根据图中的近似投放区Af、参考投放区Am及它们的重叠区Ac，各评估指标的计算公式如下:

失去发射机会概率:

界外发射概率:

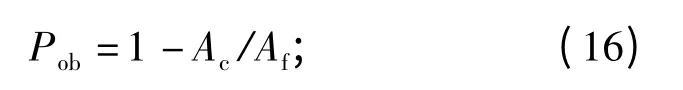
成功发射概率:

分别采用“验证的LAR 系数”来计算近似投放区Af及文献［10］中的6DOF 模型来计算参考投放区Am，并根据(15)式～(17)式来计算上述评价指标，统计得到的各评价指标为:Pml=6.87%，Pob=5.39%，Psl=88.12%.从该统计结果可以看出，采用“验证的LAR 系数”解算的LAR 在可接受的范围之内。

4 结论

制导弹药允许投放区解算的实时性和精确度对其作战效能的发挥起着至关重要的作用。本文定义了一个n 顶点的多边形来表示制导弹药LAR 的几何形状，建立了计算其LAR 的数学模型，并设计了模型系数的训练数据集和验证数据集产生方法，其中基于D-最优设计的训练数据集产生方法可有效地减少仿真实验的次数和提高模型系数估计的精度，基于Sobol 序列的验证数据集产生方法可确保系数验证的充分性。“验证的LAR 系数”可用于在线解算制导弹药的允许投放区，提高LAR 计算的实时性。设计的参数模型结构简单，有助于降低解算程序的计算复杂度。然而，由于拟合误差的存在，该方法解算的LAR 精确度要低于6DOF 模型法，但仿真实验结果表明仍在可接受的范围之内。

References)

［1］ Common launch acceptability region approach interface control document，SAE aerospace information report AIR5682［R］.US:Society of Automotive Engineers，2007.

［2］ Common launch acceptability region (CLAR)truth data generator interface control document(ICD)for the CLAR approach (CLARA)，SAE aerospace information report AIR5788［R］.US:Society of Automotive Engineers，2005.

［3］ Common launch acceptability region approach (CLARA)rationale document，SAE aerospace information report AIR5712［R］.US:Society of Automotive Engineers，2008.

［4］ Lin J F，Chou C C.The response surface method and the analysis of mild oxidational wear［J］.Tribology International，2002，35:771-785.

［5］ 富立，刘文丽.D-最优试验设计在动力调谐陀螺测试中的应用［J］.航空学报，2008，29(2):467-471.FU Li，LIU Wen-li.Application of D-optimal test design method in testing of dynamically tuned gyroscope［J］.Acta Aeronautica et Astronautica Sinica，2008，29(2):467-471.(in Chinese)

［6］ 王惠文，孟洁.多元线性回归的预测建模方法［J］.北京航空航天大学学报，2007，33(4):500-504.WANG Hui-wen，MENG Jie.Predictive modeling on multivariate linear regression［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(4):500-504.(in Chinese)

［7］ Michael G Neubauer，Richard G Pace.D-optimal (0，1)-weighing designs for eight objects［J］.Linear Algebra and its Applications，2010，432:2634-2657.

［8］ Fang K T，Lin D K J，Winker P.Uniform design:theory and application［J］.Technometrics，2000，42:237- 248.

［9］ Cumber P S.Accelerating ray convergence in incident heat flux calculations using Sobol sequences［J］.International Journal of Thermal Sciences，2009，48:1338-1347.

［10］ 王庆江，高晓光.激光制导炸弹的仿真及其有效投弹区的计算［J］.火力与指挥控制，2008，33(8):44-47.WANG Qing-jiang，GAO Xiao-guang.Simulation and calculation of effective attack area about laser-guided bomb［J］.Fire Control and Command Control，2008，33(8):44-47.(in Chinese)