超分辨谱估计法在测速雷达中的应用

谭渊，杨勇，袁乃昌

(国防科学技术大学 电子科学与工程学院 微波中心，湖南 长沙410073)

近年来，国内部分靶场利用连续波多普勒测速雷达，通过在弹丸底部刻槽来测试弹丸的转速。这种测试方法相比于早期的纸靶法和高速摄影法［1］，可以得出弹丸飞行过程中转速与时间的实时曲线，而且测试精度更高。其基本原理就是从目标的回波信号中估计出弹丸多普勒频谱以及由于刻槽引起的调制谱，进而计算出弹丸转速。精确测量旋转弹丸的转速，对于弹丸的气动设计、空气动力学研究或是武器射表编拟中的弹道计算，都具有十分重要的意义。

因此，如何尽量精确估计回波信号的频谱是决定转速测量误差的关键。本文在详细分析弹底刻槽法的基础上，引入超分辨谱估计的旋转不变算法，代替了传统FFT 对回波信号进行处理，进一步提高实验测试精度。

1 旋转不变子空间法

在雷达信号的处理过程中，传统的方法是采用FFT 对信号进行频谱估计，该方法的频率分辨率受不相容原理限制，是一种低分辨的谱估计方法。本文采用基于旋转不变空间(ESPRIT)模型的谱估计方法，通过对系统传递函数进行特征分解而得到信号的估计谱。而传递函数的估计可以通过直接数据近似方法得到，即对数据矩阵进行奇异分解估计传递函数，该方法可同时计算得到其信号分量对应的复幅度。

假设信号y(n)包含p 个谐波信号

式中:si(n)和ωi分别为第i 个谐波信号的幅值和频率。假定ω(n)是一个0 均值、方差为σ2的高斯白噪声。旋转不变法状态模型的参数估计是通过对数据矩阵的分解而得到的，构造数据矩阵［2-5］:

式中:A=［a(ω1)，a(ω2)，…a(ωp)］;a(ωi)=［1，

令A1为矩阵A 的前(L-1)行，A2为矩阵A 的后(L-1)行，即

则根据等距线阵的阵列相应矩阵A 的结构可知，子矩阵A1和A2之间存在以下关系:

式中P=E{s(n)sH(n)}为信号向量的相关矩阵。由于故由(5)式易知

用Us右乘(6)式两边，注意到排，即得并加以重

式中T 为一个非奇异矩阵，

用T 右乘(3)式则有

采用相同的分块方式，将Us也分块成

由于Us=AT，故比较(9)式与(10)式，立即有

将(4)式带入(12)式，则

由(11)式及(13)式可得

定义

矩阵Ψ 称为矩阵Φ 的相似变换，因此它们具有相同的特征值，即Ψ 的特征值也为ejφm，m=1，…，M.

由此可以得出该方法的计算步骤:

2 转速测量的理论基础

2.1 底部刻槽弹丸的RCS 分析

在炮弹底部刻一直线槽。设S 为炮弹底部总面积，槽深为d，槽外的底部面积S1，则槽的面积为S2=S-S1.由于槽相对炮弹底部很窄，可以把槽作为终端短路的无限宽传输线来分析［6］，如图1所示。

图1 传输线分析模型Fig.1 Analysis model of transmission line

现假设雷达发射电磁波为Et=E0e-jkzzx，槽反射的电磁波在接收机处为

S2反射的电磁波在接收机处为

由场的叠加得，在接收机处的总场为

此时，当入射波垂直于弹丸底部、入射的电场与槽的方向垂直时，弹丸底部的总RCS 等于

而当入射波垂直于弹丸底部、入射的电场与槽的方向平行时，弹丸底部的总RCS 等于没有槽的底面RCS，即

2.2 刻槽弹丸的转速计算

假设刻槽弹丸的旋转频率为fr，当炮弹旋转一周，通过2.1 节弹底的RCS 变化分析可知，槽线2次与入射电场方向平行或者垂直，周期为π，因此而引起的RCS 变化规律(或者说是回波信号强度的变化规律)可以定义为对无刻槽弹丸多普勒频率的余弦调制，调制信号可表示为

雷达发射信号是单频连续波，对于未刻槽的弹丸，接收信号经过下变频得到的中频信号可以表示为

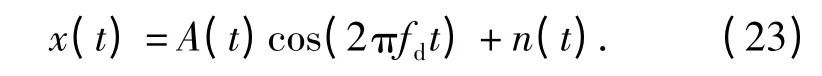
式中:A(t)为信号幅度随时间的变化关系;n(t)为白噪声。

弹丸底部刻槽之后，加上对多普勒频率的调制信号，则接收到的中频信号为

由于调制信号非常弱，故B(t)远小于A(t).带入B(t)并将(24)式展开可以得到:

得到fd、fd1=fd+2fr和fd2=fd-2fr三个频率，从而弹丸转速可以表示为:

因此，经过上述分析可知，精确测量弹丸转速可以转化成精确测量估计回波信号中的频谱值。

3 仿真计算

假设一个连续波信号由3 个不同频率成分和白噪声组成，表示为

式中:令f1、f2、f3分别等于90，100，110 Hz;n(t)表示幅度均值为0，方差为1 的高斯白噪声。然后在+20 dB 信噪比的情况下，利用经典FFT 算法对该信号进行频谱估计，结果如图2所示。然后再按照ESPRIT 法的步骤估计信号频谱，结果如图3所示。

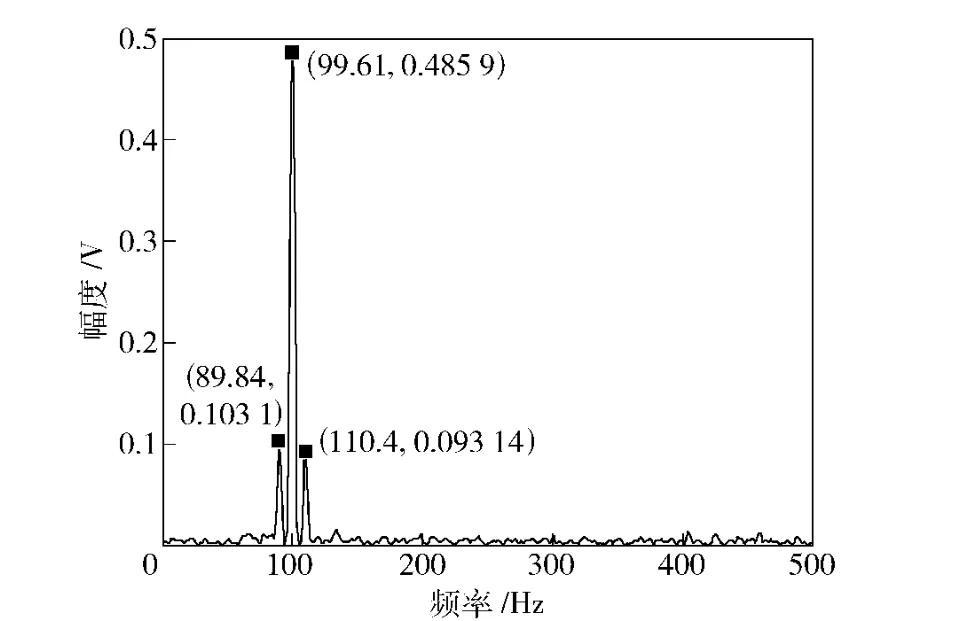
图2 20 dB 信噪比下的FFT 频谱估计Fig.2 FFT spectrum estimation under SNR=20 dB

表1计算比较了2 种估计方法的误差精度，结果表明，ESPRIT 法具有比FFT 法更高的估计精度，能够更精确的测量出炮弹的旋转速度。

超分辨谱估计的估计精度(分辨率)和信噪比成正比关系，由ESPRIT 法统计特性可知，较大信噪比情况下，单频信号频率估计均方误差

式中:σ2n为噪声方差;P 为信号功率。当取L=2N/3 时得到最小均方误差27σ2n/(4N3P)，接近Cramer-Rao下界6σ2n/(N3P)［6］.图4为在不同信噪比下2种算法的估计均方误差比较。可以看出，ESPRIT 法明显比FFT 算法具有更精确的频谱估计能力，而且随着信噪比的提高，ESPRIT 法的估计误差会愈小。而FFT 算法的频谱估计误差与信噪比没有直接联系，它只能依靠加大运算量、增加FFT 的运算长度来减少估计误差。

图3 20 dB 信噪比下的ESPRIT 频谱估计Fig.3 ESPRIT spectrum estimation under SNR=20 dB

表1 ESPRIT 法与FFT 法估法比较Tab.1 Comparison between ESPRIT and FFT

图4 不同信噪比估计频谱与实际频谱的均方误差Fig.4 Error between estimated and real spectrums under different SNRs

4 实测结果

利用某型号C 波段俯仰自跟踪连续波测速雷达雷达，如图5所示。测量弹丸相对于雷达天线的径向飞行速度和转速。实验弹丸为底部刻有7 道深为12.1 mm 槽的某型号榴弹。

图5 某型号C 波段速度测量雷达Fig.5 A C-band velocity-measurement radar

图6对不同时刻的回波信号的频谱归一化，并在同一个速度—时间轴上显示出其频谱瀑布图。

图6 回波信号的瀑布图显示Fig.6 Waterfall graph of echo signal

可以得到3 条多普勒曲线，中间的曲线幅值较大，为弹丸径向速度的多普勒fd，两边的曲线则是由刻槽引起的调制信号。通过估计各时刻的信号频谱值，提取出fd1、fd2，根据(26)式可以计算出弹丸的转速。

5 结语

运用超分辨谱估计法测量弹丸转速的方法是一种高精度测试方法。本文分析了旋转不变法估计原理，给出了ESPRIT 方法的估计步骤，该方法能高精度估计回波多普勒信号频谱，并通过底部刻槽对弹丸RCS 的影响推导出了转速计算公式。仿真结果表明，不同信噪比情况下，ESPRIT 法估计精度及分辨率明显优于经典FFT 法，而且其精度随着信噪比的提高而增加，这种现象是FFT 所不具备的。值得一提的是，提高回波信噪比一直是雷达工作者们改善系统性能的一个重要思路，所以ESPRIT 频谱估计法的这一性质也使得信噪比提高的同时，其频谱估计精度也相应提高。该高精度测量弹丸转速的方法具有广阔的应用前景。

References)

［1］ 金达根，任国民.实验外弹道学［M］.北京:兵器工业出版社，1991.JIN Da-gen，REN Guo-min.Experimental exterior ballistic theory［M］.Beijing:The Publishing House of Ordnance Industry，1991:31-134.(in Chinese)

［2］ 张贤达.现代信号处理［M］.第2 版.北京:清华大学出版社，2004.ZHANG Xian-da.Modern signal processing［M］.2nd ed.Beijing:Tsinghua University Press，2005:138-143.(in Chinese)

［3］ 王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京:清华大学出版社，2004.WANG Yong-liang，CHEN Hui，PENG Ying-ning，et al.Theory and algorithm of spatial spectrum estimation［M］.Beijing:Tsinghua University Press，2004:186-188.(in Chinese)

［4］ Rao B D，Hari K V S.Effect of spatial smoothing on state space methods/ESPRIT［C］∥Fifth ASSP Workshop on Spectrum Estimation on Modeling.Rochester:1990:377-381.

［5］ 王剑，吴嗣亮，侯淑娟.超分辨条件下雷达目标散射点数的估计方法［J］.电子学报，2008，36(6):1058-1062.WANG Jian，WU Si-liang，HOU Shu-juan.Detecting the scatterer number of radar target for SSM super re solution［J］.Acta Electronica Sinica，2008，36(6):1058-1062.(in Chinese)

［6］ 洪家财，王元钦.底部刻槽旋转弹丸的RCS 特性的分析与仿真［J］.微波学报，2006，22(2):45-48.HONG Jia-cai，WANG Yuan-qin.The RCS analysis and simulation for the bullet pill with slot［J］.Journal of Microwaves，2006，22(2):45-48.(in Chinese)