一种非线性降维改进算法在图像处理中的应用
李德启, 刘传领
(1.商丘职业技术学院计算机系, 河南 商丘 476000; 2.南京理工大学计算机科学与技术学院, 江苏 南京 210094)
0 前 言
图像模式识别技术是信息处理领域的重要分支之一,尤其在侦察、金融和管理等部门具有广阔的应用和发掘前景,它已经成为模式识别和人工智能方面一个重点研究课题.为了更好地完成对图像的识别,对高维图像(如人脸图像)进行降维是对图像识别之前的关键技术环节,因为通过降维处理后的图像计算复杂度有了明显的降低,存储空间也有了明显的节省.目前,对高维图像数据进行降维的方法主要有线性降维(如LDA[1]和PCA[2]等)和非线性降维方法(如LLE[3]和ISOMAP[4]等)两种.线性降维方法虽然能够通过性能目标寻找线性变换矩阵实现对高维数据的降维,但由于光照、表情和姿态等因素会使高维人脸图像具有明显的非线性流形特征[5],但是进行数据降维后会产生原有数据的非线性特征丢失的现象,导致图像数据在进行特征提取后数据失真,从而降低了图像的识别率.非线性降维算法虽然能够使训练样本的流形结构得到保持,但却很难通过对新样本点的分析得到低维上的投影,从分类角度上并不是理想的选择.针对上述两种高维图像数据降维方法存在的缺陷,笔者提出了把LDA和LLE相互融合起来的一种新的图像处理方法(简称LDA & LLE),它既能够解决线性降维方法数据降维后产生的原有数据的非线性特征丢失的缺陷,又能够使非线性降维算法在通过对新样本点的分析得到低维上的投影方面存在的问题得到很好的解决.经过实验表明,用此方法处理过的图像识别率比传统的线性和非线性降维方法都高出很多.
1 LDA算法的实现及其分析
线性判别式分析(LDA)是Belhumeur在1996年引入用于模式识别和人工智能领域的经典算法.为了保证投影后的模式样本在新的子空间具有最佳可分离性,它把高维的模式样本投影到最佳鉴别矢量空间,使模式样本在新的子空间具有最小类内散布矩阵和最大类间距离得到实现,保证了压缩空间和抽取分类信息的效果.在对人脸图像处理的过程中,为了消除识别信息与所压制图像之间的差异,把与类内散布的正交的矢量作为特征脸空间,保证了类内离散度和类间离散度的比值最小,从而避免了光照和表情变化等因素对人脸图像识别的影响.

Ψ=argmaxΨ(ΨTSbΨ*(ΨTSWΨ)-1, Ψ=[Ψ1,Ψ2,…,Ψm],Ψm∈RJ
(1)
式中的Sb表示类间矩阵,可表示为:
式中的SW表示类内矩阵,可表示为:

SbΨm=λmSWΨm,m=1,…,M
(2)
2 局部线性嵌入算法(LLE)的实现及其分析
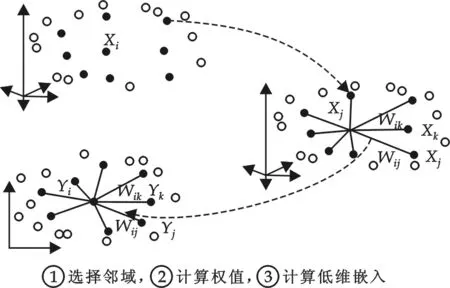
针对LDA算法的缺陷,Roweis和Saul在2000年提出了局部线性嵌入算法(LLE).在LLE算法中高维空间相邻点在低维流形里也是相邻,即它能够很好地保持局部的邻域关系,这也是此方法的一个关键性质.在LLE中,把X={x1,x2,…,xN︱xi∈RD}和Y={y1,y2,…,yN︱yi∈Rd}(d 步骤1:确定在高维空间中样本点的邻域,对每个样本xi(i=1,2,…,N)邻域的确定常用方法有2种:(1)通过某种距离d(.,.)的定义来度量xi到其他样本点的距离,即K邻域的确定,则选取距离最小的K个样本点作为其邻域点;(2)通过ε邻域确定,如果xj落在xi的ε邻域里,则认为xi的一个邻域点是xj. (3) 图1 LLE算法实现步骤示意图 分析步骤2,可以看出在LLE算法中,高维空间中的局部流形来自于高维空间中数据点间的权值.在步骤3中,保持权值不变的条件下得到数据集在低维空间中的局部线性嵌入的新数据集.因此,此种算法可以通过保持数据间的局部联系完成数据从原始高维空间到低维空间的映射.但是,这一步是复杂度相当高,计算最耗时的一步,在没有得到优化的条件下,最小d个特征值的时间复杂度为O(dN2),可以利用对大型稀疏矩阵求解使时间复杂度得到降低.从图1中不难看出,用于重构的权矩阵W是此算法实现的关键,起到了高维数据和低维嵌入之间连接纽带的作用. 虽然利用此算法在高维数据可视化方面取得了较为理想的效果,但还存在着以下几点缺陷: 首先,没有一个显式的方法能够实现新样本点到低维空间的嵌入,并且对新空间维数只能利用验证的方法获得,没有一个显式准则给予确定.其次,此算法不适应对有类标号的样本数据的处理.另外,它虽然在构造的子空间内保持了训练样本的流形结构,但不能够获取新样本点在低维空间上的投影[9],在分类的角度上并不是最理想的算法,尤其对于人脸这类高维非线性流形结构图像的分类问题并不是最优的选择. 基于上述两种数据降维算法的缺陷,笔者在这两种算法分析的基础上,综合各自的优势对它们进行融合提炼,提出了一种新的非线性降维方法(简称LDA&LLE算法).此算法实现的思想可概括为:首先利用线性有监督的LDA算法找到每个样本点的近邻点,然后通过LLE算法中对局部重建权矩阵的计算获取训练集在低维空间中的局部嵌入特征,最后根据高维非线性图像的特点通过对训练集和其低维特征的计算获取新样本的低维特征.这样,此算法通过高维空间和低维空间之间的联系,就能够很好地建立新样本点与其低维特征间明确的映射.该算法的实现过程如下: (1)通过线性判别分析算法(LDA)实现对每个样本点的k个近邻点获取.寻找样本点的近邻点的过程为:首先,通过对训练集x的降维获取LDA子空间A.然后,在高维空间中任意选取两点xi和xj,并且把这两点的距离定义为与其对应的LDA特征点之间的欧式距离,如公式(3).最后,通过新定义的欧式距离完成对每个样本点的k个邻近点的选取. Distanceij=‖ATxi-ATxj‖ (4) (3)根据训练集X及其在上一步骤中获取的低维特征Y, 计算出与新样本对应的低维特征.诸如人脸这类具有明显的高维非线性流性结构的图像,由于它的高维空间和低维空间局部邻域间的点的关系不变,因此只要能够得到新样本点和训练集X之间的邻域关系,就能够计算出新样本点的低维嵌入特征. 假设新样本点为Xnew,首先通过新样本点Xnew向子空间A做投影,从而获得其LDA特征ATXnew,然后通过LLE算法中的公式(3)获取新样本点Xnew的k个近邻点,记作xnewj(j=1,2,…,k),最后利用公式(4)找到新样本点与训练样本间的权值矩阵wnew.对于该新样本点的低维嵌入特征(ynew)的计算,可通过下面的公式完成: (5) 注公式(5)中的ynew表示新样本点在LLE非线性子空间中的低维投影,yi表示获取到的新样本点的近邻点xnewj(j=1,2,…,k) 在LLE非线性子空间中的低维投影. 为了验证笔者提出的算法在非线性降维上的有效性,分别选取ORL和CMU PIE人脸库中的人脸图像进行仿真实验,利用LDA、LLE和LDA & LLE算法进行图像处理和对比实验.在实验前,首先对所用的图像进行自动检测、姿态表情定位和归一化处理,然后利用最近邻分类器进行分类. ORL人脸库由剑桥大学AT & T实验室创建,该数据库包含了具有不同表情和姿势、稍许倾斜(不超过20度)以及不同光照的人脸,共有40个人,每人有10幅不同的人脸图片,共计400张分辨率为92×112的人脸灰度图像[10].本文随机选取每人5幅规一化图像进行训练,其余用作测试,即200幅作为训练样本,其余200幅为测试样本,这样避免了训练集与测试集的交叉现象,如图2所示. 图2 ORL库图像实例 图3 两种算法的仿真实验结果 在实验中,分别选取LLE算法中嵌入空间的维数D=50和每个样本点邻域的个数K=18.使用LDA算法实现降维后,维数不超过其个体类别数减1,并对这些维数逐一进行训练,再用最近邻分类器(NNc)进行分类,将属于不同类的样本均作为代表点,最后通过对这些代表点的比较把测试样本分配至空间距离最小的训练样本所属的类别中.LDA算法与笔者提出的算法在系统中所得到的运行结果如图3所示. 通过此实验可以得出,笔者提出的算法(LDA & LLE)在对图像识别的分类优势方面明显高于线性判别式分析(LDA)算法,并且将图像识别率平均提高了大约4.65%,把对人脸识别系统的识别能力提升到了一个新的高度.此算法综合利用了LDA算法和LLE算法的优势,从而使进行流形降维后一些有利于识别的有用信息的丢失现象得到了避免,达到了降维后的数据依然保持原始特征的目的,使该算法的有效性得到了验证. 表1 CMU PIE库人脸图像实验结果 CMU PIE人脸库是由卡耐基梅隆大学于2000年11月创建,来自于68名志愿者的41 368幅图像,包含了每人13种不同姿态和43种光照条件下的4种表情照片.在此仿真实验中,随机在该库中选取每个人100幅照片,然后再从这100幅图像中随机选取50幅作为训练集,其余的50幅作为测试集,部分实例图片如图4所示.最后,分别用LDA、LLE和笔者提出的LDA & LLE算法对选取的图像进行处理,得出实验结果,如表1所示. 图4 CMU PIE 库图像实例 由表1可以看出,笔者提出的非线性降维算法(LDA & LLE)将图像的识别率提高到了88.21%,明显高于线性判别式分析算法(LDA)和局部线性嵌入算法(LLE),并且在光照、表情和姿态3种因素同时变化的条件下也具有一定的鲁棒性,使系统的识别性能有了显著提高.综合以上两个仿真实验可以得出如下结论: (1)利用LDA算法获取样本近邻点的LDA & LLE算法所获取的低维特征同时具有最小类内差异和最大类间差异的特点,保证了该算法较强的辨别能力. (2)LDA & LLE算法综合了LDA和LLE两种算法进行人脸识别的分类优势,使图像的识别率明显高于其他两种算法. (3)从本质上说,LDA & LLE算法是非线性降维算法,它不但避免了LDA算法中原有数据的非线性特征丢失的现象,而且很好地解决了LLE算法很难通过对新样本点的分析得到低维上的投影的缺陷,即使在光照、表情和姿态等因素同时变化的情况下仍然能够获取识别率较高的图像. 综上所述,笔者提出的非线性降维算法(LDA & LLE)很好地融合了LDA算法和LLE算法的优势,去除了它们中的缺陷,不仅能够使诸如人脸这类高维非线性图像的非线性结构得到了保持,而且具有较强的辨别能力.利用该算法对高维图像的降维效果比较明显,在光照、表情和姿态变化比较大的情况下仍然具有一定的鲁棒性,在提高图像的识别率方面具有广泛的可用性.但对于有关近邻点数目对识别率的影响方面,最邻近点K值的确定是有待解决的问题. 参考文献 [1] P N Belhumeur, J P Hespanha,D J Kriegman. Eigenfaces vs fisherfaces;recognion using class specific linear projection[J].IEEE Trans Pattern Anal.Machine Intell, 2008, 19(7):711-720. [2] Turk M A, Pentland.A P. Eigenfaces for recognition[J].Cognitive Neurosci, 2007, 3(1):71-86. [3] Rowels S T, Saul L K.Nonlinear dimensionality reduction by local linear embedding[J].Science,2000,290(5 500):2 323-2 326. [4] Tenenbaum J B,De Silva V,Langford J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5 500):2 319-2 323. [5] Sam Roweis, Lawrence Saul, Geoff Hiaton. Global coordination of local linear models[J]. Advances in Neural Information Processing System, 2001,14:452-456. [6] Sam T,Rowels,Lawrence K Saul.Nonlinear dimensionality reduction by locally linear embedding[J]. Science,2000,12(290):22. [7] LIU J W,Plaitaniots K N,Venetsanopulos A N.Face recognition using lda based algorithms[J].IEEE Transactions on Neural Networks,2003,14(1):195-200. [8] LIU J W,Plataniotis K N,Vevetsanopoulos A N.Regularization Studies of linear discriminant analysis in small sample size scenarios with application to face reognition[J].Pattern Recognition letter,2005,26(2):181-191. [9] Zhu En, Yin Jianping, Zhang Guomin. Fingerprint Enhance-ment Using Circular Gabor Filter [C]. Proc of Int′l Conf on Image Analysis and Recognition, 2004:750-758. [10] LIAO T W,LI D M,LI Y M. Detection of welding flaws from radiographic images with fuzzy clustering methods[J]. Fuzzy Set and System,1999,108(2):145-158.

3 改进的非线性降维算法的实现
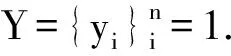
4 仿真实验及结果分析
4.1 ORL人脸库仿真实验及其分析



4.2 CMU PIE人脸库仿真实验及其分析

5 结束语

