GM(1,1)模型的优化及应用
刘 苗, 燕列雅
(西安建筑科技大学理学院, 陕西 西安 710055 )
0 引 言
GM(1,1)模型是灰色系统理论的基础与核心,被广泛应用于工业、农业、社会经济等领域.它将系统看成一个随时间变化而变化的指数函数,不需要大量的时间序列数据就能建立预测模型.近年来,不少学者研究发现了其诸多局限性并做了改进,取得了较好的效果[1-3].文献[4]从背景值的几何意义出发,提出了优化的GM(1,1)模型,从而提高了模型的精度.文献[5]用齐次指数函数拟合一次累加生成序列,由此优化背景值,提高了精度.
本文在文献[4]、[5]对背景值优化的基础上,进一步进行了残差修正,并优化了残差GM(1,1)模型.通过数据比较表明本文优化后的模型预测精度更高,具有较高的应用价值.
1 GM(1,1)模型背景值的优化
1.1 原GM(1,1)模型的建立
设非负的原始序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)},X(0)的一次累加生成序列X(1)={x(1)(1),x(1)(2),…,x(1)(n)},其中
(1)
构造背景值序列Z(1)={z(1)(1),z(1)(2),…,z(1)(n)},其中
z(1)=0.5x(1)(k)+0.5x(1)(k-1)
(2)

则GM(1,1)模型参数的最小二乘估计为
(3)
定义GM(1,1)的白话方程为

(4)

(5)

1.2 背景值的优化


设当Z(1)(k+1)为x(1)(t)在区间[k,k+1]上的背景值时,则有

此处的背景值即为x(1)(t)在区间[k,k+1]上的定积分.
令x(1)(t)=cebt,假设此曲线过点x(1)(k),x(1)(k+1),那么有
x(1)(k)=cebk
(6)
x(1)(k+1)=ceb(k+1)=cebk+eb
(7)
由式(6)、(7)得
优化后的背景值为
(8)
用背景值式(8)替代式(2),再由公式(1)、(3)、(4)、(5)建模并对新的模型进行拟合和预测.
2 残差GM(1,1)模型的优化
z(1)(k+1)为x(1)(t)在区间[k,k+1]上的背景值,当序列为低指数增长序列时,式(5)较适合,模型偏差较小.但当序列为高指数增长序列时,式(5)会产生较大滞后误差,从而导致精度不够高.
现令
(9)
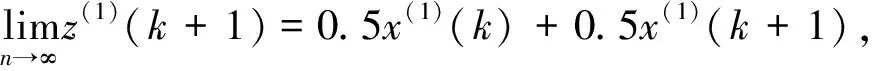

然后建立残差GM(1,1)模型,其残差修正值
优化后的预测值

3 实 例
预测值为
记文献[4]优化的GM(1,1)模型为优化模型1,本文改进的模型为优化模型2,与原GM(1,1)模型的预测值和相对残差作比较,结果见表1.

表1 优化模型与原模型计算结果比较
结果表明,由于原始序列及其残差序列是高指数增长序列,数据变化急剧,因此用原GM(1,1)模型预测结果误差很大,而本文提出的模型精度明显优于文献[4]所给出的模型.
4 结 论
(1) 本文在原模型优化背景值的基础上,进一步对残差模型进行优化,通过实例比较表明其能有效地提高预测精度.
(2) 当残差中有负数时,需先进行非负处理,再建模预测.
参考文献
[1] 刘思峰,党耀国,方志耕. 灰色系统理论及其应用(第三版)[M].北京:科学出版社,2004:125-148.
[2] 刘思峰,党耀国,方志耕,等. 灰色系统理论及其应用(第五版)[M].北京:科学出版社,2010:161-187.
[3]肖新平,宋中民,李 峰. 灰技术基础及其应用[M]. 北京:科学出版社,2005:95-112.
[4] 罗 党,刘思峰,党耀国.灰色模型GM(1,1)优化[J].中国工程科学,2003,5(8):50-53.
[5] 谭冠军. GM(1,1)模型的背景值构造方法和应用(I)[J]. 系统工程理论与实践,2000,20(5):98-103.

