经济预测的神经网络泛化问题研究

冯再勇, 王茂芝

(1.南京铁道职业技术学院基础教学部， 江苏 苏州 215137; 2.成都理工大学数学地质四川省重点实验室, 四川 成都 610059)

0 引 言

利用神经网络建立经济现象的数学模型，据此对经济、金融等问题作出分析、评价和预测，这一方法在经济学理论研究和实证研究中已被广泛采用，也取得了很多有价值的成果.然而在实际利用神经网络进行经济建模、预测时，网络的泛化问题比较突出[1]，造成对某些经济现象的预测和评价不够成功.“泛化问题”即网络泛化性能不够理想的问题，是困扰神经网络应用的最主要问题之一，已成为众多学者十分关注的理论问题.本文从数学与系统科学的角度对利用神经网络进行经济预测时产生泛化问题的本质原因进行了分析，为改善神经网络的泛化性能，更有效的建立经济数学模型提供了有意义的参考.

1 “泛化问题”的数学分析

Kolmogorov定理告诉我们[2]：“对任意连续函数，Ψ:Em→Rn,Y=Ψ(X) ,Em是m维单位立方体:[0,1]m，Ψ可以精确地由一个三层前馈神经网络实现.此神经网络第一层有m个神经元,中间层有(2m+1)个神经元,输出层有n个处理单元”.值得注意的是，由于Y=Ψ(X)是定义在Em=[0,1]m或其子集上的连续函数，因此自变量X(x1,x2,…,xm)的取值有无限多个，相应的可以有无限个Y(y1,y2,…,yn) 与之对应.

建立神经网络模型进行经济预测的本质在于通过神经网络本身的非线性对各种经济系统中隐含的非线性函数、特征进行逼近、提取，最终达到对经济系统进行预测、评价等目的.显然，要保证神经网络预测的信度和效度，最好建立精确实现(至少在一定程度上实现)映射Y=Ψ(X)的三层神经网络.这里，最佳方法就是给出所有X(x1,x2,…,xm)及其象Y(y1,y2,…,yn)的模式对，以此建立精确实现映射Y=Ψ(X) 的三层神经网络.

然而，我们在实际建立神经网络模型时，尽管经济系统内部的非线性特征、函数是确定的，但它却是隐含的、未知的.我们至多能通过统计资料、调查实验手段等得到系统内非线性特征的部分信息——有限个X(x1,x2,…,xm)和Y(y1,y2,…,yn)的对应关系，这有限个模式对便构成了网络建模的基础.

这有限个模式对能不能保证网络模型预测的效度和信度呢？先看在这有限个模式对处，能进行精确插值的不同神经网络有多少个.结合Kolmogorov定理，我们可以得到下面的结论：

结论1在有限个点X1(x11,x12,…,x1m)，X2(x21,x22,…,x2m), …，Xk(xk1,xk2,…,xkm)，(其中：Xi(xi1,xi2,…,xim)∈Em=[0,1]m,i=1,2,…,k)处具有相同映射Y1(y11,y12,…,y1n)，Y2(y21,y22,…,y2n), …，Yk(yk1,yk2,…,ykn)的三层前馈网络有无穷多个，并且有c个. (c即实数集R的“基数”)

证明: 由Kolmogorov定理存在性显然,只需证明满足条件的网络有无穷多个.

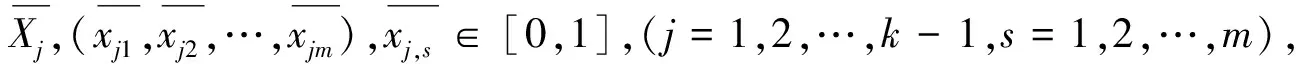
根据实分析中集合间“对等”[3]的概念，对于固定的j有：

进一步对于所有的j有：

其中“∏”是集合的笛卡尔乘积.

这样，就能够得到c组在点:X1(x11,x12,…,x1m)，X2(x21,x22,…,x2m), …，Xk(xk1,xk2,…,xkm)处具有相同映射Y1(y11,y12,…,y1n)，Y2(y21,y22,…,y2n), …，Yk(yk1,yk2,…,ykn)的不同模式对．由Kolmogorov定理，对于每一组给定的模式对都对应一个三层的前馈神经网络可以精确逼近，从而至少存在c个三层网络，在点X1(x11,x12,…,x1m)，X2(x21,x22,…,x2m), …，Xk(xk1,xk2,…,xkm)处有相同的映射：Y1(y11,y12,…,y1n)，Y2(y21,y22,…,y2n), …，Yk(yk1,yk2,…,ykn)．证毕！

另外，Kolmogorov定理成立的前提是连续函数，要求所研究的系统是连续系统.而经济现象中的大量复杂系统都不能确定其连续性，此时Kolmogorov定理就不一定成立，这也是神经网络模型产生泛化问题的本质原因之一.

2 “泛化问题”的系统分析

此外，从系统科学角度来看，利用神经网络作经济预测时，其泛化问题还受到以下因素的影响：

(1) 系统外界噪音的干扰：影响经济系统运行的因素复杂多变，涉及数据都是观测数据，在对样本模式对(X1,Y1), (X2,Y2), …，(Xk,Yk) 进行统计观测时，必然会受到各种外界噪音的干扰，产生误差.实际建模的样本模式对是：(X1+x1,Y1+y1), (X2+x2,Y2+y2), …，(Xk+xk,Yk+yk)，其中(xi,yi)是噪音等带来的偏差.样本模式对的准确性受到影响，自然会反映到构建的网络模型上，由此产生泛化问题.

(2) 系统演化过程中外在随机性的干扰：经济系统在演化过程中有时受到很多外在、偶然随机因素的干扰，从而使系统的发展在一定程度上偏离正常的轨道.此时，系统内部的非线性映射发生了扰动，扰动前数据得到的神经网络显然不能准确地反应扰动后的系统规律，造成“泛化性能”不理想.一个显著的例子就是近几年我国发生的地质、气象灾害明显增多且难以预知，这对于区域的经济发展、金融证券、电力供应、交通运输等各个方面都产生了显著的影响.

(3) 经济系统中内在随机性的影响：系统的非线性程度越高，其内在随机性就越明显，系统对初值的敏感性也越强[4]，经济复杂系统尤其如此，这种系统内在的随机性会对神经网络模型的泛化性能和预测效果产生十分严重的负面影响.假设系统Y=Ψ(X)在没有噪音的理想情况下相应的模式对是：(X1,Y1), (X2,Y2), …，(Xk,Yk)，结合第(1)点，实际统计到的模式对是其近似模式对：(X1+x1,Y1+y1), (X2+x2,Y2+y2), …，(Xk+xk,Yk+yk)，其中(xi,yi)是噪音带来的误差，我们只能将后者作为样本模式对.

在线性系统中，当输入误差ΔX=‖(x1,x2,…，xk)‖很小时，相应的输出误差ΔY=‖(y1,y2,…,yk)‖也很小，将Y′(Y1+y1,Y2+y2,…,Yk+yk)作为Y(Y1,Y2,…,Yk)的近似是合理的.

而经济系统大多是非线性的，尤其是近年兴起的混沌经济学研究表明[5-7]，经济学中存在大量混沌系统，它们对初值极为敏感，系统初始状态的“差之毫厘”就会导致系统演化结果的“谬以千里”[8].此时，尽管ΔX=‖(x1,x2,…,xk)‖很小，而由此产生的ΔY=‖(y1,y2,…,yk)‖却很大，仍然将(Y1+y1,Y2+y2,…,Yk+yk)作为Y(Y1,Y2,…,Yk)的近似便不再合适.

实际上对于混沌经济系统，可以证明下面的结论2成立.

结论2对于混沌经济系统，单纯的前馈神经网络无法保证预测结果的可靠性.

证明: 设经济混沌系统Y=Φ(X)是线性空间X⊂Rm到线性空间Y⊂Rn的映射，从而Y=Φ(X)是从X到Y的泛函.定义线性空间X上的距离d1(X1,X2)=‖X1-X2‖，线性空间Y上的距离d2(Y1,Y2)=‖Y1-Y2‖(距离的具体形式不影响证明)，于是，(X,d1),(Y,d2)都构成距离空间.

为便于分析，假设模型的输入、输出误差可以控制到任意精度，即对于任意小的正数ε，都可以保证：

d1(X,X′)=‖X-X′‖<ε,d2(Y,Y′)=‖Y-Y′‖<ε

(1)

另一方面，由混沌系统对初值的极端敏感性可知，即使d1(X,X′)=‖X-X′‖<ε，由此产生的系统输出偏差却很大.即仍然存在一个很大的正数M，有：

(2)

3 结束语

本文以实分析和混沌理论为工具，对经济系统预测中前馈神经网络泛化问题的本质进行了研究，所得到的结论对神经网络在其他领域的预测及泛化问题同样具有重要的推广意义.

此外，上述研究过程启示我们，将其他非线性工具和神经网络进行深度融合有助于增强神经网络模型本身的非线性能力，改善其泛化性能，提高模型对经济系统预测的科学性和可靠性.例如将混沌理论、小波分析、灰色系统等和神经网络结合起来，构建混沌网络、小波网络、灰色神经网络等可以提高网络的泛化性能，改进预测的效果[9,10].从应用的角度出发，持续和深入地进行这方面的研究有着重要的现实意义.

参考文献

[1] 周志华.神经计算中若干问题的研究[D].南京:南京大学博士学位论文,2000.

[2] Kolmogrov A N. On the representation of continuous function of many variables by superposition of continuous functions of one variable and addition[J]. American Math Society Trans, 1963, 28(1):55-59.

[3] 程其襄，张奠宙，魏国强，等.实变函数与泛函分析基础[M].北京：高等教育出版社，1983.

[4] 孙 霞，吴自勤，黄 畇. 分形原理及其应用[M]. 合肥：中国科学技术大学出版社，2003.

[5] 储海林, 吕小宁, 李 哲.分形与统计学[J].统计研究，2004,(2):35-37.

[6] 张 梅, 萧其尹.论混沌经济的演进与发展[J].商业时代,2005,(14):10-11.

[7] 罗 勇，罗 猛.混沌、复杂性及经济分析[J].统计与决策，2006,(6)：137-140.

[8] 黄润生，黄 浩.混沌及其应用[M].武汉：武汉大学出版社，2000.

[9] 胡俊胜，肖冬荣，夏景明.基于小波神经网络的经济预测研究[J].统计与决策，2005,(6):18-20.

[10] 周志刚，郭 科，陈丽红.时序数据预测的灰色神经网络技术[J].统计与决策，2007,(1):128-129.