平面一般运动刚体上点轨迹曲率半径和曲率中心的分布规律研究及应用

王允地， 王良文， 张航伟

(1．陕西科技大学机电工程学院, 陕西 西安 710021； 2.郑州轻工业学院机电工程学院, 河南 郑州 450002)

0 引 言

机构运动几何学综合是机械学中的一个重要领域.由该方面知识我们知道，作平面一般运动的刚体在每一个瞬时通常存在着一个速度为零的点，称为速度瞬心.在刚体运动过程中，瞬心在静坐标系上绘出的曲线称为静瞬心线，在固连于刚体的动坐标系上绘出的曲线称为动瞬心线.从外界观察，固连于刚体上的动瞬心线绕着固连于机架上的静瞬心线作无滑动的纯滚动.例如，周转轮系中行星轮的节圆绕着固定太阳轮节圆作纯滚动.摆线针轮机构中摆线轮节圆绕固定轮节圆作纯滚动.双滑块机构的动瞬心线是以连杆为直径的圆，静瞬心线则是直径为其两倍的内切圆.反平行四边形机构连杆的动瞬心线及静瞬心线分别是两个形状相同的椭圆.有整转副的双摇杆机构连杆的动瞬心线是具有3个结点且处处外凸的封闭曲线，静瞬心线则是无结点且处处内凹的单封闭曲线.纯滚动约束的引入，使得运动刚体成为以瞬心移动距离S为广义坐标的单自由度系统.给定了刚体的动瞬心线和静瞬心线形状及瞬时接触点位置，刚体的运行过程及点轨迹、轨迹曲率半径和曲率中心便随之确定,而研究某一瞬时动刚体上点轨迹曲率半径和曲率中心的确定方法和分布规律，则对于鹤式起重机构、曲线导引机构、摆线针轮机构、近似等传动比四杆机构等的设计以及四杆机构连杆点轨迹图谱的绘制[14]都具有重要意义.

作者从基本的理论力学知识出发，建立了各种情况下动瞬心线角速度与瞬心移动速度及动、静瞬心线曲率半径之间的关系;利用相对运动原理，得到动刚体上瞬心加速度和拐点圆直径计算式;接着利用微分几何知识，给出了由拐点圆直径和动点极坐标所决定的动刚体上各点轨迹曲率半径的计算通式;阐述了拐点圆直径和动点轨迹曲率中心的3种图解作法.通过研究得出了点轨迹曲率中心的分布规律,描述了动瞬心线法线上点轨迹曲率半径的变化规律.

作者给出的动点轨迹曲率半径计算公式及用辅助圆做动点轨迹曲率中心的图解法,适用于整个动刚体平面，是对经典文献[6,10]和现有文献[5，8]的补充.

以本文所述的理论和方法为基础，在本文的最后给出了一种鹤式起重机构设计方法.

1 角速度与瞬心加速度

给定瞬心P沿瞬心线的移动距离S随时间的变化规律，动、静瞬心线的接触方式及曲率半径，动刚体的纯滚动角速度及与瞬心重合点的加速度便随之确定.以下分4种情况加以讨论.

1.1 静瞬心线为直线而动瞬心线为圆

如图1所示，静瞬心线为直线，动瞬心线为以R为半径的圆.瞬心P沿静瞬心线的绝对运动为变速直线运动，沿动瞬心线的相对运动为变速圆周运动，而动刚体的牵连运动则为动瞬心线绕静瞬心线所做的无滑动纯滚动.由理论力学知识不难看出，动刚体的角速度ω为动瞬心线法线转角对时间t的导数，即

(1)

ap=Dω

(2)

(3)

方向由瞬心P指向圆心O，其值与动刚体的角加速度无关.

图1 静瞬心线为直线而动瞬心线为圆 图2 动、静瞬心线均外凸

1.2 动、静瞬心线均外凸

如图2所示，动、静瞬心线在速度瞬心P处均外凸.静瞬心线的曲率中心为O1，曲率半径为R1；动瞬心线的曲率中心为O2，曲率半径为R2.瞬心P沿静瞬心线作绝对运动，沿动瞬心线作相对运动，而动瞬心线则绕静瞬心线作牵连滚动.动刚体的角速度ω为动瞬心线相对于瞬心线切线的转角与瞬心线切线相对于静瞬心线的转角两者之和对于时间t的导数，即

(4)

(5)

方向由P点指向O2点，其值与动刚体的角加速度无关.

1.3 动瞬心线外凸而静瞬心线内凹

如图3所示，在瞬心P处动瞬心线外凸，而静瞬心线内凹.静瞬心线的曲率中心为O1，曲率半径为R1，动瞬心线的曲率中心为O2，曲率半径为R2.类似地可以得出，动刚体的角速度ω为

(6)

(7)

方向由P点指向O2点，其值与角加速度无关.

图3 动瞬心线外凸而静瞬心线内凹 图4 动瞬心线内凹而静瞬心线外凸

1.4 动瞬心线内凹而静瞬心线外凸

如图4所示，在瞬心P处动瞬心线内凹，而静瞬心线外凸.静瞬心线的曲率中心为O1，曲率半径为R1；动瞬心线的曲率中心为O2，曲率半径为R2.类似地可以得出，动刚体的角速度ω为

(8)

(9)

方向沿瞬心线法线指向动瞬心线所在的一侧，其值与角加速度无关.而动瞬心线为直线则是R2等于无穷大，即1/R2等于0的特例.

2 拐点圆、加速度瞬心及动点轨迹曲率半径计算式

图5 拐点圆与加速度瞬心

2.1 拐点圆与加速度瞬心

定义动刚体上在动瞬心线一侧于瞬心P处与瞬心线切线相切且直径为D的圆为拐点圆，拐点圆与瞬心线法线的交点W为拐极，如图5所示 .

tanβ=ε/ω2

(10)

当动刚体角加速度为零时，加速度瞬心P′与拐极W重合.而当动刚体角速度为零时，加速度瞬心P′则与速度瞬心P重合.

2.2 动点轨迹曲率半径计算式

动、静瞬心线的接触方式和曲率半径给定后，拐点圆便随之确定，动刚体上任一点C轨迹的曲率中心C*及曲率半径ρ也随之确定.

图6 动点C的极坐标及曲率中心

曲率中心C*必然位于动点C与瞬心P的连线，即动点轨迹法线上.以瞬心线法线Px为横轴，瞬心线切线Py为纵轴建立瞬时自然坐标系xPy，Px轴指向动瞬心线所在的一侧.动刚体上任一点C的极径为r，极角为φ，如图6所示.

(11)

如图6所示，由于

(12)

所以

(13)

参看本文作者所写的文献[12]，对上式进行化简，取掉绝对值符号，得到一个扩展公式：

(14)

从中看出，该式为由动点极坐标和拐点圆直径D所决定的计算动点轨迹曲率半径ρ的通式，其计算结果为代数值.动点C位于拐点圆上时，r等于Dcosφ，上式分母为零，曲率半径ρ为无穷大，曲率中心C*处于无穷远.动点C位于拐点圆内时，分母小于零，ρ的计算结果为负， 曲率中心C*处于PC射线上.动点C位于拐点圆外时，分母大于零，ρ的计算结果为正，曲率中心C*处于CP射线或线段上.

3 拐点圆直径和动点轨迹曲率中心的图解法

3.1 拐点圆直径的图解法

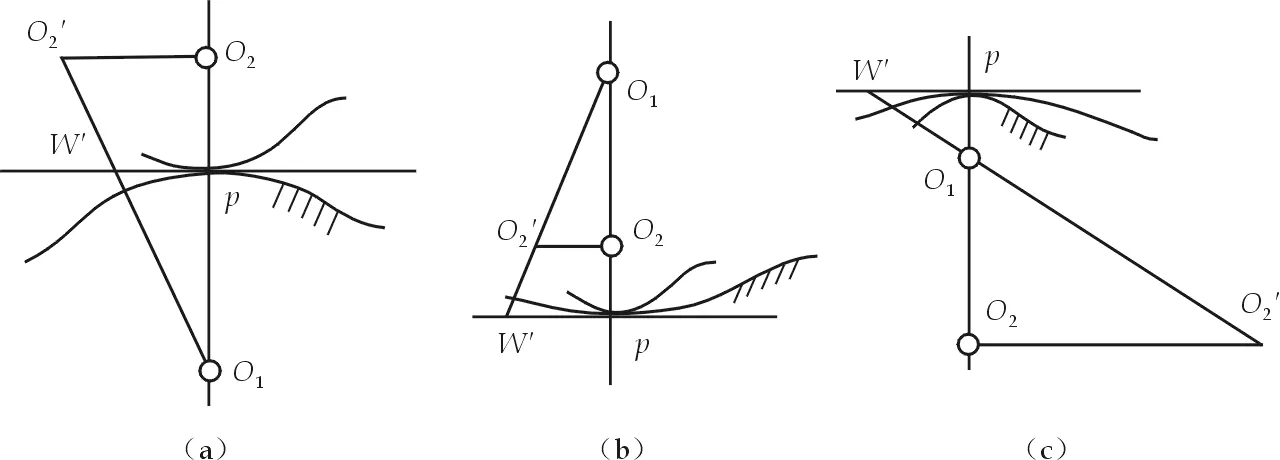
图7 拐点圆直径的图解法

3.2 动点轨迹曲率中心的图解法

3.2.1 利用辅助圆求解

如图8所示，称以PW′为直径的圆为辅助圆.作CC′垂直于PC并取其长度仍为动点C的极径r，再过P作PC的垂线交辅助圆于P′,连P′、C′交PC于C*，即得动点C的曲率中心.设C″为P′在CC′上的投影，利用直角三角形C*CC′与直角三角形P′C″C′的相似性，结合公式(14)，不难证明该作法的正确性.

3.2.2 利用拐点圆求解

如图9所示，过瞬心P作极径PC的垂线与拐极W及动点C的连线交于C′， 再过C′作PW的平行线交PC与C*，即得动点C的曲率中心.设C″为W在PC上的投影，利用直角三角形PCC′与直角三角形WCC″的相似性及直角三角形PC′C*的边角关系，结合公式(14)，也不难证明该作法的正确性.

图4 8 用辅助圆作曲率中心 图9 利用拐点圆求解 图10 用动、静瞬心线曲率中心求解

3.2.3 利用动、静瞬心线的曲率中心作

如图10所示，O1为静瞬心线曲率中心，O2为动瞬心线曲率中心.过瞬心P作极径PC的垂线，交动点C与O2的连线于C′，再作C′与O1的连线交PC于C*，即得动点C的曲率中心. 该图解做法在经典文献[6,10]中已有介绍，故证明过程从略.

4 动点轨迹曲率中心及曲率半径的分布规律

根据用辅助圆作动点轨迹曲率中心的图解法不难看出，各种情况下O2点轨迹的曲率中心均为O1点，而瞬心线切线上各点轨迹的曲率中心均为速度瞬心P点.我们称此为规律一.

对(14)式进行一系列数学运算，利用更比定理及分比定理，我们推得

(15)

参看图6，在x轴的负方向截PW″等于拐点圆直径D，且称以PW″为直径的圆为极限圆.显然，极限圆与拐点圆互为影像.再根据用辅助圆作动点轨迹曲率中心的图解法，可以看出，沿x轴正向从P到W之间依次任取动点C，其曲率中心C*将沿x轴正向从P变到正无穷远处.再沿x轴正向从W到正无穷远处依次任取动点C，其曲率中心C*将沿x轴正向从负无穷远处变到W″处.接着沿x轴正向从负无穷远处到P依次任取动点C，其曲率中心C*将从W″变到P处.结合规律二，可以得出，拐点圆内各动点轨迹的曲率中心分布于动瞬心线所在一侧的整个区域内,拐点圆上各点轨迹的曲率中心均位于无穷远处,动瞬心线所在一侧拐点圆外各动点轨迹的曲率中心分布于静瞬心线所在一侧极限圆外的区域中,静瞬心线所在一侧整个半平面内各动点轨迹曲率中心分布于极限圆内,而动刚体上无穷远处各点轨迹的曲率中心均位于极限圆上,我们称此为规律三. 另外，通过对(14)式的研究，我们得出瞬心线法线上动点轨迹曲率半径的变化规律如下.

图11 由动刚体上两点及对应的曲率中心求拐点圆直径与方位

当动点C在x轴上坐标从零变到1/2D, 其轨迹曲率半径的绝对值平缓地从零上升到1/2D. 坐标从1/2D变到D, 其轨迹曲率半径的绝对值迅速地从1/2D上升到无穷大.坐标从D变到1.5D, 曲率半径迅速地从无穷大下降到4.5D.坐标从1.5D变到2D, 曲率半径平缓地从4.5D下降到4D，并达到极小值.坐标从 2D变到3D, 曲率半径平缓地从4D上升到4.5D.坐标从3D变到无穷大, 曲率半径平缓地从4.5D上升到无穷大. 坐标从负无穷大变到-D, 曲率半径平缓地从无穷大下降到1/2D.坐标从-D变到零, 曲率半径平缓地从1/2D下降到零.

5 鹤式起重机构设计实例

如图11所示，像铰链四杆机构连杆那样，若已知动刚体上两点A、B及其对应的曲率中心A*、B*，那么连架杆AA*及BB*的交点即为连杆AB的速度瞬心P,两动点极径r1、r2及其夹角δ也随之确定.

图12 鹤式起重机构设计

利用计算动点轨迹曲率半径的通式(14)得到两个联立方程

(16)

从中解出PA的极角φ1及拐点圆直径D，动刚体AB在该瞬时的拐点圆形状及方位便唯一确定.由此可见，若取铰链四杆机构的连杆点为拐极W，该点轨迹将是接近于与拐点圆相切的直线.据此可以给出鹤式起重机构的一种设计方法.

如图12所示，为保证鹤式起重机滑轮中心轨迹接近于水平直线，预先给定瞬心线法线Px向下垂直于地面，拐点圆直径D亦根据实际情况任取.再选拐极W为起重臂滑轮中心，适当选取起重臂方位线及两动铰A、B的位置.根据用拐点圆作动点轨迹曲率中心的图解法，求出两动点A、B对应的曲率中心A*、B*作为定铰链，则铰链四杆机构B*BAA*W即为所要设计的鹤式起重机构.

参考文献

[1] 王 铎,程 靳. 理论力学[M].北京：高等教育出版社，2002.

[2] 孙 桓.机械原理[M].北京：高等教育出版社，2001.

[3] 王允地,王良文.并联等效电阻和综合曲率半径的图解分析法及其变化关系[J].陕西科技大学学报，2010，28(5)：138-140.

[4] 祝毓琥. 机械原理[M].北京：人民教育出版社，1979.

[5] 华大年,唐之伟. 机构分析与设计[M].北京：纺织工业出版社，1985.

[6] 阿尔托包列夫期基著,孙可宗译.平面机构综合[M].北京：人民教育出版社，1980.

[7] 彭国勋,肖正杨.自动机械的凸轮机构设计[M].北京：机械工业出版社，1990.

[8] 楼鸿棣,邹慧君.高等机械原理[M].北京：高等教育出版社，1990.

[9] R.L.Norton著，陈立周译.机械设计：机器和机构综合与分析[M].北京：机械工业出版社，2003.

[10] R 贝伊尔著，陈兆雄译.机构运动学综合[M].北京：机械工业出版社，1987.

[11] 王允地,王良文.曲柄摇杆机构和曲柄滑块机构的速比极值条件研究[J].陕西科技大学学报，2007，25(3)：112-114.

[12] 王允地,王良文.用复矢量法建立机械设计中曲线曲率半径和曲率中心的统一计算式[J].陕西科技大学学报，2009，27(2)：108-113.

[13] 叶其孝,沈永欢.实用数学手册[M].北京：科学出版社，2006.

[14] Yang Jihou. The space model and dimensional types of the four bar mechanisms[J]. Mechanism and Machine Theory, 1987,22(1):58-61.