利用改进的正则化方法求解声波散射问题

姚支聪, 王桃正

(西北大学数学系, 陕西 西安 710127)

0 引 言

在均匀介质中，对软介质表面障碍时间调和声波散射问题归结为Helmholtz方程的Dirichlet外问题[1，2],可以利用单层位势理论将问题转化为第一类积分方程，应用正则化方法进行求解[4].本文应用改进的Tikhonov正则化方法求解声波散射问题，并给出了数值例子，结果表明该方法有效，简单，且具有较高的精度.

1 第一类积分方程

考虑在均匀介质中传播的声波，此波碰到一个障碍发生散射，设入射波为ui,散射波为us，我们需要求散射us，此声波碰到一个无穷长的柱体，柱体截面D⊂R2，Γ=∂D，母线平行于Z轴，设入射波是平面波，us=eikx·α,x∈R2,k>0 是波数，α是单位向量，记总体场为u=ui+us,总体场满足Dirchlet边界条件，控制方程为Helmoltz方程.正散射问题是求解u∈C2(⊂R2∩(R2D))满足

(1)

(1)式称为Sommerfeld辐射条件，在所有x/|x|方向一致成立，由Rellich′s和Freholm选择定理[1]，辐射条件保证了问题解的存在唯一性.由:

Δu+k2u=0 inR2

(2)

u=0 on ∂D

(3)

(sφ)(x)=f(x)

(4)

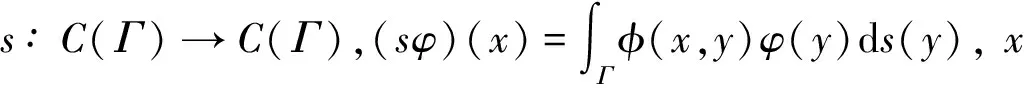
定理1[2]设k2不是D内负Laplace算子的Dirichlet特征值，则算子s∶C(Γ)⊂L2(Γ)→L2(Γ)是单射的且有稠密的值域.

利用Tikhonov正则化方法求解第一类算子(4)就是求解如下极小问题:

其中α>0为正则参数，由文献[2]知，上述极小化问题的解存在并且唯一.

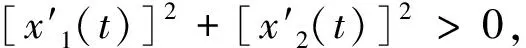
若Γ是解析的,则M1、M2也是解析的，由J0、Y0的级数表示则有:

C=0.577 21表示Euler常数.

2 改进的Tikhonov正则化方法

对于第一类算子方程

kx=y

(5)

求解的问题，其中k∶x→y是线性有界算子，x,y是Hilbert空间，通常情况下，当k为紧算子时，方程(1)的解是不适定的[8,9]，Tikhonov正则化常用的数值方法,但是其正则解的渐进收敛阶不够高[9,10]，研究算子方程的正则化方法就是研究正则化算子的方法，以及相应正则化参数的选取方法，使得正则逼近解收敛于精确解并且具有最好的收敛率.

对于算子方程(5)，考虑定义的迭代的Tikhonov正则化方法:

(6)

当m=1时就是通常的Tikhonov正则化方法，迭代的正则化方法保证了误差估计总可达到阶数最优.本文求解声波散射问题取m=2，对于第一类积分方程(4)，则有

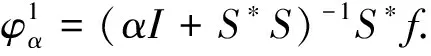
离散(6)式可得到线性方程组

(X*X+αA*A)2μ=(2αA*A+X*X)X*b

(7)

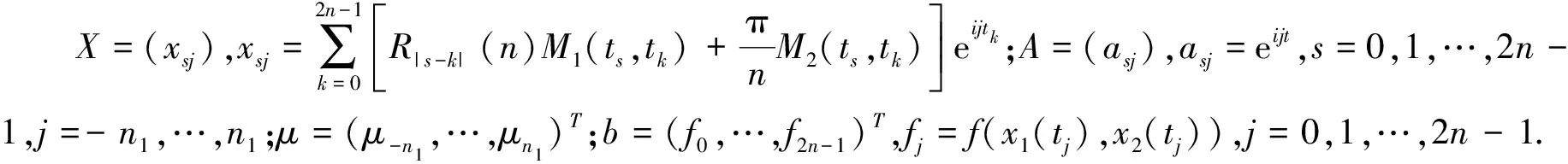
改进的Tikhonov正则化方法，第一类算子方程(4)的正则化求解公式为:

(8)

这里σ=4，则式(8)离散化的线性方程组为

(X*X)2ψ+αIψ=(X*X)2X*b

(9)

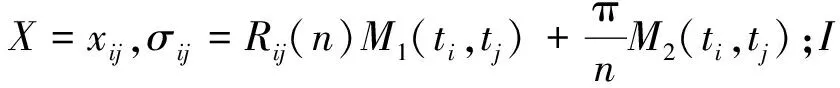
(10)

求解线性方程组(9)得到ψ，带入式(10)得到远场模式.

下面给出数值例子以比较两种方法，设Γ的参数方程表示:

x(t)=(cost+0.65cos2t-0.65,1.5sint),0≤t≤2π

入射方向取d=(0,1),n=64，应用迭代的方法得到的结果如表1、表2所示.

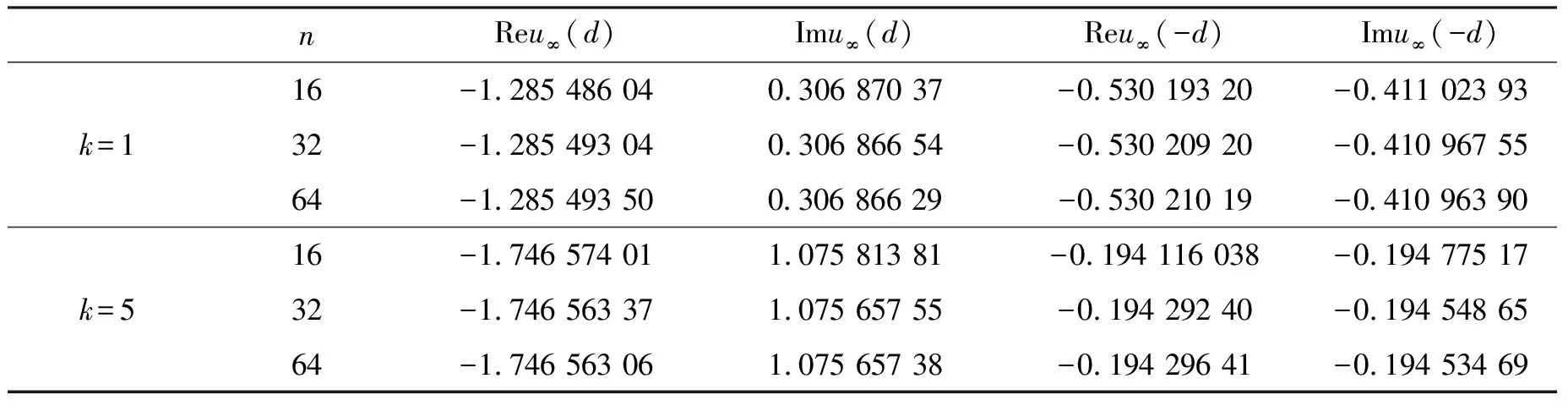
表1 应用迭代Tikhonov的正则化方法求得的远场模式数值解

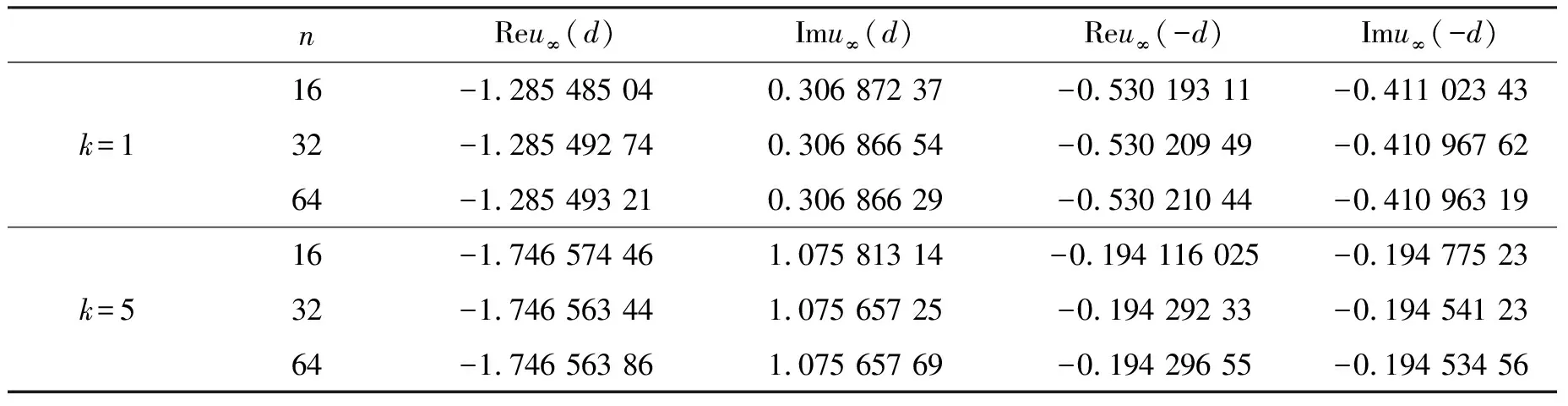
表2 应用改进的Tikhonov的正则化方法求得的远场模式数值解

参考文献

[1] Kress R.Linner IntergralEquation[M].NewYork:Springer-Verlag,1989.

[2] Colton D.Kress R.Inverse Acoustic and Electromagnetic Scattering Theroy[M].NewYork:Springer-Verlag,1992.

[3] ColtonD.Kress R.Integeral Equation Methods in Scattering Theroy[M].New York:WileY-interscience Publication,1983.

[4] 王连堂.用正则化方法求解声波散射问题[J].西北大学学报(自然科学版)，2001，(5):369-371.

[5] 李功胜，马逸尘.应用正则化建立求解不适定问题的正则化方法的探讨[J].数学进展，2000，29(6):531-541.

[6] 傅初黎，李洪芳.不适定问题的迭代Tikhonov正则化方法[J].计算数学，2008，28(3):237-246.

[7] Greotsch C W.The Theory of Tikhonov Regularization for Equation of the First Kind[M].Pitman Advanced Publishing Program,1984.

[8] KirschA.An Introduction to the Mathematical Theory of Problem[M].New York: Applied Mathematical Sciences Springer, 1996.

[9] Engl HW, Hankle M Neubauer.A Regularization of Inverse Problems[M].Dordrecht:Kluwer Academic Publishers，1996.

[10] 李功胜，马逸尘.应用改进的Tikhonov正则化求解Symm积分方程的数值分析[J].工程数学学报，2004，5(21):825-828.