二维单层原子晶格振动的研究
张晓军, 陈长乐, 高 宾,, 王安祥
(1.西安工程大学理学院, 陕西 西安 710048;2.西北工业大学理学院, 陕西 西安 710072)
0 引 言
声子色散关系的研究对固体材料的扩散和相变的了解都非常重要,对固体材料的态密度、晶格摩尔热容、德拜温度以及热膨胀系数等热力学性质的定量研究也是必不可少[1].一直以来,对声子色散关系的研究主要围绕两个方面,即实验测量和理论模拟.由于实验中很难得到单纯的一维原子链,因此对一维原子链色散关系的研究只停留在定性说明而缺少实验依据和理论数据支撑.我们曾针对具体材料,在一维单原子链模型的基础上用数值模拟的方法得到了一维单原子链的色散曲线,弥补了没有具体数据支撑的空缺[2].三维声子色散的研究已趋于成熟.一方面,人们用He原子的非弹性散射(HAS)测量了大量晶体的声子谱并得到了很好的色散曲线[3,4];另一方面把原子势函数和晶格动力学相结合再现了晶体声子色散曲线的实验结果[5].随着实验技术的发展,二维声子谱的实验探测已成为可能,其实验手段主要有电子能量损失谱(EELS)和He原子的非弹性散射(HAS).通过这些方法已得到大量晶体的二维声子谱的实验数据[6, 7],然而缺少理论数据的对比和验证成为了一个问题.本文试探性地建立了体心立方结构金属Ta、W和Mo的二维单层原子的晶格振动模型,在此基础上把两体势和晶格动力学理论相结合,导出了该模型下二维单层原子力常数的表达式和相对应的动力学矩阵,然后用数值计算的方法模拟了沿ГΧ、ГM和ΧM3个高对称方向Ta、W和Mo 3种金属的二维单原子层的色散曲线,为二维声子谱的理论分析和数值模拟奠定了基础,并进一步为二维声子谱的实验结果提供了理论依据.
1 模 型
1.1 二维单原子层的晶格振动模型
Ta、W和Mo均属于体心立方结构,其晶体结构如图1所示,晶格常数为a.在晶体结构中选取(001)晶面作为二维单层原子平面,如图2所示,其中最近邻原子间距为a,原子质量为M.

图1 体心立方晶体结构 图2 二维单层原子
由于热振动,原子会离开它们的平衡位置,以图2线框中间的原子为参考原子n,设该原子离开平衡位置的瞬时位移为u(n),与之相近邻的其它原子的瞬时位移为u(m)(m=1,2,3,…).当第m个原子移动时,原子n就会受到这些原子的作用力,则在简谐近似下,原子n的运动方程为:
(1)
式中α,β=x,y是笛卡尔坐标的分量;Φαβ(n,m)是原子力常数,它表示第m个原子在β方向位移单位距离时施加在n原子α方向上的作用力,它是原子间相互作用势能的二阶导数:
(2)
(1)式的格波解为:
(3)
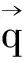
(4)
其中Dαβ(n,m)是动力学矩阵元,具体表达式为
(5)
(4)式是A(n)的2个线性齐次方程,因为晶格振动总是存在的,故A(n)有非零解的条件是:
|Dαβ(n,m)-δαβω2(q)|=0
(6)
只要知道体系的能量,通过求解力常数和动力学矩阵就可以得到体系的振动频率ω(q)和波矢q之间的关系即声子色散关系.
1.2 原子势函数模型
原子势能函数在材料科学、原子动力学、分子振转能级、等离子体等理论的研究方面起着重要作用.早期经常采用的原子势能函数有Morse势和Murrell Sorbie势[8],由于这种模型只考虑了两体相互作用(两体势)因而在应用中受到了限制.与两体势模型不同,多体势模型不仅考虑了两体作用,而且考虑了多体间的相互作用.人们相继提出了多体势模型用于理论模拟或计算,其中较具有代表性的多体势模型有:密度泛函理论(DFT)[9]、嵌入原子势模型(EAM)[5]和ECM方法[10]等.由于二维单层原子间不必考虑多体相互作用,因此我们直接采用张帮为等人所拟合的两体势,其势函数有如下形式[5]:
(7)
其中ks(s=-1~4)是模型参数(见表1),下标e表示平衡状态,r1e表示在平衡状态下纯元素晶体中原子的最近邻距离.把模型参数代入(7)式,可获得Ta、W和Mo的势能曲线,如图3所示.

表1 Ta、W和Mo的模型参数
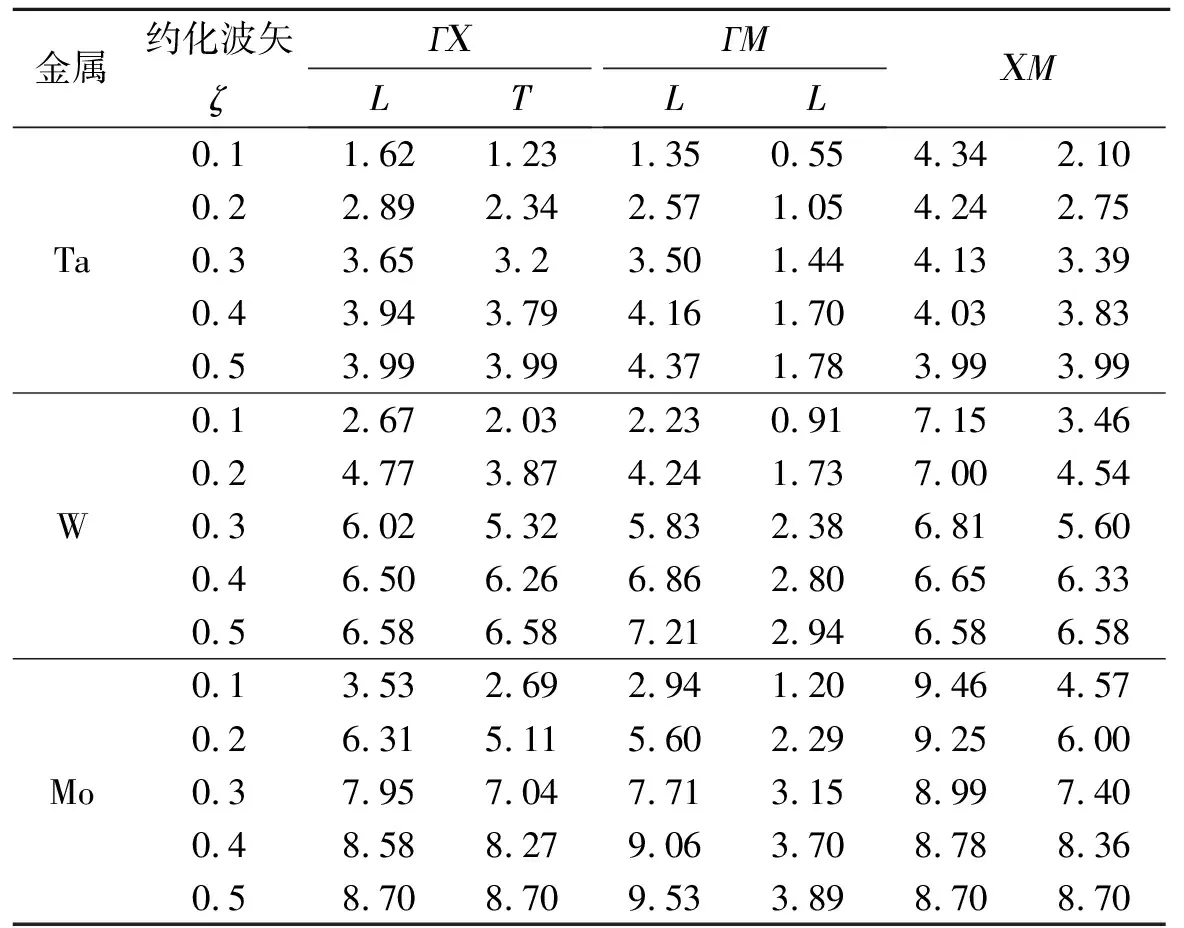
表2 3种金属二维单层原子的振动频率ω(THz)
2 计算和结果
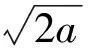
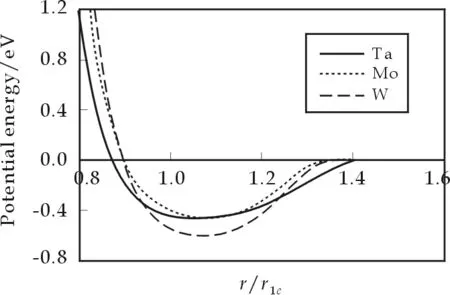
图3 Ta、W和Mo的势能曲线
沿ГΧ、ГM和ΧM3个对称方向即[0ζ]、[1ζ]和[ζζ]方向,Ta、W和Mo 3种金属二维单层原子的声子色散曲线如图4~6所示,其中Γ是二维布里渊区的中心点,M和X是二维布里渊区的边界点,L和T分别表示纵波模和横波模[11].从图中可以看出,Ta、W和Mo 3种金属二维单层原子的声子色散曲线非常相似,只是数值上有些差异.沿ГΧ、ГM和ΧM3个对称方向上,3种金属均有两个独立模,其中在ГΧ和ГM方向上两个独立模分别是纵波模和横波模,而ΧM方向上的两个独立模既不是横波模也不是纵波模.在短波长附近(Γ点)观测到了声子软化现象,即频率和波矢呈线性关系.在M点附近,两个独立模发生简并形成一个独立模.这主要因为在第一布里渊区内,与其它点相比,M点的对称性较高,使两个独立模简并为一个模.如图4~6所示,在相同的对称方向上,3种金属Ta、W和Mo的频率依次增大,这是由于3种金属对应的原子质量(M)依次减小的缘故,因为在相同环境温度下,质量越小的原子状态改变越快,因此频率越大,反之亦然.
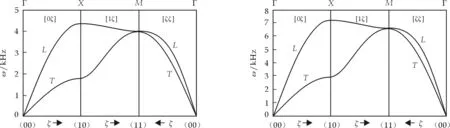
图4 Ta二维单原子层的色散曲线 图5 W二维单原子层的色散曲线
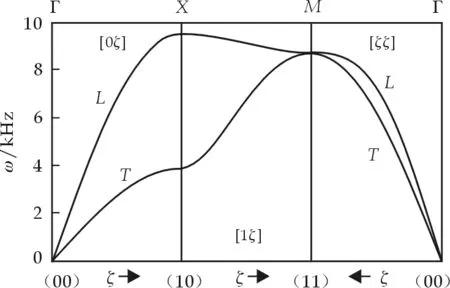
图6 Mo二维单原子层的色散曲线
3 结束语
目前,二维声子谱的实验数据相当丰富,然而缺少理论模型和理论数据的对比,对声子谱的研究也只能停留在实验的基础上,因此建立二维单层原子的晶格振动模型并借助计算机模拟获得色散曲线的第一手数据资料就显得尤为重要.本文构建了体心立方结构金属Ta、W和Mo的二维单层原子的晶格振动模型,在此基础上把运动方程和两体势相结合,在谐和近似下模拟了沿ГΧ、ГM和ΧM3个对称方向Ta、W和Mo 3种金属的二维单层原子的色散曲线,并对这些曲线进行了分析,为二维声子谱的理论分析和数值模拟奠定了基础.该方法也可用于其它晶体结构的二维单层原子色散关系的模拟计算,如面心立方晶体结构.
参考文献
[1] Stassis C, Arch D and McMasters O D. Lattice dynamics of hcp Hf[J]. Phys. Rev. B, 1981, 24: 730-740.
[2] 张晓军,高 宾,王安祥. 一维单原子链晶格振动的定量研究[J]. 宝鸡文理学院学报,2010,30(1):57-60.
[3] Lynn J W, Smith H G and Nicklw R M. Lattice dynamics of gold[J]. Phy. Rev. B, 1973, 8: 3 493-3 499.
[4] Dutton D H, Brockhouse B N and Miller A P. Normal vibrations in platinum[J]. Canadaian Journal of Physics, 1972, 50: 2 915-2 920.
[5] Zhang X J, Zhang J M and Xu K W. Calculation of phonon spectrum for noble metals by modified analytic embedded atom method[J].Chin. phys., 2006, 15(9): 2 108-2 113.
[6] Nelson J S, Daw M S. Cu(111) and Ag(111) surface phonon spectrum[J] . Phys. Rev. B, 1989, 40(3): 1 465-1 479.
[7] Kroger J, Lehwald S. Surface dynamics of Mo(110)-H and Mo(110)-Li[J]. Surf. Sci., 2003, 530: 170-174.
[8] Murrell J N, Sorbie K S. New analytic form for potential energy curves of stable diatomic states[J]. J. Chem. Soc. Faraday Trans., 1974, 70(2): 1 552.
[9] Hohenberg P, Kohn W. In homogeneous electron gas[J]. Phys Rev B, 1964, 136: 864-871.
[10] Liu G Y, Sun W G. Studies on the potential curves of some ex cited states of nitrogen molecule N2using energy consistent method[J]. Chin. J. Atom. Mole. Phys. 2004, 21(2): 255-259.
[11] Allen R E, Alldrdge G P. Studies of vibrational surface modes[J]. Phys. Rev. B, 1971, 4(6): 1 648-1 660.

