基于主元分析神经网络补偿的 感应电动机逆解耦控制

巫庆辉 伦淑娴 常晓恒 尹作友

（渤海大学信息科学与工程学院 锦州 121003）

1 引言

随着微电子技术和电力电子技术的高速发展，交流调速已广泛应用于可变速驱动系统，并具有取代直流调速的趋势[1]。近年来，异步电动机的各种解耦控制方法得到广泛的研究，如基于转子磁链定向的矢量控制、基于定子磁链定向的直接转矩控制、基于微分几何的解耦控制理论、基于非线性自抗扰控制器解耦控制[2]等。矢量控制的解耦思想在保证转子磁链幅值为常数的情况下，将感应电动机解耦成独立的转子磁链回路与转矩回路，仅实现静态解耦而无法实现动态解耦[3]，同时还具有如下的局限性：①转子磁链定向困难；②复杂坐标变换；③对参数变化敏感；④以电流作控制量，适合于电流源型逆变器供电系统，对于电压源型逆变器供电系统，需要电流控制环节。直接转矩控制的解耦思想是依据定子磁链空间位置信息综合定子磁链、电磁转矩的滞环比较器逻辑信号来直接选择逆变器的开关状态。直接转矩控制结构简单、快速性好、鲁棒性强等优点，然而又带来转矩与磁链脉动大、电流畸变、无法结合先进控制理论等问题[4-5]。

基于逆系统的解耦控制方法是利用非线性状态反馈来实现多变量、非线性、强耦合系统的解耦与线性化的，具有直观、简便和易于理解等特点。目前，在转子磁链与电磁转矩、转子磁链与转速、定子磁链与电磁转矩之间的动态解耦方面，基于逆系统的解耦控制方法得到了深入的研究与应 用[6-12]。然而电动机在重载条件下运行时，由于绕组的温升及电流频率引起的集肤效应，定转子电阻的变化量可以达到初始值的50%[13]。电动机定子、转子电阻参数变化给逆系统方法的解析实现带来困难[14]。

本文首先分析与建立了感应电动机的α 阶积分逆模型，在分析非线性状态反馈的误差对其逆模型精度的影响基础上，提出了一个基于主元分析神经网络补偿的感应电动机逆解耦控制方法，将补偿后的α 阶积分逆模型级联到对象的输入端使复杂的感应电动机调速系统解耦成两个独立回路，然后利用线性系统理论分别对独立回路进行综合设计，最后实验验证了该方案的有效性。

2 感应电动机的逆模型

以定子电流矢量与定子磁链矢量的d、q 轴分量及转速为状态变量，即x=(isdisqysdysqωr)T；以定子电压矢量d、q 轴分量为输入变量，即u=(usdusq)T；以电磁转矩与定子磁链模为输出变量，即y=(T φ)T；则感应电动机在静止坐标系下的状态方程为[15]

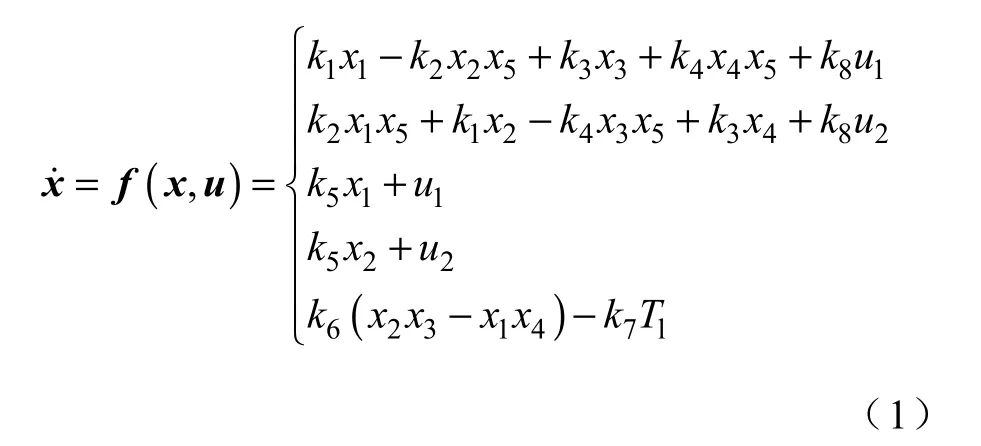
系统的输出方程

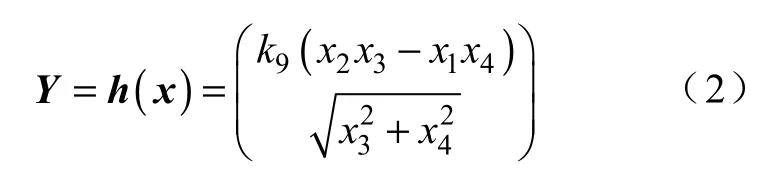
式中，k1=−(Rs+RrLs/Lr)/(σLs)，k2=np，k3=Rr/(σLsLr)，k4=np/(σLs)，k5=−Rs，k6=1.5np/J，k7=1/J，k8=1/(σLs)，k9=1.5np

由系统的输出方程（2）可知，输出量与控制量之间不是显示关系，但是借助状态方程（1）具有隐含关系。为了得到输出量与控制量的显示关系，各输出量分别对时间求导，直到得到输出量与控制量之间的显示关系为止，即[16]

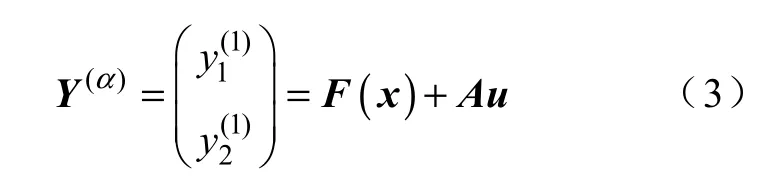
式中

系统的相对阶(α1α2)=(1 1)，且相对阶的总和小于该系统的阶次，同时在正则点的某临域内满足

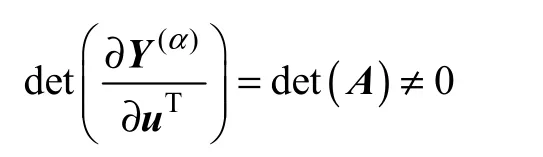
由逆系统存在定理[14]可判断感应电动机调速系统是可逆的。当矩阵A 非奇异时，由式（4）解得控制量的唯一解为

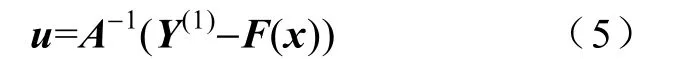
3 α-阶积分逆模型补偿方法

在不考虑状态变量的观测误差情况下，由式（6）可知，逆模型的精度由非线性状态反馈函数F 决定。感应电动机从起动到稳态运行，温升、集肤效应使得定子电阻、转子电阻参数值变化较大，甚至达到其标称值的两倍左右。解析表达式的状态反馈函数过分依赖于电动机参数，实际应用中实现相当困难。神经网络具有：任意精度逼近任意复杂的静态非线性函数；学习并适应未知或不确定的系统；采用并行处理方法，使得快速进行大量运算成为可能；所有定量或定性的信息均匀地分布存储于网络内的各神经元，有强鲁棒性和容错性等优点。本文将非线性状态反馈的解析方法与具有对未知非线性系统逼近能力的神经网络方法结合，构造适合工程应用的基于神经网络补偿的逆模型，具有如下形式：

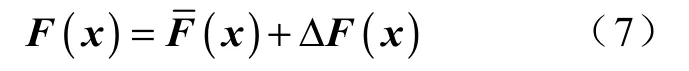
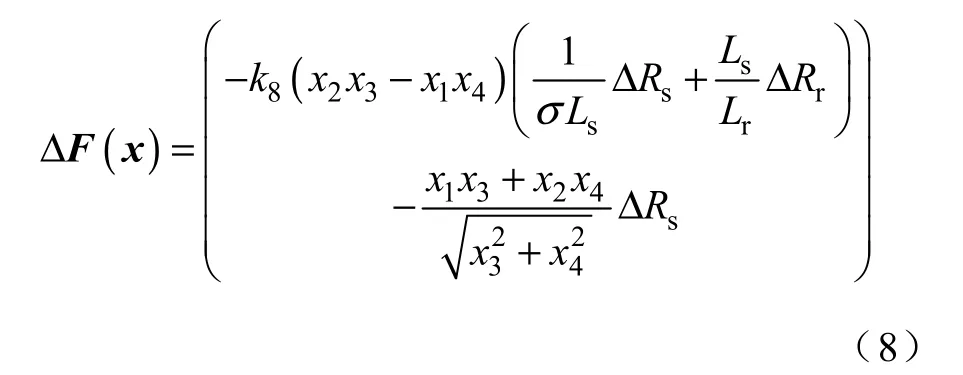
4 基于神经网络逆复合控制器的设计

基于神经网络补偿的逆系统与被控对象复合成一个伪线性子系统。为了获得优良的静、动态特性与抗干扰能力，在此基础上，设计了复合控制器，如图1 所示，包括基于神经网络补偿的解耦控制器与附加PID 控制器两部分。

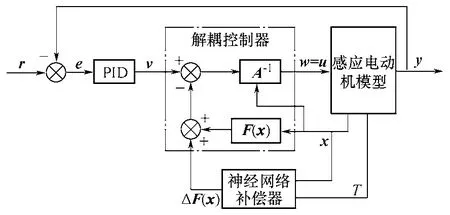
图1 复合控制系统框图 Fig.1 Block diagram of compound control system

4.1 神经网络补偿器[17]

由于定、转子参数是绕组温升的函数，由式（8）可知，逆解耦的补偿量是一个关于系统状态及绕组温度的多变量、强耦合与非线性映射关系，同时又受运行工况等复杂因素的影响。BP 神经网络具有自学习、自适应和较强的容错性，非常适合于该研究的问题，因此，设计了基于BP 神经网络的逆解耦补偿器。又由于输入变量较多、训练样本很大，这样造成神经网络训练时间相当长，效率低，泛化能力差。而主元分析法（PCA）对网络的输入进行线性组合，降低输入量维数，正好解决这个问题。

4.1.1 主元分析法

主元分析法的基本思路是：通过线性坐标变换，用较少的互不相关的变量代替原变量，同时保留原始数据的特征信息。PCA 实质上是过程操作变量协方差的特征矢量分解，其主要思想如下：

设标准化的数据样本集X=(x1x2…xn)T，其协方差矩阵为∑，λ1≥λ2≥…≥λn≥0 为∑的n 个非负特征根，与λi对应的单位特征矢量为 Ai=(ai1ai2… ain)T，i=1,…,n。由n 个特征矢量组成的新变量如下：

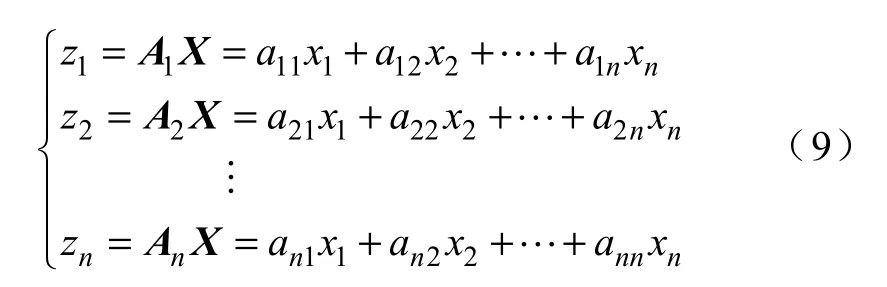
选择前m 个变量为z1，z2，…，zm（m＜n）作为主元分量，使其方差占总方差的比例为（约0.85～

0.9 ）

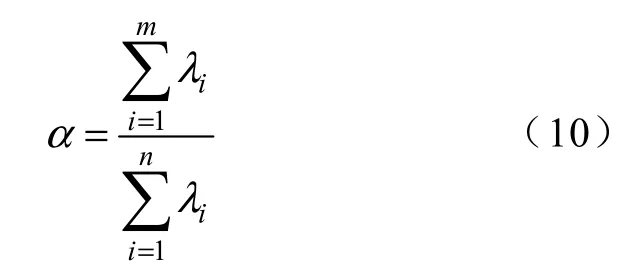
4.1.2 基于PCA 的BP 神经网络结构

数据样本有6 个输入变量与两个输出变量，其中输入变量分别为定子电流矢量的d 轴分量与q 轴分量、定子磁链的d 轴分量与q 轴分量、转速以及电机温度；输出变量分别为两个补偿分量。首先利用Matlab 中的prestd 函数将数据标准化，然后利用主元分析函数prepca 通过指定的占总方差的最小比例将数据样本转化成由四个无关的新变量组成。BP神经网络模型采用4-60-2 结构，基于PCA 的BP 神经网络结构如图2 所示。

4.1.3 样本训练与验证

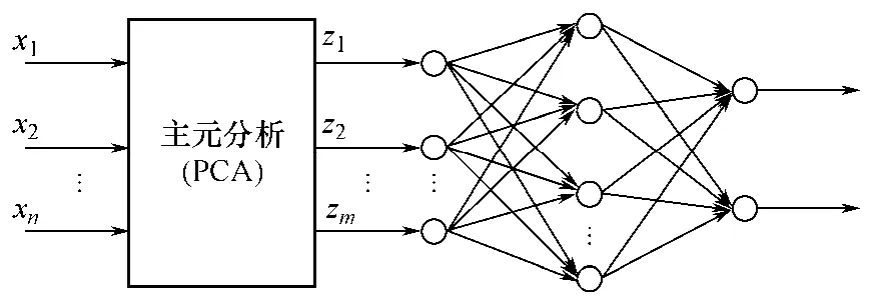
图2 基于PCA 的神经网络结构模型 Fig.2 Structural model of PCA based neutral network

数据样本集共有2000 组数据，其中1500 组数据用于训练神经网络，其余500 组数据用于验证神经网络。本神经网络的训练参数为：终止误差为0， 最大训练步数为20，隐层与输出层的作用函数分别为“tansig”与“purelin”。基于PCA 的神经网络经过 20 次的训练步数时，网络的误差精度达到1.5×10−5。把训练数据之外的500 组验证数据输入到已训练好的神经网络，得到如图3 所示的结果。

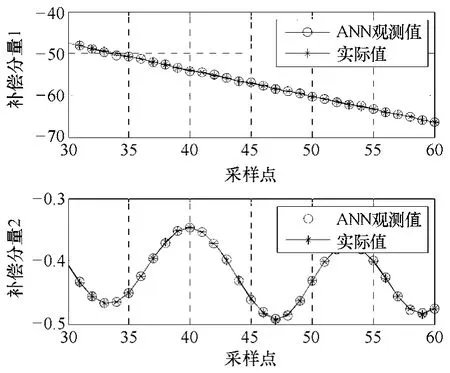
图3 BP 神经网络输出与实际输出曲线 Fig.3 Curves of real output and PCA neutral network output

仿真结果可以看出，网络经过训练学习后，实际输出与模型输出基本相符，能够对逆解耦进行精确补偿。

4.2 PID 调节器

由于转矩子系统与磁链子系统均为一阶积分型线性系统，TA 和FA 均选为PI 调节器，其传递函数分别为

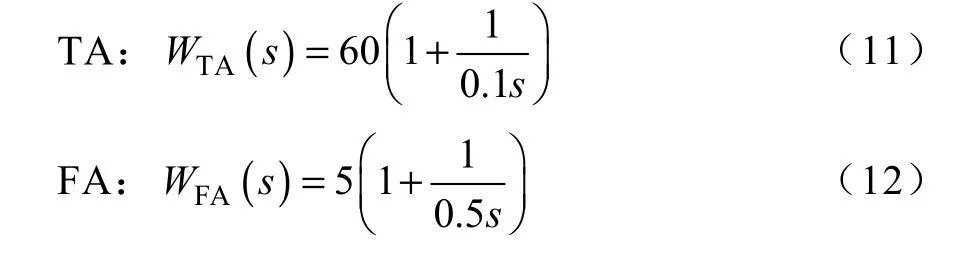
5 仿真与实验研究

按照图1 所示的控制结构对一个标准4kW、4-极的笼型感应电动机进行了实验对比研究。电动机参数如下：Rs=1.1Ω，Rr=1.05Ω，Ls=0.12H，Lr=0.12H，Lm=0.115H。

5.1 未补偿的解耦控制系统仿真结果

5.1.1 验证电磁转矩对定子磁链的动态耦合影响

电磁转矩与定子磁链幅值在初始时刻分别设定为10N·m 和0.4Wb，在3s 时刻电磁转矩给定值突变为20N·m，而定子磁链给定值保持不变，逆系统未采用补偿（也就是图1 中的ΔF(x)=0），电磁转矩与定子磁链响应曲线如图4 所示。

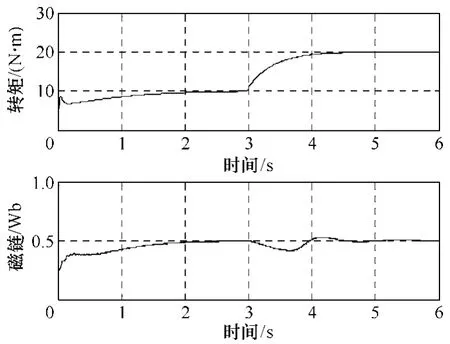
图4 电磁转矩对定子磁链的耦合影响 Fig.4 Coupling influence of electromagnetic torque versus stator flux linkage

5.1.2 验证定子磁链对电磁转矩的动态耦合影响

电磁转矩与定子磁链幅值在初始时刻分别设定为10N·m 和0.5Wb，在3s 时刻定子磁链幅值给定值突变为1Wb，而电磁转矩给定值保持不变，逆系统未采用补偿（也就是图1 中的ΔF(x)=0），电磁转矩与定子磁链响应曲线如图5 所示。

图5 定子磁链对电磁转矩的耦合影响 Fig.5 Coupling influence of stator flux linkage versus electromagnetic torque

5.2 基于神经网络补偿的解耦控制系统仿真结果

逆解耦控制系统采用建议的基于PCA-BP 神经网络补偿方案，并设定电动机的温度与时间的函数关系及定、转子电阻随温度变化关系为

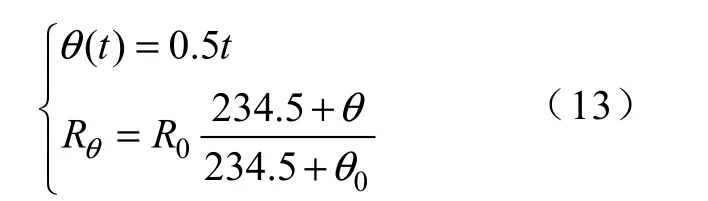
电磁转矩与定子磁链响应曲线如图6、图7 所示，从仿真实验结果可以看出，定转子电阻随温升变化时，基于PCA-BP 神经网络的补偿器得到了精确补偿，实现了定子磁链与电磁转矩完全解耦。

图6 基于补偿方案的电磁转矩对定子磁链耦合影响 Fig.6 Coupling influence of electromagnetic torque versus stator flux linkage based on the proposed scheme

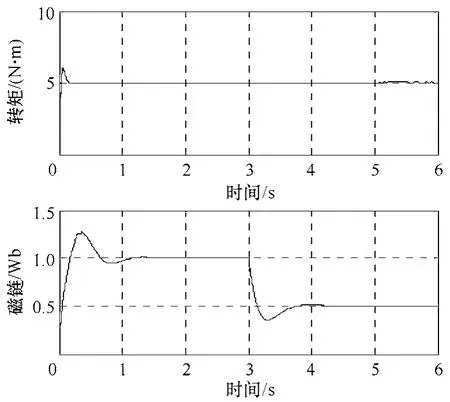
图7 基于补偿方案的定子磁链对电磁转矩耦合影响 Fig.7 Coupling influence of stator flux linkage versus electromagnetic torque based on the proposed scheme

5.3 基于神经网络补偿的解耦控制系统实验结果

本文提出的基于神经网络补偿的解耦控制在EL-DSPMCK-Ⅱ型DSP 电机控制实验开发平台上进行了实验验证。初始时刻，电磁转矩与电子磁链的给定值分别设定为2N·m、0.5Wb，电机空载起动，待平稳运行3s 后，电磁转矩给定值突变为5N·m，运行6s 后定子磁链给定值突变为1Wb，实验结果如图8 所示。从实验结果可以看出，所提方案实现了定子磁链与电磁转矩的解耦控制。

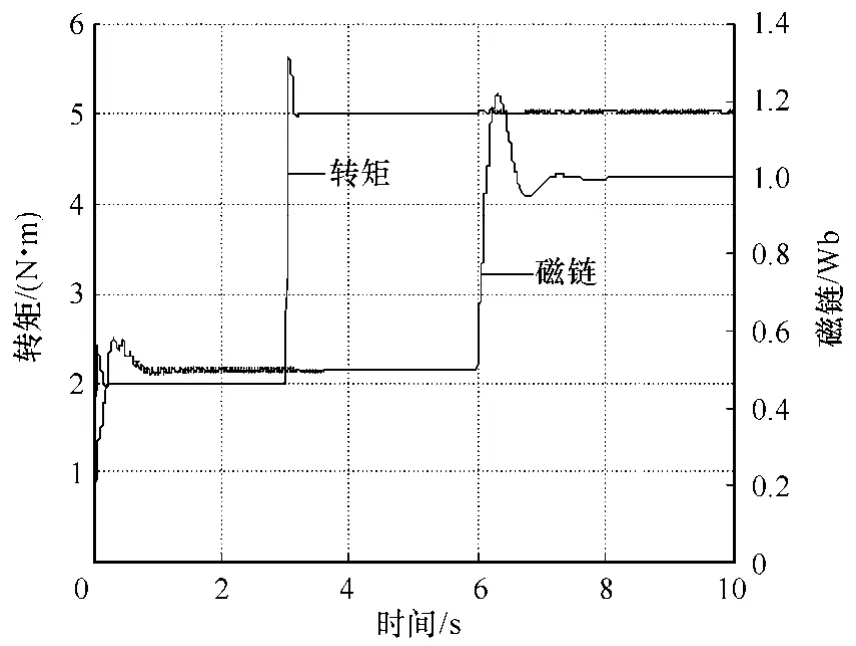
图8 基于神经网络补偿的解耦控制实验曲线 Fig.8 Experimental curves of PCA neutral network compensation based decoupling control

6 结论

本文针对感应电动机驱动系统提出了基于主元分析神经网络逆解耦控制的方法，通过理论分析与实验验证得到如下结论：

（1）定转子电阻参数的变化所造成的非线性状态反馈误差是影响逆解耦控制精度的主要因素，尤其电磁转矩对定子磁链的耦合作用强。

（2）神经网络具有自适应、自学习、较强鲁棒性和非线性映射能力，适合于感应电动机非线性状态反馈误差的补偿。

（3）主元分析法对神经网络输入数据样本进行预处理，大大降低了神经网络输入维数，大大简化了神经网络结构，提高了神经网络收敛速度与泛化能力。

（4）主元分析法得到的新变量为原变量的加权平均，具有滤波作用，可以大大提高系统的抗干扰能力。

[1] 陈硕,辻峰男,山田英二.感应电机无速度传感器矢量控制系统的定子电阻在线辨识[J].中国电机工程学报,2003,23(2):88-92.

Chen S,Tsujt M,Yamada E.On-line identification of stator resistance for sensorless vector control system of induction motors[J].Proceedings of the CSEE,2003,23(2):88-92.

[2] 冯光,黄立培,朱东起.采用自抗扰控制器的高性能异步电动机调速系统[J].中国电机工程学报,2001,21(10):55-58.

Feng Guang,Huang Lipei,Zhu Dongqi.High performance control of induction motor based on auto-disturbance rejection controller[J].Proceedings of the CSEE,2001,21(10):55-58.

[3] 孙飞月,张春龙.异步电动机两种不同解耦控制策略的比较[J].微特电机,2006(11):27-32.

Sun Feiyue,Zhang Chuanlong.Comparative study of two decoupling control methods of induction motor[J].Small & Special Electrical Machines,2006(11):27-32.

[4] 胡虎,李永东.基于区域电压矢量表的交流异步电动机直接转矩预测控制策略研究[J].电工技术学报,2004,19(2):25-30,46.

Hu Hu,Li Yongdong.A predictive direct torque control strategies of induction motor based on area voltage vector table[J].Transactions of China Electrotechnical Society,2004,19(2):25-30,46.

[5] 程善美,付中奇.基于自适应转速辨识的直接转矩控制系统研究[J].电力电子技术,2007,41(9):24-25.

Cheng Shanmei,Fu Zhongqi.Research of direct torque control system based on adaptive speed identi- fication[J].Power Electronics,2007,41(9):24-25.

[6] Kawabata Y,Kawakami T,Sasakura Y,et al.New design method of decoupling control system for vector controlled induction motor[J].IEEE Trans- actions on Power Electronics,2004,19(S):1-9.

[7] 孙东升.基于线性化反馈的异步电动机自适应解耦控制[J].电机与控制应用,2006,33(3):7-11.

Sun Dongsheng.Self-adaptive decoupling control for induction motor based on linearization feedback[J].Electric Machines & Control Application,2006,33(3):7-11.

[8] 曹建荣,虞烈,魏泽国,等.基于逆系统理论的感应电动机解耦控制的研究[J].电工技术学报,1999,14(1):7-11.

Cao Jianrong,Yu Lie,Wei Zeguo,et al.Inverse system-based decoupling control of induction motor[J].Transactions of China Electrotechnical Society,1999,14(1):7-11.

[9] Boton C,Horga V,Albu M,et al.Decoupling control of an induction motor drive supplied by a voltage source inverter[C].International Symposium on Signals,Circuits and Systems,2007,2:1-4.

[10] Wang H,Xu W,Shen T,et al.Stator flux and torque decoupling control for induction motors with resistance adaptation[J].IEE Proceedings on Control Theory and Applications,2005,152(4):363-370.

[11] 李擎,杨立永,李正熙,等.异步电动机定子磁链与电磁转矩的逆系统解耦控制方法[J].中国电机工程学报,2006,26(6):146-150.

Li Qing,Yang Liyong,Li Zhengxi,et al.Stator flux and torque decoupling control of induction motor using inverse system method[J].Proceedings of the CSEE,2006,26(6):146-150.

[12] 杨立永,李正熙,李华德,等.感应电动机调速系统的自适应逆控制[J].控制理论与应用,2007,24(1):95-98.

Yang Liyong,Li Zhengxi,Li Huade,et al.Adaptive inverse control of induction motor drive system[J].Control Theory & Applications,2007,24(1):95-98.

[13] Marino R,Peresada S,Tomer P.On-line stator and rotor resistance estimation for induction motors [C].IEEE Trans.on Contr.Syst.Technol.,2000,8:570-579.

[14] 戴先中.多变量非线性系统的神经网络逆控制方 法[M].北京:科学出版社,2005.

[15] 巫庆辉.感应电动机定子磁链与转矩的逆解耦及存在性[J].控制理论与应用,2009,26(9):983- 987.

Wu Qinghui.The inverse decoupling control for the stator flux and torque in induction motors and its existence[J].Control Theory & Applications,2009,26(9):983-987.

[16] 巫庆辉,伦淑娴.基于定转子电阻误差补偿的感应电动机自适应逆解耦控制研究[J].自动化学报,2010,36(2):297-303.

Wu Qinghui,Lun Shuxian.Research on adaptive inverse decoupling control of induction motor based on stator and rotor resistance error compensation[J].Acta Automatica Sinica,2010,36(2):297-303.

[17] Wu Qinghui,Chang Xiaoheng,Lun Shuxian,et al.PCA-BP neutral network design for inverse decoupling compensator of induction motor drives[C].2010CCDC,Xuzhou,China,2010.