水中有限长功能梯度材料圆柱壳声辐射研究
徐步青, 杨绍普, 齐月芹
(1.石家庄铁道大学 工程力学系,河北 石家庄 050043;2.河北省交通安全与控制重点实验室,河北 石家庄 050043)
0 引言
功能梯度材料( Functionally Graded Material,简称FGM) 是由一种全新的设计概念而开发的新型功能材料。以计算机辅助材料设计为基础,采用先进的材料复合技术,使构成材料的要素( 组成、结构等) 在几何空间上呈连续变化,使材料的性质和功能也呈梯度变化,从而满足构件不同部位对材料使用性能的不同要求。同时,由于该材料对结构中各组分相呈连续变化,不存在明显的界面及性能的突变,具有明显优于一般层叠型复合材料的特性。这种将性能各异的材料按照设计意愿在结构内部非均匀、连续地合成的新型材料将复合材料的研究带入了材料设计的更高层次。
功能梯度材料是在20 世纪80 年代末90 年代初由日本学者新野正之、平井敏雄和渡边龙三等提出的[1],主要用于国防高新技术领域对材料性能提出的特殊要求方面,后来这一概念逐渐被应用于其它功能材料的构思与研究中。目前,该材料在军事、航天、能源、电子、光学、化学和生物医学工程等重要领域得到广泛应用与发展。而圆柱壳结构在这些工程领域得到广泛使用,其声辐射的研究是非常有必要的。
近年来,功能梯度材料及其结构的研究已引起国际学术界广泛关注。目前,对功能梯度材料主要集中在热应力分析、断裂力学行为以及材料优化等方面[2-3],而在声辐射方面的研究鲜有报道。
文献[4]根据均质材料圆柱壳基本理论,将功能梯度材料圆柱壳原始三维变系数控制方程转化为特殊类型各向异性及薄膜-弯曲耦联的二维常系数方程,得到功能梯度材料圆柱壳的基本动力方程。本文在该方程的基础上,利用流体和圆柱壳分界面上振速连续边界条件,推导出了圆柱壳在径向集中力激励下圆柱壳振动平均振速、声辐射效率表达式。本文为研究水下功能梯度圆柱壳结构振动声辐射问题提供了一种有效的分析方法。
1 有限长功能梯度材料圆柱壳体基本解
1.1 基本动力方程
设一半径为a,厚度为h,长为2L 的功能梯度材料有限长圆柱壳,以圆柱壳轴线为z 轴建立如图1 所示柱面坐标系。分别用u,v,w 表示圆柱壳中面上点( a,φ,z) 在轴向z,周向φ 和径向r 的位移。当浸没在重流体中的功能梯度材料圆柱壳受力激励时,其振动方程可表示为[4-5]
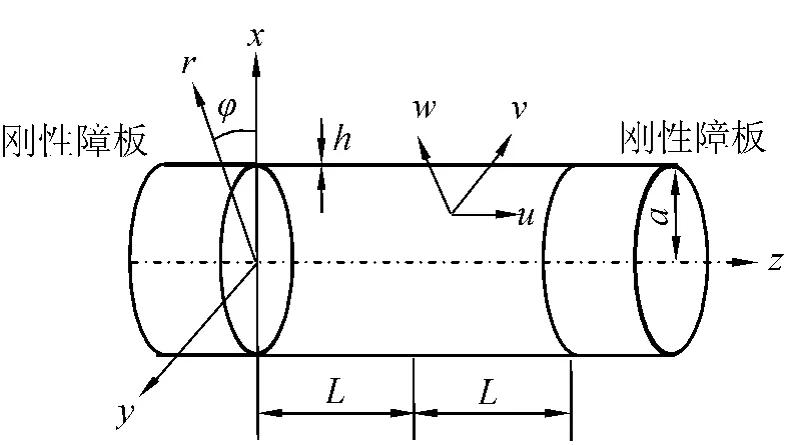
图1 有限长功能梯度材料圆柱壳
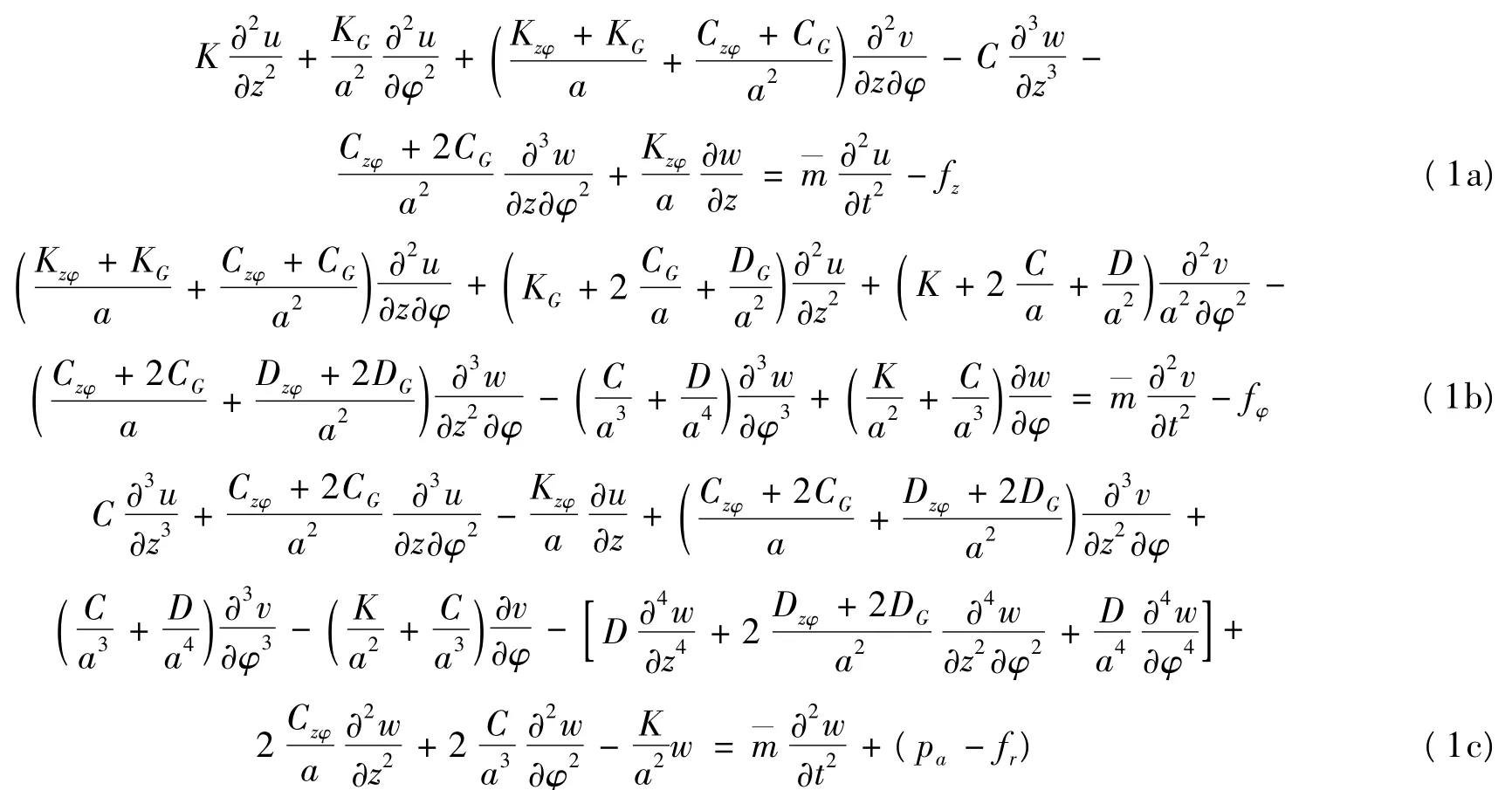
其中薄膜刚度为
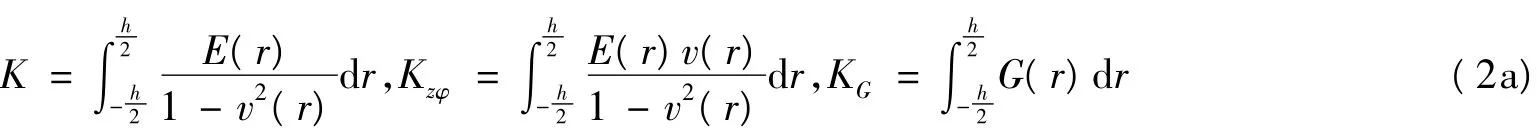
弯曲刚度为
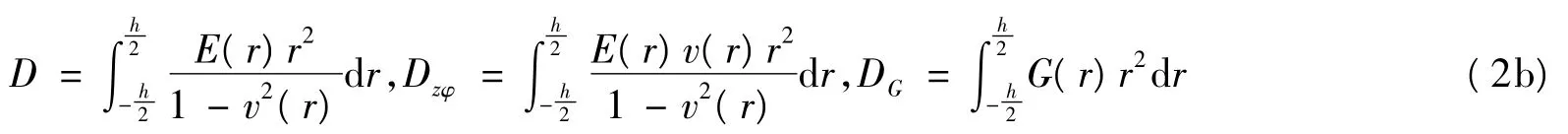
膜弯耦合刚度为
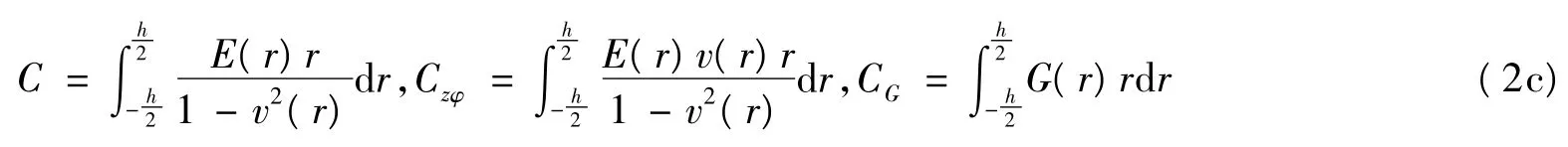
面质量密度为

而ρ、E、G、v 分别为功能梯度材料圆柱壳的密度、杨氏弹性模量、剪切弹性模量和泊松比。
1.2 有限长功能梯度圆柱壳的振动与声辐射
当有限长功能梯度材料圆柱壳置于声介质中,壳面振动引起表面介质振动而产生声场。声场中的声压既应满足Helmholtz 波动方程,又必须满足壳体外表面处的边界条件,即表面质点的振动速度和圆柱壳表面的法线方向振动速度相等。即

式中,▽2为Laplace 算子; k0为流体波数; ρ0为流体密度。
当周围存在声介质时只有法向位移分量w 对声场有贡献。圆柱壳体在水中的耦合振动用模态展开法解[7]。对称激励时取如下形式的解
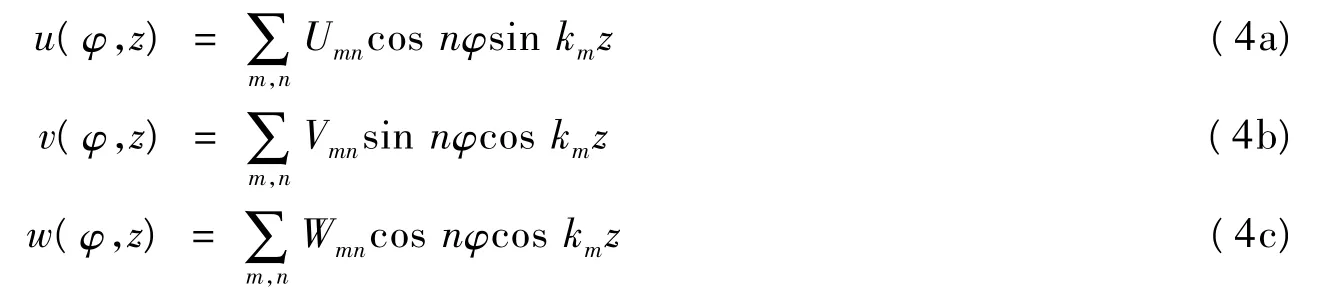
式中,- L ≤z ≤L; m 和n 都取0 ~∞; km是由边界条件确定的本征值。如取两端简支,则
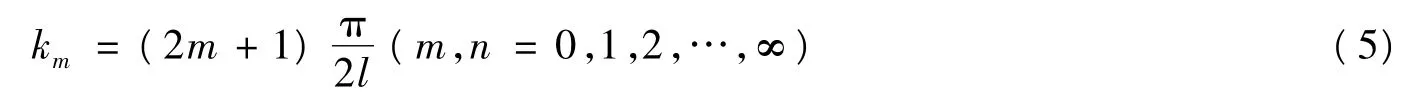
将径向激励力和壳体表面声压也展开为
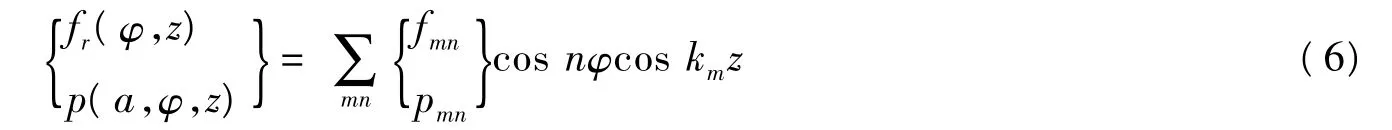
展开系数由下式给出
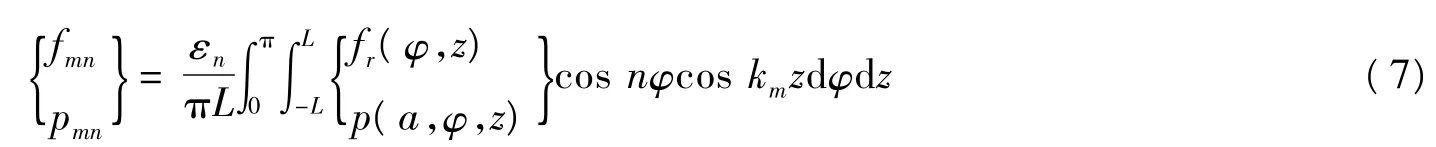
将式(4) 和式(6) 代入功能梯度材料圆柱壳的振动方程组中,可得
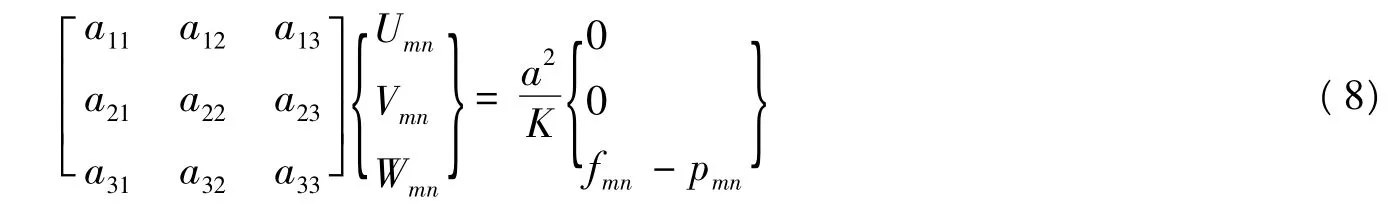
式中
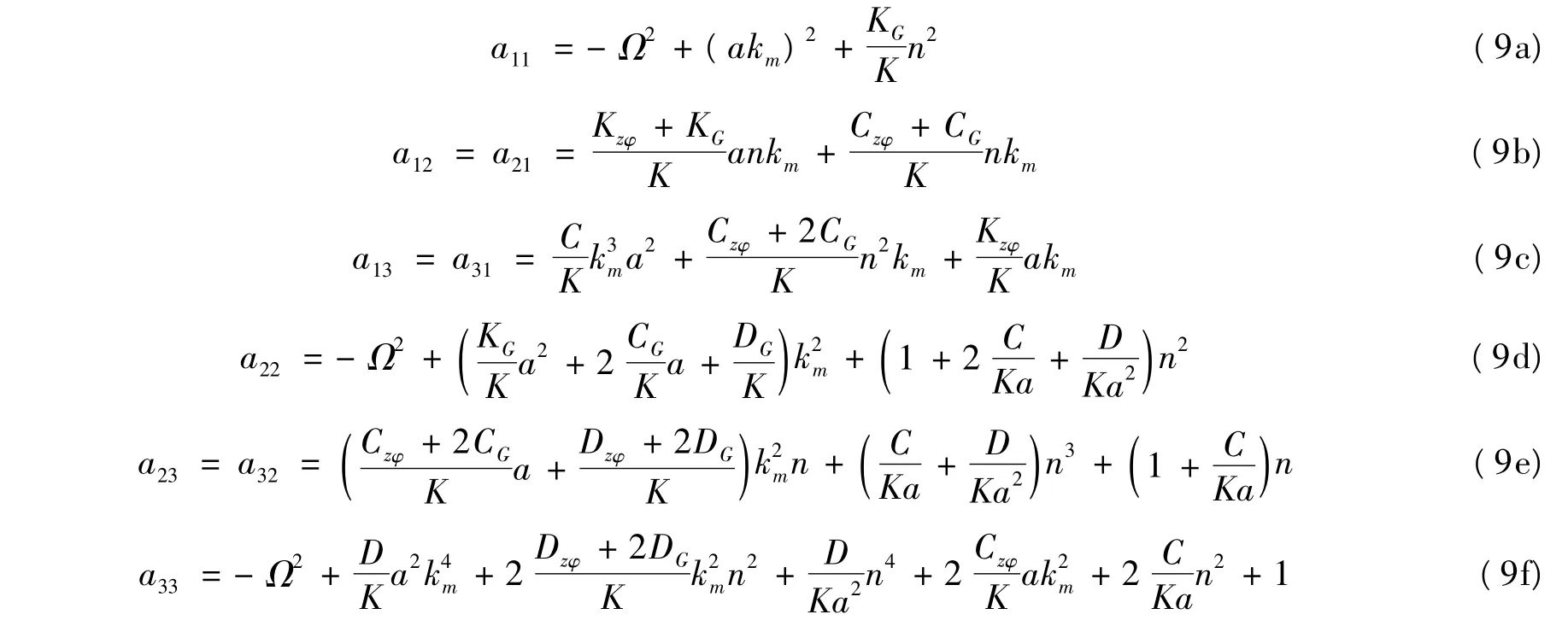
由式(8) 得到模态振动速度˙Wmn满足的方程


式中,| aij| 是模态方程(8) 中的系数行列式。假设功能梯度材料圆柱壳两端有无限延伸的刚性圆柱障板,声辐射负荷引起的表面声压[8]是

式中
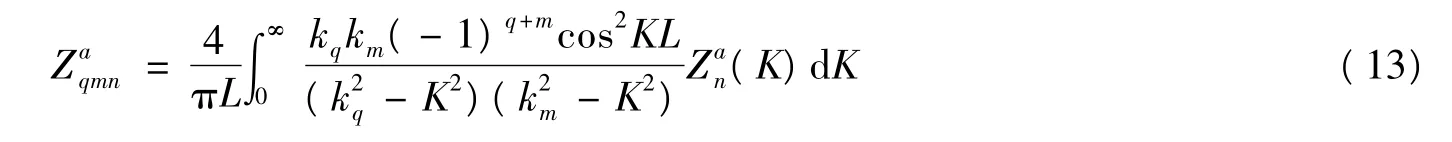
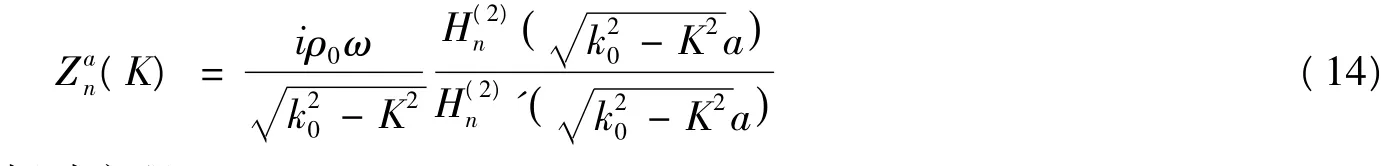
得到存在声辐射负荷时的耦合振动方程

由这个方程解出模态振动速度后即可得到有关的声学量。因此,壳体的辐射声功率是
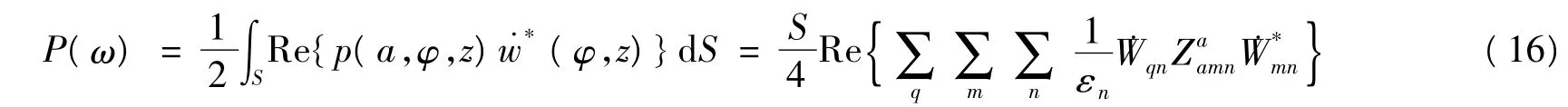
式中,*表示复共轭; S 是壳体的表面积。当n = 0 时,εn= 1 ;当n ≥0 时,εn= 2 。表面的平均振速为
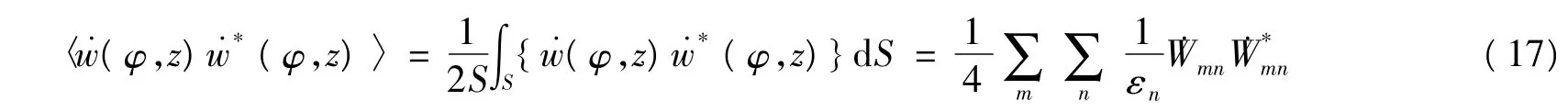
从而得到辐射效率为
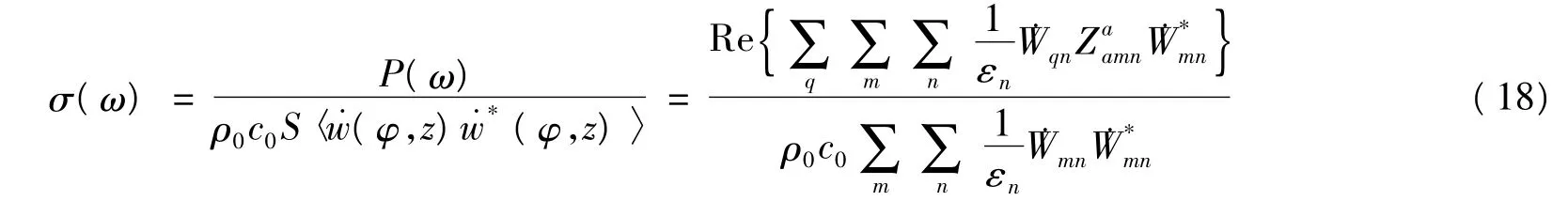
辐射声功率级定义为

表面平均振速级定义为

2 数值计算
2.1 材料参数
假设功能梯度材料圆柱壳的外表面是金属,内表面是陶瓷,中间是由不同组分的金属和陶瓷组成的复合材料,设材料常数沿厚度方向按如下规律变化[2]
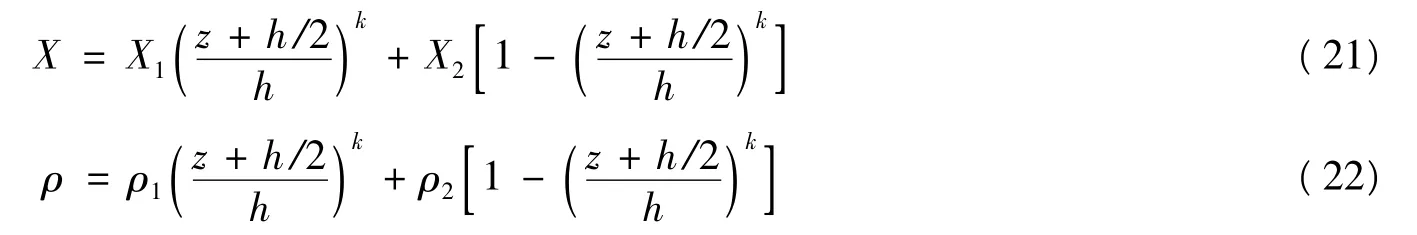
式中,X,ρ 为功能梯度材料圆柱壳的任一处材料常数和密度; X1,ρ1和X2,ρ2分别为两种不同材料对应的材料常数和密度; k 为梯度指数,它代表了材料常数随沿厚度变化的程度。设定壳材料阻尼系数η 和泊松比v 为常数,分别为0.001 和0.3。弹性模量和密度分别按(21) 式和(22) 式变化,金属和陶瓷的弹性模量和材料密度分别为Em= 70 GPa,ρm= 7.707 ×103kg/m3,Ec= 380 GPa,ρc= 3.8 ×103kg/m3。其余参数: a = 0.11 m,L = 0.165 m,h = 0.002 m,ρ0= 1 000 kg/m3,c0= 1 500 m/s。
2.2 数值仿真结果
假设功能梯度材料圆柱壳两端简支,集中激励力作用在z = 0,φ = 0,峰值F0= 1 N 的径向集中力
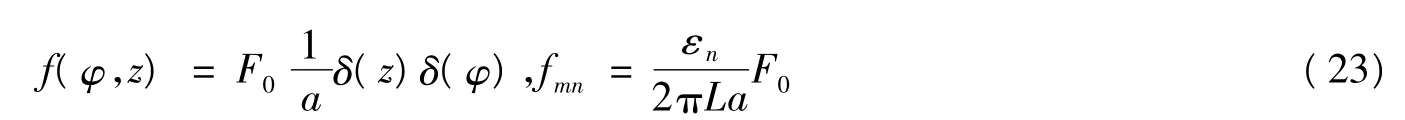
计算时忽略互耦合,只取q = m 的项。取m = 0 ~20,n = 0 ~20 的所有模态叠加。
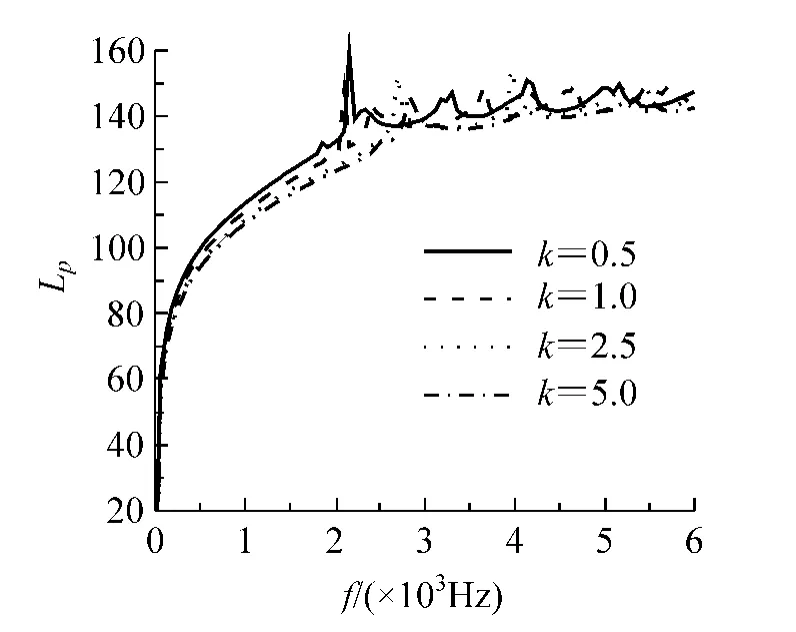
图2 辐射功率
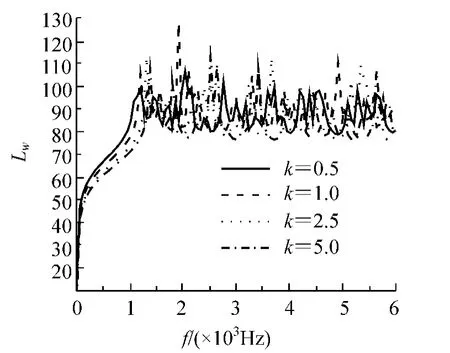
图3 平均振速
图2 ~图4 分别为不同梯度指数下功能梯度材料圆柱壳辐射功率、平均振速和辐射效率随激励频率变化的情况。从图2 可以看出,当激励频率小于2 100 Hz 时,梯度指数越大,辐射功率越小且中间没有尖峰;当激励频率大于此值时,辐射功率尖峰出现的频率不同,且高度不等。在图3 中,当激励频率小于1 100 Hz 时,梯度指数越大,平均振速越小且中间没有尖峰;当激励频率大于此值时,平均振速峰值尖峰出现的频率不同,且高度不等。从图4 中可以看出,当激励频率小于1 000 Hz 时,梯度指数对辐射效率影响很小,当激励频率大于此值时则辐射效率尖峰值发生的频率不同,而且随着频率的增加,峰值极大值有增大的趋势。因此,梯度指数对平均振速、辐射功率和辐射效率的大小及发生峰值的频率均有一定的影响。
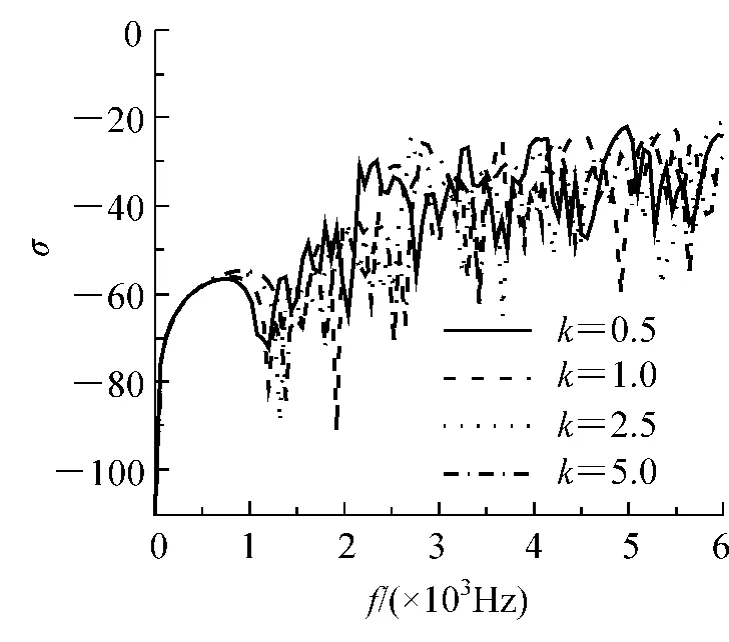
图4 辐射效率
3 结论
从有限长功能梯度材料圆柱壳振动方程出发,利用模态叠加法,推导出了圆柱壳在径向集中力激励下,平面振动平均振速和声辐射效率表达式。通过数值仿真计算了不同梯度指数下圆柱壳的平均振速、辐射功率和辐射效率。数值结果表明,梯度指数对平均振速、辐射功率和辐射效率的大小及峰值频率均有一定的影响。本文为有限长功能梯度材料圆柱壳声辐射研究提供了一种有效的分析方法。
[1]Masayuki Niino,Shuhei Maeda. Recent development status of functionally gradient materials[J]. ISIJ International,1990,30(9) :699-703.
[2]Prakash T,Ganapathi M.Asymmetric flexural vibration and thermoelastic stability of FGM circular plates using finite element method[J].Composites Part B: Engineering,2006,37:642-649.
[3]Ritesh Samadhiya,Abhijit Mukherjee,Siegfried Schmauder.Characterization of discretely graded materials using acoustic wave propagation[J].Computational Materials Science,2006,37:20-28.
[4]曹志远.功能梯度复合材料圆柱壳固有频率解[J].地震工程与工程振动,2005,26(6) :38-42.
[5]曹志远.功能梯度复合材料圆柱壳基本理论及长壳固有振动解[J].玻璃钢/复合材料,2006,4:3-6.
[6]曹志远.不同边界条件功能梯度矩形板固有频率解的一般表达式[J].复合材料学报,2005,22(5) :172-177.
[7]汤渭霖,何兵蓉.水中有限长加肋圆柱壳体振动和声辐射近似解析解[J].声学学报,2001,26(1) :1-5.
[8]Junger M C,Feit D.Sound,structures and their interaction[M].2 ed.Cambridge:The MIT Press,1986.
[9]Laulagnet B,Guyader J L.Modal analysis of a shell's acoustic radiation in light and heavy fluids[J].Journal of Sound and Vibration,1989,131(3) :397-415.
[10]Laulagnet B,Guyader J L.Sound radiation from finite cylindrical coated shells,by means of asymptotic expansion of three dimension equations for coating[J].Journal of the Acoustical Society of America,1994,96:277-286.
[11]Stephanishen P R.Modal coupling in the vibration and fluid-loaded cylindrical shells[J].Journal of the Acoustical Society of America,1982,71:813-823.
[12]Wu C J,Chen HL,Huang XQ.Vibroacoustic analysis of a fluid-loaded cylindrical shell excited by a rotating load[J].Journal of sound and vibration,1999,225(1) :79-94.
[13]Wu Lanhe.Thermal buckling of a simply supported moderately thick rectangular FGM plate[J].Composite Structures,2004,64:211-218.
- 石家庄铁道大学学报(自然科学版)的其它文章
- 吊杆索力的计算方法与应用研究
- 基于移动荷载分析的沥青路面结构优化设计
- 曲曲连接新型缓和曲线线形动力特性分析
- 重载铁路顶进线路加固技术

