基于模糊理论的城市铁路客运站换乘衔接综合评价
梅 丽, 邓 念
( 西南交通大学 交通运输与物流学院,四川 成都 610031)
0 引言
城市铁路客运站是城市对外交通联系和对内交通联系的重要结点,该片区是城市交通最复杂、人口最密集的区域之一,快速疏散大量的旅客和市内其他人员,是保证该片区交通快捷、有序进行的关键。对城市铁路客运站换乘衔接方案进行综合评价,其目的是能够更加准确的认识换乘系统内部的特征及其规律,为协调换乘系统内各种交通方式的衔接关系和场站布局提供研究指标和决策依据[1]。随着社会经济的快速发展,城市铁路客运站的换乘衔接已经由简单的交通方式,发展为集地铁、公交车、出租车、长途客运、自行车等的综合交通方式,这样也使得影响铁路客运站换乘衔接的评价因素越来越多。这些因素中有一部分是可以由具体数字度量的定量指标,而另一部分却不能用数字度量,只存在定性关系。应用引入了三角模糊数的层次分析法,结合模糊综合评价法对城市铁路客运站换乘衔接进行评价可以有效解决这种问题。以成都站作为研究对象,进行实证分析。成都站为成都枢纽主要客运站,目前成都站主要的换乘交通方式是地铁、公共汽车、出租车、长途汽车、私人及社会车辆等。
1 评价体系的建立
通过分析国内外关于换乘衔接评价指标体系建立的情况,结合成都站的具体情况,在综合性、实用性、可比性等的原则下,以乘客综合效用、换乘设施配置、衔接协调性和换乘效率四个方面作为一级指标;以换乘舒适度、换乘可靠性、换乘安全性、换乘经济性等15 个方面作为二级指标,建立能够反映城市铁路客运站换乘衔接的综合性评价指标体系。评价体系如图1 所示。
2 城市铁路客运站换乘衔接评价模型
2.1 基于三角模糊数的层次分析法确定权重
2.1.1 三角模糊数定义
定义1 设F( H) 为三角模糊集,其中H 为三角模糊数,由于其隶属度函数为三角形,则可表示为H =( l,m,p) ,其中,l,m,p 分别为三角模糊数H 的最小元素、中间元素、最大元素,且0 ≤l ≤m ≤p。
定义2[2]对于H = ( l,m,p) 这样的三角模糊数,将其转化为对应的非模糊数的公式为S( H) = ( l,m,p) /4,其中l,m,p ≥0。

图1 评价指标体系
定义3[3]对于三角模糊数Hij和Hji,其中Hij= ( lij,mij,pij) 、Hji= ( lji,mji,pji) ,如果lij+ lji= mij+mji= pij+ pji= 1,lij,mij,pij≥0,i,j ∈N,则称三角模糊数Hij和Hji互补。
2.1.2 构造判断矩阵
判断矩阵就是表述每一层次中各要素相对上一层次某要素的相对重要程度。在两两比较中很难判断指标间的重要程度,因此本文在科学性、可靠性等原则下采用比较符合中国人思维习惯简便实用的判
断尺度即0.1 ~0.9 标度法[4],对不同指标进行比较,从而构造判断矩阵。
2.1.3 计算权重
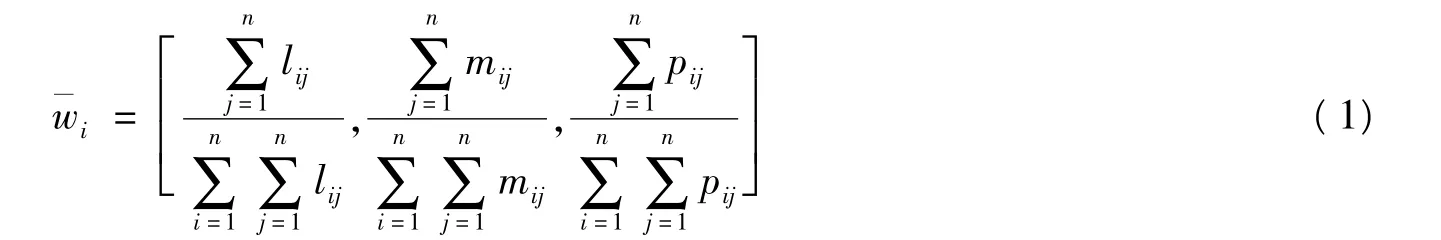
然后根据各个权重的三角模糊数,利用定义2 计算各模糊数对应的非模糊数,即其对应指标的最终权重wi= ( lij+2mij+ pij) /4 。
2.1.4 一致性检验[5]
满足定义3 且hii= ( lii,mii,pii) = (0.5,0.5,0.5) 的hii所组成的矩阵( hij) 称为模糊判断矩阵。如果hij>hji,则称hi比hj重要,记为hi>hj。若模糊判断矩阵( hij) 满足:当hi>hj,hj>hk时,有hi>hk。则称矩阵阵( hij) 具有一致性。
2.1.5 各指标权重计算结果
根据上述步骤,采用专家打分法确定判断矩阵,计算出各指标的权重结果如表1 ~表4。

表1 成都站综合评价判断矩阵
W¯A= [(0.318,0.300,0.287) ,(0.227,0.250,0.245) ,(0.136,0.150,0.181) ,(0.318,0.300,0.287) ];WA=(0.301,0.243,0.154,0.301) 。

表2 成都站乘客综合效用判断矩阵
W¯B= [(0.344,0.325,0.313) ,(0.219,0.225,0.229) ,(0.281,0.275,0.271) ,(0.156,0.175,0.188) ];WB=(0.327,0.224,0.276,0.173) 。

表3 成都站换乘设施配置判断矩阵
W¯C= [(0.250,0.250,0.250) ,(0.250,0.250,0.250) ,(0.250,0.250,0.250) ,(0.250,0.250,0.250) ];WC= (0.250,0.250,0.250,0.25) 。

表4 成都站衔接协调性判断矩阵
W¯D= [(0.354,0.325,0.316) ,(0.231,0.238,0.232) ,(0.277,0.288,0.284) ,(0.138,0.150,0.168) ];WD= (0.330,0.234,0.284,0.152) 。

表5 成都站换乘效率判断矩阵
W¯E= [(0.459,0.444,0.415) ,(0.324,0.311,0.321) ,(0.216,0.244,0.264) ];WE=(0.441,0.317,0.242) 。
由以上计算结果可以看出,全部判断矩阵满足一致性检验。因此,计算出的各指标权重值具有一定的可靠性和准确性。
2.2 模糊综合评价模型
2.2.1 建立评判集通过分析国内外关于换乘衔接评价等级的研究,结合成都市的实际情况,将城市铁路客运站的交通换乘衔接评价等级划分为好、较好、一般、较差、差5 个等级。因此,建立本次模糊评价的评判集V = ( V1,V2,V3,V4,V5) =( 好,较好,一般,较差,差) 。
2.2.2 单因素模糊评价
对与成都站换乘衔接评价有关的各种因素进行调查,通过专家打分法和换乘乘客问卷调查法,将收集到的数据、资料进行整理和分析,单因素评价结果如下:
(1) 乘客综合效用RB。①换乘舒适度RB1= (0.27,0.27,0.25,0.2,0.01) ;②换乘可靠性RB2=(0.35,0.30,0.13,0.14,0.08) ;③换乘安全性RB3= (0.20,0.44,0.16,0.15,0.05) ;④换乘经济性RB4=(0.28,0.25,0.25,0.15,0.07) 。
(2) 换乘设施设置RC。①站场类设施RC1= (0.30,0.53,0.12,0.03,0.02) ;②集散类设施RC2=(0.08,0.48,0.26,0.08,0.10) ;③通道类设施RC3= (0.12,0.41,0.32,0.10,0.05) ;④信息类设施RC4=(0.40,0.34,0.12,0.08,0.06) 。
(3) 换乘协调性RD。①换乘能力匹配RD1= (0.23,0.42,0.23,0.10,0.02) ;②排队服务设施RD2=(0.21,0.61,0.14,0.03,0.01) ;③换乘布局协调度RD3= (0.20,0.54,0.14,0.10,0.02) ;④换乘方式种类RD4= (0.80,0.10,0.05,0.02,0.03) 。
(4) 换乘效率RE。①换乘时间RE1= (0.14,0.32,0.34,0.15,0.05) ;②换乘距离RE2= (0.35,0.48,0.10,0.04,0.03) ;③流线绕行程度RE3= (0.40,0.34,0.20,0.05,0.01) 。
2.2.3 模糊综合评价[6]
通过以上的判断矩阵得出各指标对应的权重,从而进行模糊综合评价,其公式表示为

式中,vj表示评价对象对评价集中第j 个元素的隶属度,也就是评价结果。
根据上述对成都站换乘衔接评价二级指标的分析以及权重计算,应用模糊评价算法得出每个一级指标的n 个因素的综合评价矩阵。B = WBRB= (0.270,0.320,0.198,0.164,0.047) ;C = WCRC= (0.225,0.440,0 .205,0.073,0.058) ;D = WDRD= (0.303,0.450,0.156,0.071,0.019) ;E = WERE= ( 0. 270,0.376,0.230,0.091,0.034) 。
2.2.4 模糊综合评价结果
将一级指标层各因素的综合评价矩阵组合得到目标层综合评价矩阵R,其中R= ( B,C,D,E)T,目标层 综 合 评 价 结 果 如 下: V = WAR =(0.301,0.243,0.154,0.301)(0.264,0.386,0.203,0.105,0.041) 。
根据计算结果,运用最大隶属原则[6]进行判断,其判断原则为:对于评价结果S,若S 中最大的元素为sk,则该评价结果隶属于sk对应的等级,得出成都站换乘衔接模糊综合评价的结果为“较好”。
3 结语
考虑到影响城市铁路客运站换乘衔接评价的因素具有不确定性和一定的模糊性,将城市铁路客运站的换乘衔接评价结果分为五个等级:好、较好、一般、较差、差,同时将三角模糊数引入层次分析法中,建立了城市铁路客运站换乘衔接评价指标体系和判断矩阵,运用模糊综合评价模型,得出其评价值为“较好”。引入三角模糊数的AHP-模糊综合评价法全面考虑了影响系统安全的各种因素,将定性和定量的分析有机地结合起来,既能够充分体现评价因素和评价过程的模糊性,又克服了传统经验类比较法的局限性[7],为其评价提供了一种定量的分析方法。这种评价方法能够更客观、更科学的评价城市铁路客运站的换乘衔接方案,评价结果可靠性更高。同时通过数据分析,可找出影响城市铁路客运站换乘衔接的关键因素,从而进行针对性的改善。
[1]宗婷,张生瑞,霍东方,等.城市客运交通换乘枢纽评价研究[J].水利与建筑工程学报,2007,5(3) :68-71.
[2]许谦.确定模糊评价综合因素权重的一个方法[J].大学数学,2005,21(1) :99-103.
[3]龚艳冰,陈森发.三角模糊数互补判断矩阵的一种排序方法[J].模糊系统与数学,2008,22(1) :127-131.
[4]杜栋.基于0.1 ~0.9 标度的AHP 再研究[J]. 系统工程与电子技术,2001,23(5) :36-38.
[5]苏世彬,黄瑞华.基于三角模糊数的属性层次模型[J].系统工程理论与实践,2006(12) :115-119.
[6]李鸿吉.模糊数学基础及实用算法[M].北京:科学出版社,2002.
[7]欧阳展.大型综合客运枢纽交通协调模型与评价方法的研究[D].北京交通大学交通运输学院,2008.

