基于三角模糊数的TOPSIS 评价方法在新建铁路线路选择中的应用
向 隅
( 武汉铁路职业技术学院 电子与电气工程系,湖北 武汉 430205)
铁路线路方案的评价及选择是在铁路建设前期需要解决的重要问题。不同线路方案的选择,不仅决定投资费用、线路设计的质量、工程造价和运营条件,而且对方案所经过地区和城市的经济、规划、环境和其他社会条件也有不同层次的影响,并最终决定一条新建铁路的综合效益。采用正确、合理的指标体系对新建铁路方案这一多目标进行科学评价决策,能够使铁路工程这一重大基础设施建设做到投资合理、运营效果显著,达到经济的、社会的、环境的最佳综合效益的结果。
对于多目标决策问题,目前比较流行的解决方案是层次分析法( AHP 分析法) 或模糊层次分析法( FAHP 分析法) ,2008 年中南大学吴小萍等人将AHP 方法用于铁路环境选线评价指标体系,并建立了决策模型;李艳红、齐永国使用AHP 方法对湖杭段的线路选择进行了研究,并建立了模型,通过分析得到了与实际一致的结果[1]。栾德峰、田元福使用模糊AHP 分析法对铁路项目评标进行了研究[2]。
然而,AHP 方法和模糊综合评判法在将专家意见由定性向定量转化时均由于表达专家意见不完整性而最终可能导致结果不符合实际情况[3],而且运用AHP 分析法和FAHP 分析法通过1 -9 标度建立的判断矩阵要进行一致性检验,当判断矩阵不一致时,需对判断矩阵进行调整,其计算量大且复杂。研究借助于三角模糊数良好的数学性质,并与TOPSIS 法相结合,将新建线路选线中一些难于直接定量的指标和专家意见定量化,从而对新建铁路线路走向方案作出合理的排序,为新建铁路线路走向决策提供科学依据。
1 基于三角模糊数的TOPSIS 分析法的基本原理
1.1 三角模糊数定义及运算规则[4]
定义1:设在实数域R 上的一个模糊数~p,定义一个隶属函数:~u( x) :R→[0,1],x∈R,若特征函数( 隶属函数) ~u( x) 表示为
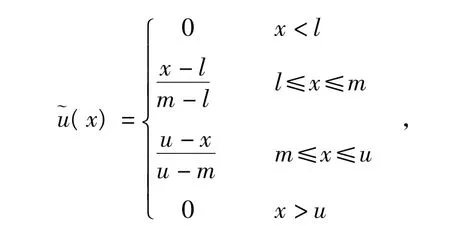

图1 三角模糊数分布图
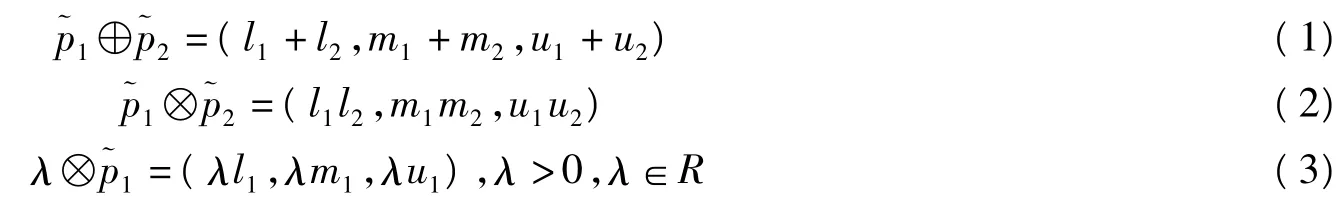
式中,符号⊕和⊗表示模糊数的加法和乘法运算。
定义3:由三角模糊数构成的矩阵称为三角模糊矩阵。

1.2 基于三角模糊数的TOPSIS 分析方法的评价原理
假设参与评价的方案集为P=[p1,p2,…,pm],即有m 个方案供选择;评价指标集为B =[b1,b2,…,bn]。在评价过程中,所需的信息有: 三角模糊指标权重矩阵和三角模糊指标评价矩阵=m×n( i=1,2,…,m;j=1,2,…,n) ,其中为指标bi的权重评价值为方案pi之指标bj的评价值。
Step1:建立三角模糊指标权重矩阵。
专家给出指标bi权重的三角模糊数。
专家给出指标bi的评价语言经转换后的三角模糊数为表示专家给出指标bi权重的最保守值,表示专家给出指标bi权重的最可能值,表示专家给出指标bi权重的最高值。则指标权重的三角模糊矩阵为
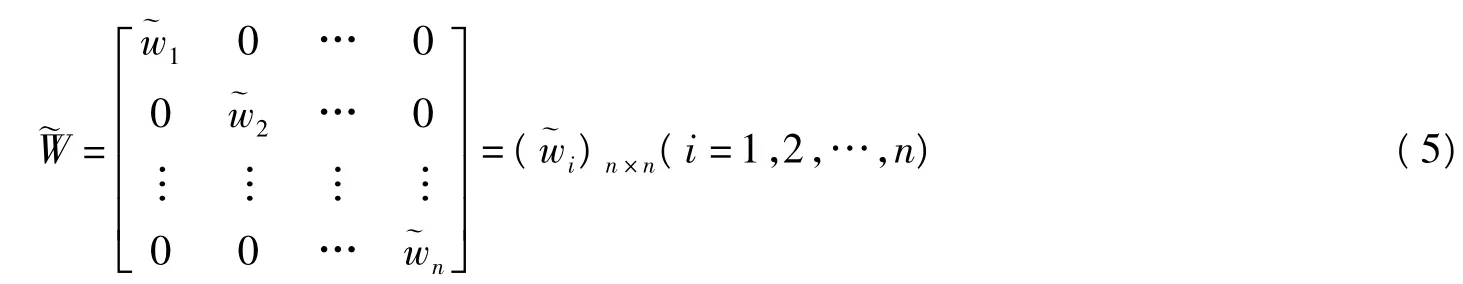
Step2:建立三角模糊指标评价矩阵。
对于被评方案pi之指标bj,专家给出的评价为=( lij,mij,uij,lij) 表示专家对方案pi之指标bj的最保守评价,mij表示专家对方案pi之指标bj给出的最可能评价,uij表示专家对方案pi之指标bj给出的最高评价,则专家对m 个方案的n 个指标进行评价构造的模糊矩阵为

Step3:构建评语集。
以程度语言构建评语集,并将评语集转化为三角模糊数。权重与指标评语对应的三角模糊数如表1所示[5]。
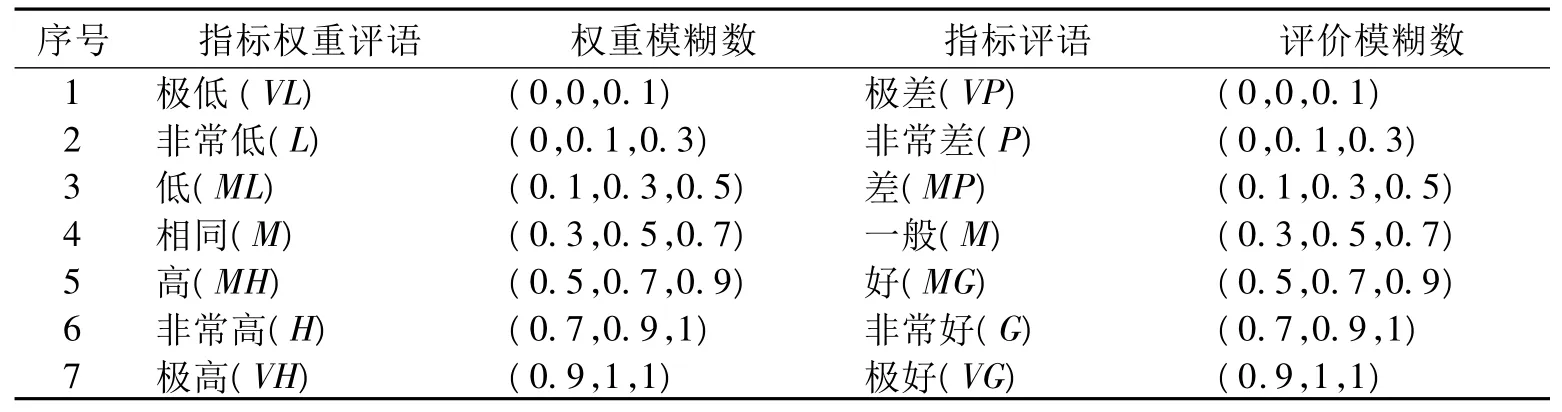
表1 权重与指标评语的模糊数对照表
Step4:把三角模糊数转化为清晰值。
对于清晰数,采用公式(7) 计算期望值[6];对于模糊数,采用三角模糊数的隶属函数——公式(8) 来计算模糊评价期望值[7]。

a 为区间最小值,b 为区间最大值。

转化后的W 和R 分别为W=( wi)n×n( i=1,2,…,n) 和R=( rij)m×n( i=1,2,…,m;j=1,2,…,n) 。Step5:对矩阵进行归一化处理。
由于各个指标的量纲可能不同,需对W 和R 分别进行归一化处理。W 按公式(9) 进行归一化处理;R按公式(10) 起进行归一化处理。

Step6:形成加权判断矩阵。

式中,fij= wjrij,i = 1,2,…,m;j = 1,2,…,n 。
Step7:根据加权判断矩阵获取评估目标的正负理想解。
正理想解:

负理想解:

式中,J*为效益型指标,J′ 为成本型指标。
Step8:计算各目标值与理想值之间的欧氏距离。
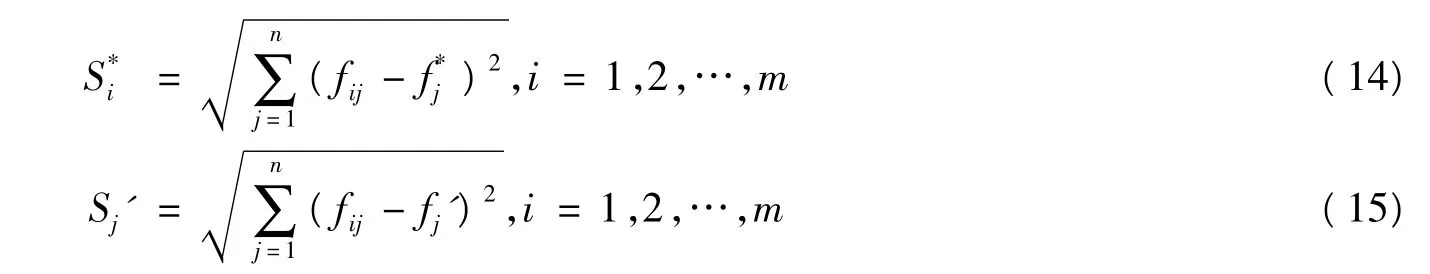
Step9:计算各个目标的相对贴近度。

Step10:依照相对贴近度的大小对目标进行排序,形成决策依据。
2 评价模型的应用
2.1 构建新建铁路线路选择评价递阶层次结构
铁路建设投资巨大,而且一经建设,不可轻易改动。尤其在当今中国铁路运输高速发展,高速铁路线的建设对中国经济的发展有着巨大的影响,新建铁路的线路选择更是要考虑多种复杂因素。影响铁路线路走向的基本因素主要有:①社会政治经济意义;②施工工程量的大小及工程费的多少;③施工对环境影响;④预期经济效益和运营量;⑤自然条件等等。结合工作中的实际情况,并参阅其他一些相关资料[1,8-10],建立图2 所示的新建铁路线路选择评价递阶层次结构,包括目标层A、评价指标层B 和方案层C。
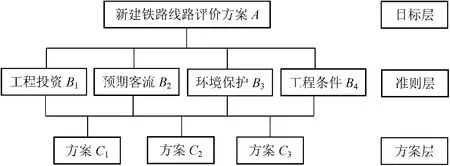
图2 新建铁路线路选择评价递阶层次结构
2.2 模型求解
(1) 利用德尔菲法则,生成集结后的权重矩阵和三角模糊综合评价矩阵评价矩阵群体偏好矩阵。
初始条件:根据图2 的专家群决策结果经过公式(5) 、(6) 生成三角模糊权重矩阵和三角模糊综合评价矩阵,经过公式(17) 、(18) 运算得到加权的三角模糊权重和三角模糊综合评价矩阵,如表2 所示。

表2 权重和评价

(2) 对于表2 中的数据,经过公式(7) 和公式(8) 的运算得到综合评价和指标权重期望值,如表3 所示。

表3 综合评价和指标权重期望值
(3) 按照表3 中的数据,根据公式(9) 、(10) 、(11) 、(12) 和(13) 求得正负理想解。

3 结语
(1) 铁路线路的走向是在铁路建设前期必需解决的问题。为了对新建铁路线路的走向选择这一多目标问题进行决策,结合工作中的实际情况,构建由工程投资、预期客流、环境保护和工程条件四个指标构成的新建铁路线路走向的选择评价指标,运用三模糊数确定了综合评价矩阵和权重期望值,运用TOSSIS方法确定了新建铁路线路的走向。
(2) 在评价指标中,除工程预期投资这一定量指标可根据铁路CAD 软件求得具体的数值外,对其它指标的评价均为定性评价,评价语言带有模糊性,三角模糊数很好地解决了将定性问题定量化。为了减少主观原因造成对评价结果的影响,采用Delphi 法则即专家组评判方法,使定性评价更加合理,更加切合实际。
(3) 从评价结果看,指标的设立能综合地反映新建铁路线路选择评价条件; 使用三角模糊数的TOPSIS 评价方法对新建铁路线路走向方案的选择评价,数据科学、可靠,为决策者提供了更加切合实际的选择依据。
(4) 三角模糊数的TOPSIS 评价方法与AHP 和FAHP 方法相比,减少了因人的主观因素对决策结果产生的影响。
[1]李艳红,齐永国.层次分析法在铁路线路方案比选中的应用[J].铁道运输与经济,2009,9:86-87.
[2]栾德峰,田元福.模糊综合评判法在铁路项目评标中的应用[J].价值工程,2008,11(11) :100-101.
[3]廖勇.基于三角模糊数的铁路客运站选址方案评价方法[J].中国铁道科学,2009,30(6) :119-125.
[4]杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,2003.
[5]陈晓红,阳熹.一种基于三角模糊数的多属性群决策方法[J].系统工程与电子技术,2008,30(2) :278-282.
[6]李家军,杨莉.对隶属函数确定方法的进一步探讨[J].贵州工业大学学报:自然科学版,2004,33(6) :1-4.
[7]韩庆兰,杨涛.AHP 算法和三角模糊数在虚拟企业的盟员选择中的应用[J].运筹与管理,2003,12(1) :17-21.
[8]薛波,李远富,胡英婕.铁路线路方案模糊优化模型的改进研究[J].系统工程理论与实践,2003,11(11) :125-129.
[9]李远富,薛波,邓域才.铁路线路方案模糊优化模型及其应用研究[J].系统工程理论与实践,2001,6(6) :108-113.
[10]苏印,李铁柱.国际多式联运线路选择的方法研究[J].交通运输系统工程与信息,2006,6(2) :91-94.

