一类不确定非线性系统的动态面输出调节方法

孟桂芝， 马克茂

(1.哈尔滨工业大学控制与仿真中心，黑龙江哈尔滨 150001;2.哈尔滨理工大学应用数学系，黑龙江哈尔滨 150080)

一类不确定非线性系统的动态面输出调节方法

孟桂芝1，2， 马克茂1

(1.哈尔滨工业大学控制与仿真中心，黑龙江哈尔滨 150001;2.哈尔滨理工大学应用数学系，黑龙江哈尔滨 150080)

针对一类由线性中性稳定的外系统驱动的具有未建模动态和外界扰动的非线性不确定系统的输出调节问题，结合动态面控制法和内模原理提出一种具有动态面控制的设计方法。根据非线性输出调节问题可解的必要条件，运用状态变换和标准内模将输出调节问题转化为镇定问题。运用动态面控制法将一阶滤波器引入反步设计中，避免了反步设计中所存在的“膨胀项”。引入具有误差的内模方程，根据外系统信息设计出控制律镇定闭环系统。仿真结果表明，得到的控制器能够实现闭环系统的信号全局最终有界且跟踪误差在期望的任意精确度范围内。

非线性系统;输出调节;内模;反步设计法;动态面控制

0 引言

输出调节问题就是控制系统的输出，以达到渐近跟踪给定的轨线或渐近扰动抑制的目的。与常规的轨道跟踪或扰动抑制问题相比，输出调节问题的描述特点是参考输入和扰动并不完全可知。线性系统的输出调节问题在20世纪70年代被提出并已经得到完整的解决［1－2］。对解决线性系统输出调节问题，内模原理是一种强有力工具［3－4］。近年来，非线性系统的输出调节问题及内模原理一直被广泛关注，对于系统中不确定性的处理使得这个问题更具挑战性。

目前，已有众多学者对非线性系统输出调节问题及内模原理进行研究。文献［5］针对一类可镇定的线性化系统，在其存在一个确定的可控的不变流形的假设条件下，给出了局部全信息解存在的充要条件。文献［6］利用高增益内模解决了非线性系统的半全局输出调节问题。文献［7］针对不可线性化的非线性输出反馈系统，解决了全局结构稳定调节问题。当外系统存在不确定参数时，文献［8－9］通过构造自适应内模解决了一类非线性系统的半全局、全局鲁棒输出调节问题。当系统中存在未知常参数时，文献［10－11］应用自适应技巧去解决输出调节或扰动抑制问题。

以上系统的不确定性大都限制在由未知常参数引起的参数不确定性上。然而，在实际系统中，大量存在由测量误差、未建模误差、外界扰动或模型简化引起的非线性不确定函数［12－13］。在实际工程中，对受控对象建立精确的模型有时是困难的，因此研究具有未建模动态和外界干扰的不确定系统的控制问题具有重要的实际意义。对于非线性不确定系统，反步(backstepping)设计法是一种行之有效的系统化的控制器设计方法［14］，但是反步设计法存在“计算膨胀”问题，为解决“计算膨胀”问题和降低虚拟控制为光滑信号的要求，文献［15］提出动态面控制法。由于动态面控制法中包含低通滤波器，而这些滤波器允许对象数学模型不可微，因此避免了“膨胀项”的产生，减少了计算量，易于实现。

近年来，动态面控制法引起了学者们极大的兴趣。文献［16］针对具有非匹配不确定的严格反馈非线性系统，利用动态面控制和二阶滑模设计出控制器实现了不确定系统任意小的跟踪误差。文献［17］将输入状态稳定(input-to-state stability，ISS)理论和动态面控制法结合解决了具有未知死区和摄动的非线性纯反馈系统。这些结果都是针对反馈系统而言的，对输出调节问题目前还没有应用。

本文针对一类具有未建模动态和外界干扰的非线性不确定系统，考虑了渐近追踪的输出调节问题。本文采用反步法和动态控制法结合去设计控制器，前n－1步采用动态面控制法可避免项的爆炸(terms explosion)。第n步引入具有误差的内模方程，利用外系统信息镇定控制项，给出控制器，提高了系统的鲁棒性、快速性和精确度。

1 问题描述

考虑如下形式的非线性不确定系统

其中:x=［x1，x2，…，xn］T∈n为系统状态;u为控制输入;y为输出;gi(i=1，2，…，n)为已知C1光滑函数，Δfi∈n×m(i=1，2，…，n)为包含未建模动态和外界干扰的不确定项，为未知连续函数。Ri(w)、Di(w)分别代表参考输入、非期望扰动，是已知的光滑的非线性函数。w∈Ωm为外系统信号，由以下被称为外系统的线性自治微分方程

生成，其中Ω为包含原点的任意的确定已知的紧致子集。

假设1 外系统是中性稳定的。

假设2 存在光滑函数pi(x1，x2，…，xi)，使得

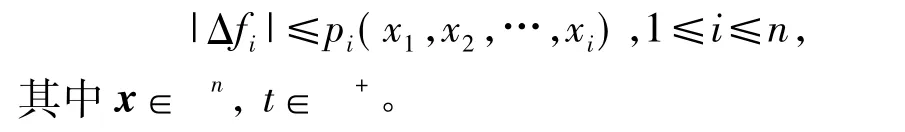
本文要解决的输出调节问题可描述如下:针对系统(1)和系统(2)，在假设1、假设2成立的条件下，设计反馈控制器u(t)使闭环系统信号全局一致有界，且跟踪误差|e|在任意给定的期望的范围内。

2 内模设计

对于系统(1)和系统(2)，容易看出存在一个全局定义解，即

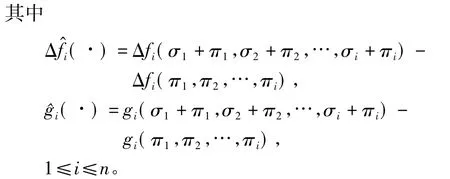
注1 在假设2条件下，一定存在已知光滑函数 φi(σ1，σ2，…，σi)使得

在假设3条件下，具有输出α(w)的外系统可浸入到如下可观测线性系统

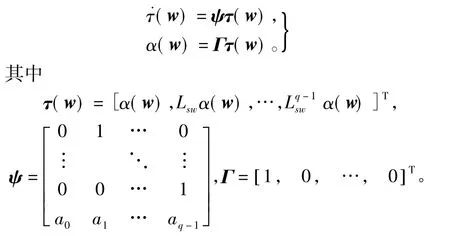
基于线性观测器理论，对任意一个可控对［G，H］，其中G∈q×q为 Hurwitz矩阵，H∈q。又［ψ，Γ］可观，从而 Sylvester方程Tψ－GT=HΓ有唯一的非奇异解T，令 φ=ΓT－1∈1×q，则 φ使得外系统被浸入到下列系统

收集转染后的对数生长期的SUNE-1细胞，提取蛋白后，用BCA蛋白质测定试剂盒定量测定蛋白浓度。通过SDS-PAGE分离后，将蛋白转移至PVDF膜中，BSA液封闭30 min，EGFR一抗(1∶1 100)4℃孵育过夜，用含有的TBST溶液洗膜3次，每次10 min，在室温下孵育二抗(1∶5 000)，封闭1 h。使用ECL显影液检测目标蛋白的表达水平，GAPDH用于蛋白内参对照;实验重复3次。

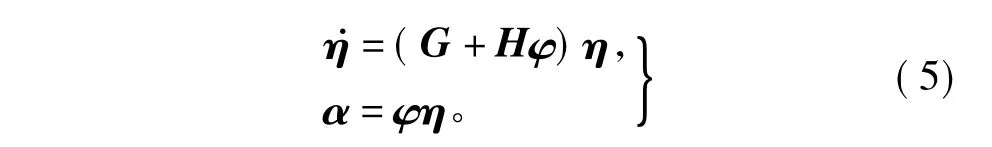
式(5)被称为内模的标准参数化形式。

基于内模的标准参数化形式，根据确定性等价原则，提出具有误差系统的内模形式

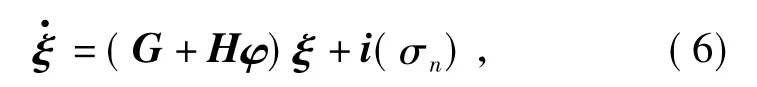
作为调节器的内模部分，其中i(·)待设计参数。

3 控制器设计

对于系统(3)、系统(5)、系统(6)，前n－1步采用动态面法设计控制器，能有效防止项的爆炸。

Step1 设S1=σ1－ σ1d，不妨取 σ1d=0。选取Lyapunov函数

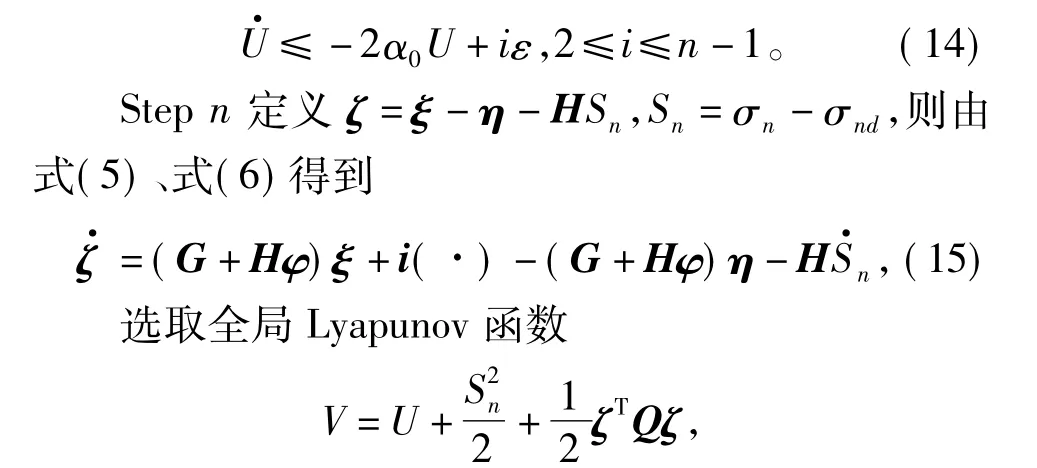
其中Q为正定对称矩阵，满足GTQ+QG=－2kI，其中k＞0为待设计常数。则V沿式(3)、式(15)对时间的导数为为任意小。由于S1=σ1=e，可以使所设计的调节误差任意小，同时使所设计的内模状态任意逼近标准化内模状态。由上述分析可得到如下定理:

定理1对于被控系统(1)和外系统(2)，如果假设1、假设2和假设3满足，则存在式(11)、式(17)、式(19)解决非线性系统的输出调节问题，并使闭环系统的信号全局最终有界，调节误差渐近趋于零。

4 仿真算例

可验证系统(27)与系统(28)满足假设1、假设2和假设3，且调节器方程有解为

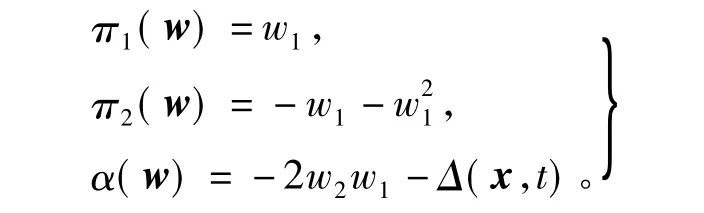
取外界扰动 Δ(x，t)=0.05sin(2t)，令 τ(w)=［α(w)，Lswα(w)］，则外系统(28)可浸入到如下可观测线性系统

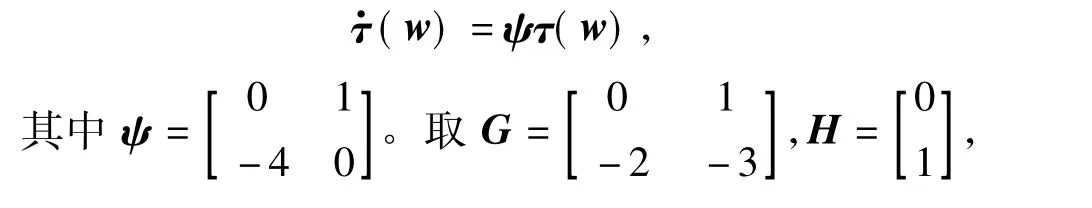
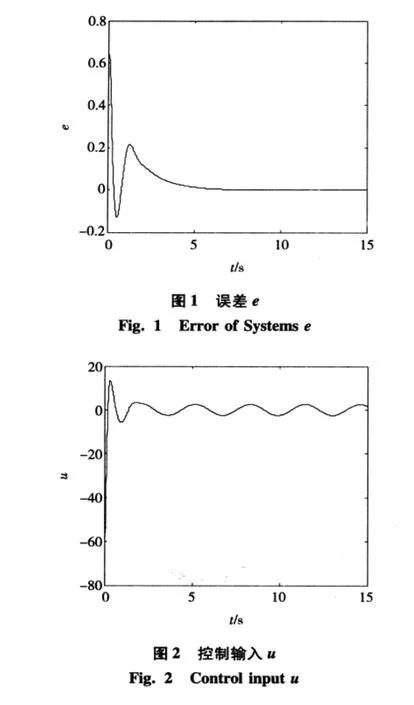
由仿真结果可以看出，误差趋近于零。理论分析可知，在一般情况下，由于δ≠0，可以通过调整控制器参数使得误差在期望的范围内。控制器简单，计算量小，仿真结果表明所给出的控制方法有效性。

5 结语

非线性不确定系统的输出调节问题一直是控制理论研究的热点和难点。本文针对一类由线性中性稳定的外系统驱动下的具有未建模动态和外界扰动的非线性系统，研究了其鲁棒输出调节问题。所设计的控制器能够维持全局信号最终有界的情况下，调解误差变量渐进趋于零。在反步设计中引入动态面控制法，由于动态面控制法中采用的低通滤波器允许对象数学模型不可微，因此避免了对虚拟控制反复求导数，减少了计算量。在构造内模方程时，由于不确定性的影响，提出具有误差的内模方程。由非线性的外系统驱动下的此类不确定系统的鲁棒调节器尚有待进一步研究。

［1］ FRANCIS B A，WONHAM W M.The internal principle of control theory［J］.Automatica，1976，12(5):457 －465.

［2］ DAVISION E J.The robust control of a servomechanism problem for linear time － invariant multivariable systems［J］.IEEE Transactions on Automatic Control，1976，21(2):25 －34.

［3］ PRISCOLI F D.Output regulation with nonlinear internal model［J］.Systems and Control Letters，2004，53:177 －185.

［4］ 程代展，董亚丽.输出调节与内模原理［J］.自动化学报，2003，29(2):284－295.

CHENG Daizhan，DONG Yali.Output regulation and internal model principle［J］.Acta Automatica Sinica，2003，29(2):284－295.

［5］ ISIDORI A，BYRNES C I.Output regulation of nonlinear systems［J］.IEEE Transactions on Automatic Control，1990，35(2):131－140.

［6］ BYRNES C I，ISIDORI A.Nonlinear internal model for output regulation［J］.IEEE Transactions on Automatic Control，2004，49(12):2244－2247.

［7］ SERRANI A，ISIDORI A.Global robust output regulation for a class of nonlinear systems［J］.Systems and Control Letters，2000，39:133 －139.

［8］ SERRANI A，ISIDORI A.Semiglobal nonlinear output regulation with adaptive internal model［J］.IEEE Transactions on Automatic Control，2001，46(8):1178 －1194.

［9］ 陈作贤，季海波.具有自适应内模的非线性系统输出调节［J］.控制与决策，2009，24(5):759 －763.

CHEN Zuoxian，JI Haibo.Output regulation for a class of nonlinear systems with adaptive internal model［J］.Control and Decision，2009，24(5):759 －763.

［10］ XI Zairong，DING Zhengtao.Global adaptive output regulation of a class of nonlinear systems with nonlinear exosystems［J］.Automatica，2007，43(1):143 －149.

［11］ DING Zhengtao.Output regulation of nonlinear systems with nonlinear exosystems［J］.IEEE Transactions on Automatic Control，2006，51(3):498－503.

［12］ 郑剑飞，冯勇，杨旭强.非匹配不确定多变量系统高阶终端滑模控制［J］.电机与控制学报，2009，13(1):117 －122.

ZHENG Jianfei，FENG Yong，YANG Xuqiang.High －order terminal sliding mode control of mismatched uncertain multivariable systems［J］.Electric Machines and Control，2009，13(1):117－122.

［13］ 刘陆洲，肖建，王嵩.良好非线性模型辨识及其内模控制［J］.电机与控制学报，2009，13(4):576 －580.

LIU Luzhou，XIAO Jian，WANG Song.Identification of nice nonlinear model and its internal control［J］.Electric Machines and Control，2009，13(4):576 －580.

［14］ POLYCARPOU M M，IOANNOU P A.A robust adaptive nonlinear control design［J］.Automatica，1996，32(3):423 －427.

［15］ SWAROOP D.Dynamic surface control for a class of nonlinear systems［J］.IEEE Transactions on Automatic Control，2000，45(10):1893－1899.

［16］ 梁勇，尚安利，邓方林.一类非线性系统的动态面二阶滑模控制［J］.系统工程与电子技术，2004，26(10):1468 －1470.

LIANG Yong，SHANG Anli，DENG Fanglin.Dynamic surface second－order sliding mode control for a class of nonlinear systems［J］.Systems Engineering and Electronics，2004，26(10):1468－1470.

［17］ 张天平，文慧.基于ISS的非线性纯反馈系统的自适应动态面控制［J］.控制与决策，2009，24(11):1702－1712.

ZHANG Tianping，WEN Hui.Adaptive dynamic surface control for nonlinear pure feedback systems via input-to-state stability［J］.Control and Decision，2009，24(11):1707－1712.

(编辑:张诗阁)

Dynamic surface output regulation method for a class of uncertain nonlinear systems

MENG Gui-zhi1，2MA Ke-mao1
(1.Control and Simulation Center，Harbin Institute of Technology，Harbin 150001，China;
2.Department of Applied Mathematics，Harbin University of Science and Technology，Harbin 150080，China)

For a class of nonlinear uncertain systems driven by a linear，neutrally stable exosystem，output regulation problem is considered with the existence of unmodeled dynamics and external disturbances.The dynamic surface method and internal model principle were utilized to propose a control design method.Based on necessary condition of output regulation problem for nonlinear systems，the output regulation problem was transformed to a stabilization problem by using state variable change and a canonical internal model.The dynamic surface method first introduced order filter into the backstepping design to cope with the problem of“explosion of the terms”in it.An internal equation with error was designed via exosystem information，and a robust control law was designed to stabilize the closed-loop system.Simulation results via exosystem information show that the control scheme ensures all signals to be bounded and the error signal to be within a desired range.

nonlinear systems;output regulation;internal model;backstepping design;dynamic surface control

TP 271

A

1007－449X(2011)05－0103－06

2010－12－13

国家自然科学基金(60736022)

孟桂芝(1979—)，女，博士研究生，讲师，研究方向为非线性控制;

马克茂(1970—)，男，博士，教授，博士生导师，研究方向为飞行器制导、控制，鲁棒控制，非线性控制等。