第二积分中值定理“中间点”的渐近性再分析

伍建华，孙霞林，熊德之

(武汉工程大学理学院智能机器人湖北省重点实验室，湖北武汉 430073)

第二积分中值定理“中间点”的渐近性再分析

伍建华，孙霞林，熊德之

(武汉工程大学理学院智能机器人湖北省重点实验室，湖北武汉 430073)

对于第二积分中值定理中的“中间点”的渐进性问题，将区间的端点推广到区间中的任意点，给出并证明了更一般的结论，改进和推广了现有的相关结论。

第二积分中值定理;中间点;渐近性

微积分中值定理，近年来有大量的文献对其进行探讨［1-8］，第二积分中值定理“中间点”问题，文献［1-2］给出了精彩的结论。但由于讨论都囿于左端点a，笔者将给出更一般的结果，将文献［1-2］的结果推广到区间的任意点，文献［1-2］的有关定理可以看成这个定理的一般推论。为叙述方便，将第二积分中值定理引述如下:

设g(x)在区间［a，b］上可积，则:

(ⅰ)若f(x)在区间［a，b］单减非负，存在ξ∈［a，b］使:

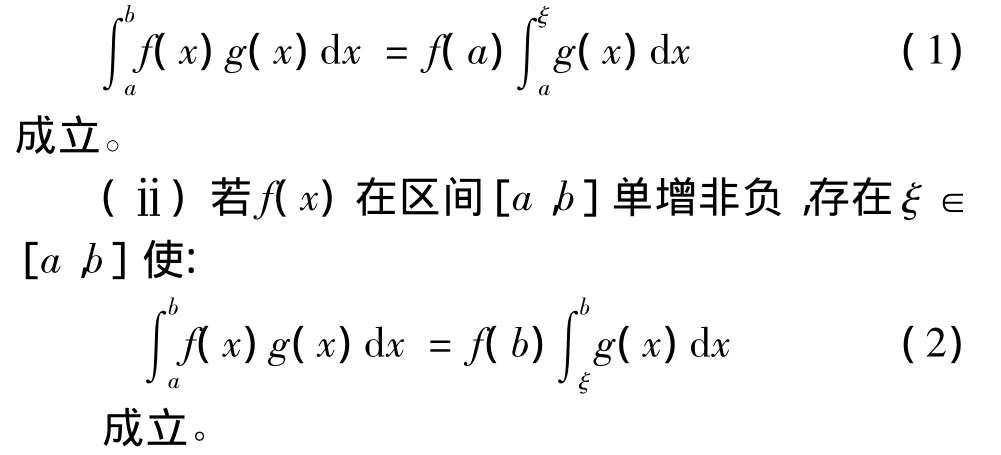
(ⅲ)若f(x)在区间［a，b］上单调时，存在ξ∈［a，b］使:

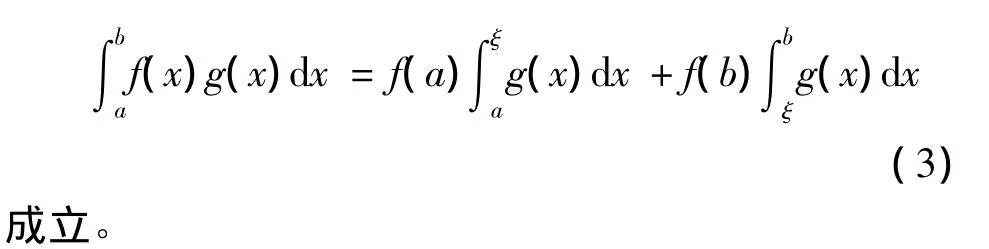
1 渐近性定理证明

引理1 设g(x)在［a，b］上可积，η是区间［a，b］中某一点，即a≤η≤b，且存在实数A，α ＞-1，使得:

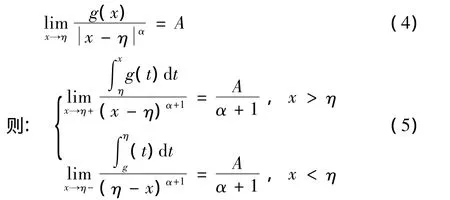
证明:当x＞η时，由文献［1］可知式(5)中第1个式子成立。当 x＜η时，由条件式(4)可知:∀ ε＞0，∃δ＞0，当x∈(η-δ，η)，有:(A-ε)(η -x)α＜ g(x)＜ (A+ ε)(η -x)α，类似文献［1］的证明，对式(5)从x到η的积分，可证式(5)中第2个式子也成立。

对于区间［a，b］中某一点η，即a≤η≤b，为了叙述的方便，在以下的证明中，a→ η，b→ η表示a→ η-，b→ η+。

引理2 设函数f(x)，g(x)在［a，b］上可积，η是区间［a，b］中某一点，即a≤η≤b，且存在实数A，B，P，α ≥-1，β≥-1，α + β ＞ -1，，使得:

引理3 设函数f(x)，g(x)在［a，b］上可积，η是区间［a，b］中某一点，即a≤η≤b，且存在实数A，B，P，Q，α ＞ -1，β ＞ -1，α + β ＞ -1，使得:

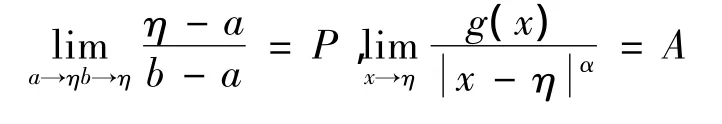
证明:1)当a＜η＜ξ≤b时，由积分第二中值定理式(1)及定理条件和引理1有:

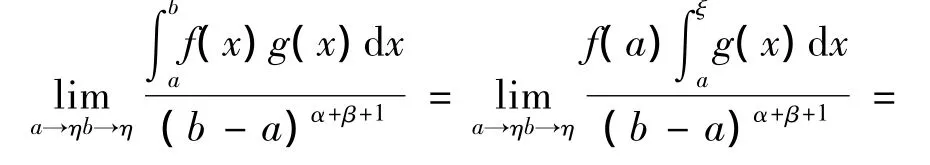
如果考虑趋向左端点的渐近性，则有下面的定理。

定理2 如果:

1)f(x)在区间［a，b］上单降非负，g(x)在区间［a，b］上是可积;

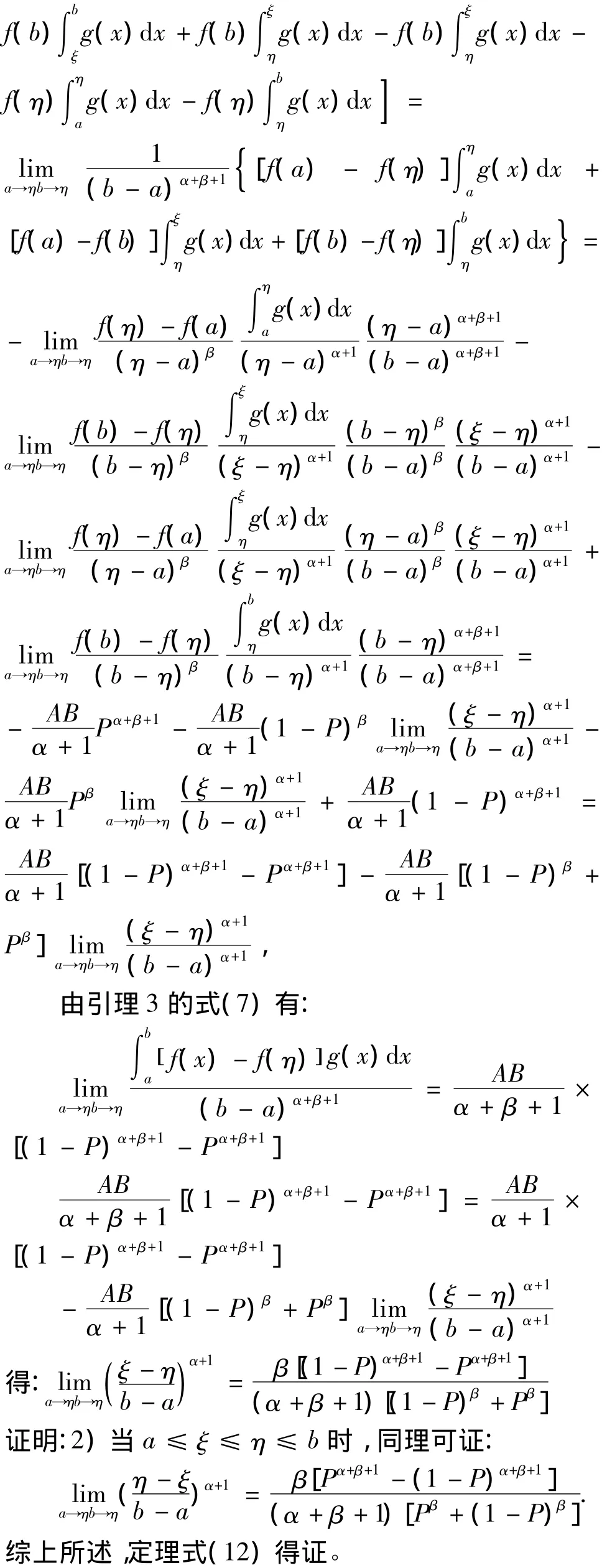
2 推 论

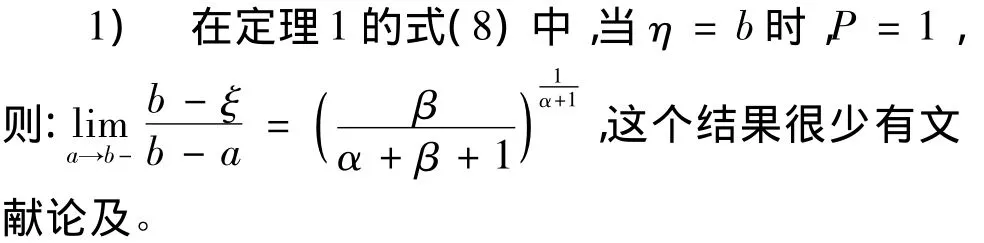
2) 在定理2的式(9)中，就是文献［1］的推论1，当α =0时，就是文献［2］的定理1。

文中的结论不仅推广了目前论述第二积分中值定理渐近性文献中的大部分结果，也给出了目前很少论及的趋向右端点的渐近性结论。

［1］刘文武.积分第二中值定理“中间点”的渐近性分析［J］.数学的实践与认识，2005，35(9):221-225.

LIU Wen-wu.Analysis on the asymptoticity of the intermediate point in the second mean value theorem for integrals［J］.Mathematics in Practice and Theory，2005，35(9):221-225.

［2］吴至友，夏雪.积分第二中值定理“中间点”的渐近性［J］.数学的实践与认识，2004，34(3):171-176.

WU Zhi-you，XIA Xue.On the second mean value theorem for integrals［J］.Mathematics in Practice and Theory，2004，34(3)，171-176.

［3］邹兆南，谭远顺.Cauchy微分中值定理的多种探究式证明法［J］.重庆交通大学学报:自然科学版，2009，28(5):976-978.

ZOU Zhao-nan，TAN Yuan—shun.Several exploration methods to prove the cauchy mean theorem［J］.Journal of Chongqing Jiaotong University:Natural Science，2009，28(5):976-978.

［4］Ricardo Almeida，An elementary proof Of a converse mean-value Theorem［J］.International Journal of Mathematical Education in Science and Technology，2008，39(8):1110-1111.

［5］Tong J and Braza P A.A converse of the mean value theorem［J］.Amer.Math.Monthly，1997 ，104(10):939-942.

［6］TONG Jing-cheng.Note the mean value theorems for differentials and integrals［J］.The Journal of the Elisha Mitchell Scientific Society，1998，114(4):225-226.

［7］伍建华.关于第二积分中值定理渐近性的一个注记［J］.武汉化工学院学报，2006，28(4):73-74.

WU Jian-hua.A note on asymptotic in second mean value theorem for integrals［J］.Journal of Wuhan Institute of Chemical Technology，2006，28(4):73-74.

［8］伍建华.第二积分中值定理中ξ的渐近性一般性证明［J］.高等数学研究，2006，9(4):30-31.

WU Jian-hua.The second integral mean-value theorem ξ asymptotic behavior of the general proof［J］.Studies in College Mathematics，2006，9(4):30-31.

Further Analysis on Asymptotic Behavior of Interior Point in Second Mean Value Theorem for Integration

WU Jian-hua，SUN Xia-lin，XIONG De-zhi
(School of Science，Wuhan Institute of Technology，Hubei Province Key Laboratory of Intelligent Robot，Wuhan 430205，Hubei，China)

As for asymptotic behavior of interior point in Second Mean Value Theorem for Integration，this article expands end points to any points in the interval，and draws a more generalized conclusion to improve and promote present related conclusions.

second mean value theorem for integration;interior point;asymptotic behavior

O172.2

A

1674-0696(2011)03-0514-05

2011-02-23;

2011-03-25

"十一五"国家课题(FIB070335-B2-04)

伍建华(1955-)，男，湖北黄石人，副教授，硕士，主要从事数学教学，算法分析方面的研究。E-mail:jhuawu@126.com。