基于Monte Carlo 法的山区路网应急中心选址
宋永朝,韩 伟,梁乃兴,潘晓东,焦建华
(1.重庆交通大学交通运输学院,重庆 400074;2.云南石锁高速公路有限公司,云南昆明 650217;3.重庆交通大学土木建筑学院,重庆 400074;4.同济大学交通运输工程学院,上海 201804;5.中交第一公路勘察设计院,陕西西安 710065)
基于Monte Carlo 法的山区路网应急中心选址
宋永朝1,韩 伟2,梁乃兴3,潘晓东4,焦建华5
(1.重庆交通大学交通运输学院,重庆 400074;2.云南石锁高速公路有限公司,云南昆明 650217;3.重庆交通大学土木建筑学院,重庆 400074;4.同济大学交通运输工程学院,上海 201804;5.中交第一公路勘察设计院,陕西西安 710065)
阐述了灾时山区路网各路段组成单元通行概率的分析方法,采用Monte Carlo模拟法对山区路网连通可靠度进行分析和计算,并通过概率解析法来检验Monte Carlo模拟法的计算精度。采用Monte Carlo模拟法分析路网节点间连通可靠度,提出了灾时山区路网应急救护中心优化选址方法。最后,通过实例阐述其计算过程。结果表明:采用Monte Carlo模拟法分析山区路网交通节点间的连通可靠度,找出灾时山区路网连通薄弱环节,为山区应急救护中心优化选址提供依据。
交通工程;蒙特卡罗;山区路网;连通可靠度;应急中心
中国是一个多山的国家,山区面积占国土总面积的70%。山区路网是山区防、救灾系统的重要组成部分。山区经济发展相对落后,路网连通性存在的问题加剧了灾害事件所造成的影响程度,如何改善山区路网连通性能,有效提高山区路网的抗灾、备灾能力,凸显其重要性。
日本学者Mine和Kawai[1]1982年首次提出了连通可靠度的概念,Fratta和 Montanari[2]采用布尔代数方法求解路径集割集来计算路网连通可靠度。国内相关究起步相对比较晚,主要集中在灾害交通系统的抗震可靠性方面,提出了灾害下交通网络的连通概率预测模型[3-7]。笔者以山区路网为研究对象,运用Monte Carlo模拟法,分析山区路网的连通可靠性能,为山区应急救护中心选址提供依据。
1 山区路网连通可靠性
连通可靠性也称为连通可靠度,是路网可靠性一项评价指标,用于评价灾害条件下路网任意两节间的连通程度,以判断路网承受灾害的能力。山区路网是一个复杂网络系统,山区路网连通可靠度反映的是山区交通网络节点之间保持连通的概率。
在探讨灾时山区道路交通可靠性研究过程中,需要考虑2个方面的因素来确定其道路的通行概率:一个因素是道路(路基路面、桥梁、边坡、隧道)的抗灾能力;另一个因素是道路两侧受沿线建筑物倒塌造成的瓦砾阻塞量的影响。道路的连通概率Pc由式(1)得:

式中:Pst为路段沿线建筑物倒塌的通行概率;Ptr为道路通行概率。若道路不受其中某一因素影响时,只需将其通行概率设为1即可。
道路通常由路段、桥梁、边坡、隧道等单元组成,相当于路段单元和桥梁(或者边坡、隧道)单元的串联。其中之一破坏则该道路就破坏,故整个道路连通概率Ptr等于路段单元通行概率Pr与桥梁(或者边坡、隧道)单元通行概率Pb之积。道路连通概率Ptr由式(2)得:

式中:Pb为桥梁单元的通行概率;Ps为边坡单元的通行概率;Pt为隧道单元的通行概率。若道路中不包含某单元,只需将其通行概率设为1即可。
关于灾害下沿线建筑物倒塌的通行概率预测模型及路段、桥梁、边坡、隧道的通行概率预测已展开了相关研究。宋建学,等[3]则提出了道路沿线建筑物灾后倒塌瓦砾阻塞量预测模型;李英民,等[7]综合了山区道路、建筑物特点,对模型予以了修正;姜淑珍,等[4]采用模糊易损性分析方法,确定了各震害因子的分类情况及对应的量化值;朱美珍,等[5]根据桥梁样本资料及震害经验,建立了公路桥梁震害的非线性预测经验公式;王余庆,等[6]综合考虑地质、地貌、地震、降雨等影响因子,确定了边坡单元通行概率;李英民,等[7]通过采用模糊层次综合评估法来预测隧道震后破坏程度。
2 山区路网连通可靠度计算
灾害事件下交通网络的连通可靠性分析方法归纳起来分为2类:概率解析方法与随机模拟方法。其中,Monte Carlo模拟法属于随机模拟方法,适用于大型复杂网络的连通可靠度计算。
2.1 Monte Carlo基本方法
Monte Carl模拟法实质是采用随机抽样的频率作为几率的近似值,当样品量足够大时,则频率就是概率[8];Monte Carlo模拟法是利用网络各单元破坏状态,通过计算源点与汇点处于连通状态的频率,以似频的破坏概率进行随机模拟,近似再现网络各单元的率计算代替精确概率分析,计算流程如图1。
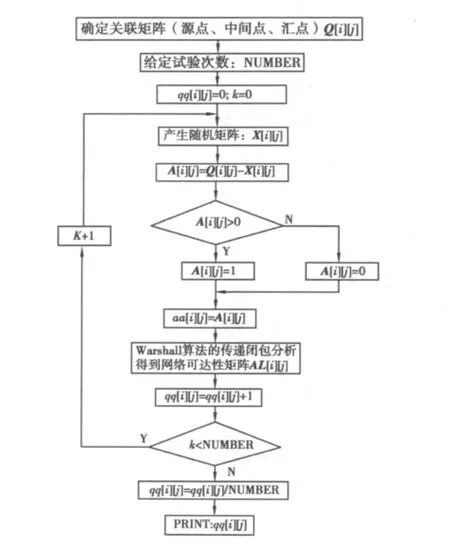
图1 Monte Carlo模拟法计算流程Fig.1 Calculation process of Monte Carlo simulation
2.2 Monte Carlo模拟法精度分析
以船形网络图(图2)为例,分析Monte Carlo模拟法的计算精度。设所有元件的可靠度(各路段的连通概率)都是0.5,节点的可靠度设为1.0,建立关联矩阵 Q[i][j]。

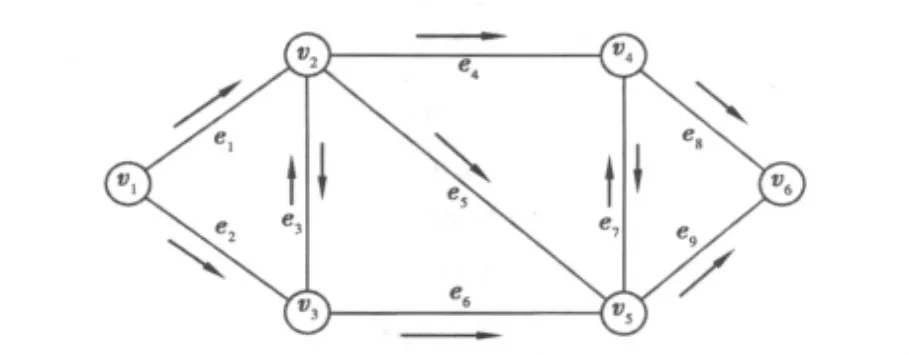
图2 船形网络Fig.2 Network liking boat
运用概率解析法对船形网络的连通概率进行计算[9],得出连通可靠度的精确值 R[i][j]。

采用Monte Carlo模拟法对船形网络图连通概率进行随机模拟,模拟次数为1 000,10 000,100 000次,得出的结果分别为 M1000,M10000,M100000。

模拟次数为1 000,10 000,100 000的各节点连通可靠度值与精确值R[i][j]进行比对分析,其相对误差如图3。
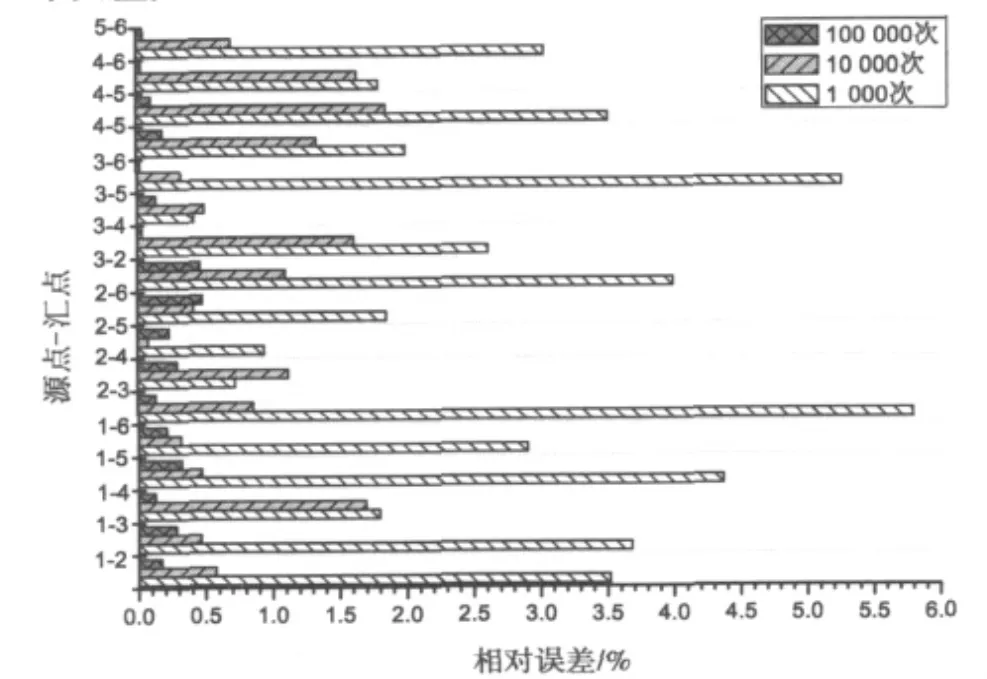
图3 Monte Carlo模拟计算误差Fig.3 Calculation error of Monte Carlo simulation
从图3中可知:模拟次数1 000次的相对误差在5%左右;模拟次数10 000次时,相对误差低于2%;模拟次数达100 000次时,计算结果的相对误差在0.5%以下。由此可见,采用Monte Carlo模拟法计算交通网络连通可靠度,可以满足其精度要求。
3 交通网络应急救护中心选址
1)在不考虑交通节点重要性差异情况下,在交通网络中的某交叉口处设置应急救护中心,分析在该路网中所选位置是否为应急救护中心的最佳选址位置。
2)利用Monte Carlo模拟法进行计算,分别以各个交叉路口作为应急救护中心的情况下,计算出该交叉路口到路网中其他节点的连通概率。然后分析出某交叉口为应急救护中心时,对整个系统在灾后救护、运送救灾物资时的效果最好,即可确定该处为应急救护中心的最佳选址位置。应急救护中心的选址优化步骤如下:
①分别假定各个交叉路口为应急救护中心,进行Monte Carlo模拟分析,计算出该交叉路口到路网中其他节点的连通概率。
②求解出以每个交叉路口为救护中心时,各个交叉路口j的连通可靠度的平均值Xj:
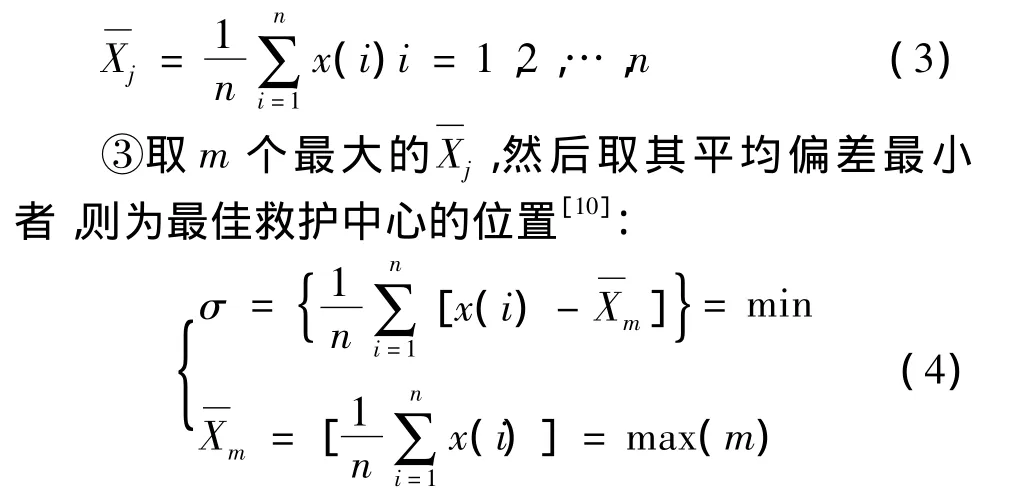
4 算例
笔者选用重庆某山区路网进行分析,路网结构如图4,路网中包含50条边,37个节点。其中,该路网的拓扑结构及其路段连通概率[11]如表1(地震设防等级以烈度为7度计)。
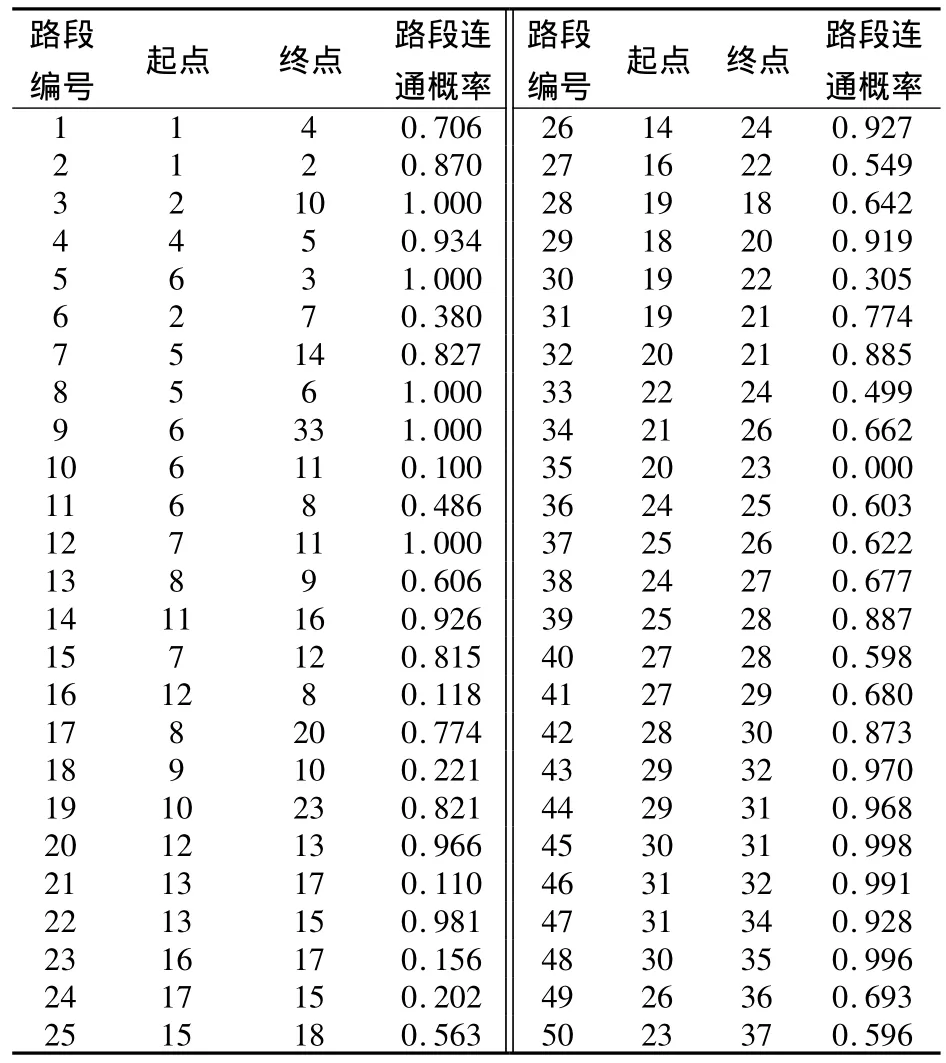
表1 某山区路网各路段连通概率Tab.1 Connectivity probability of the mountainous road network
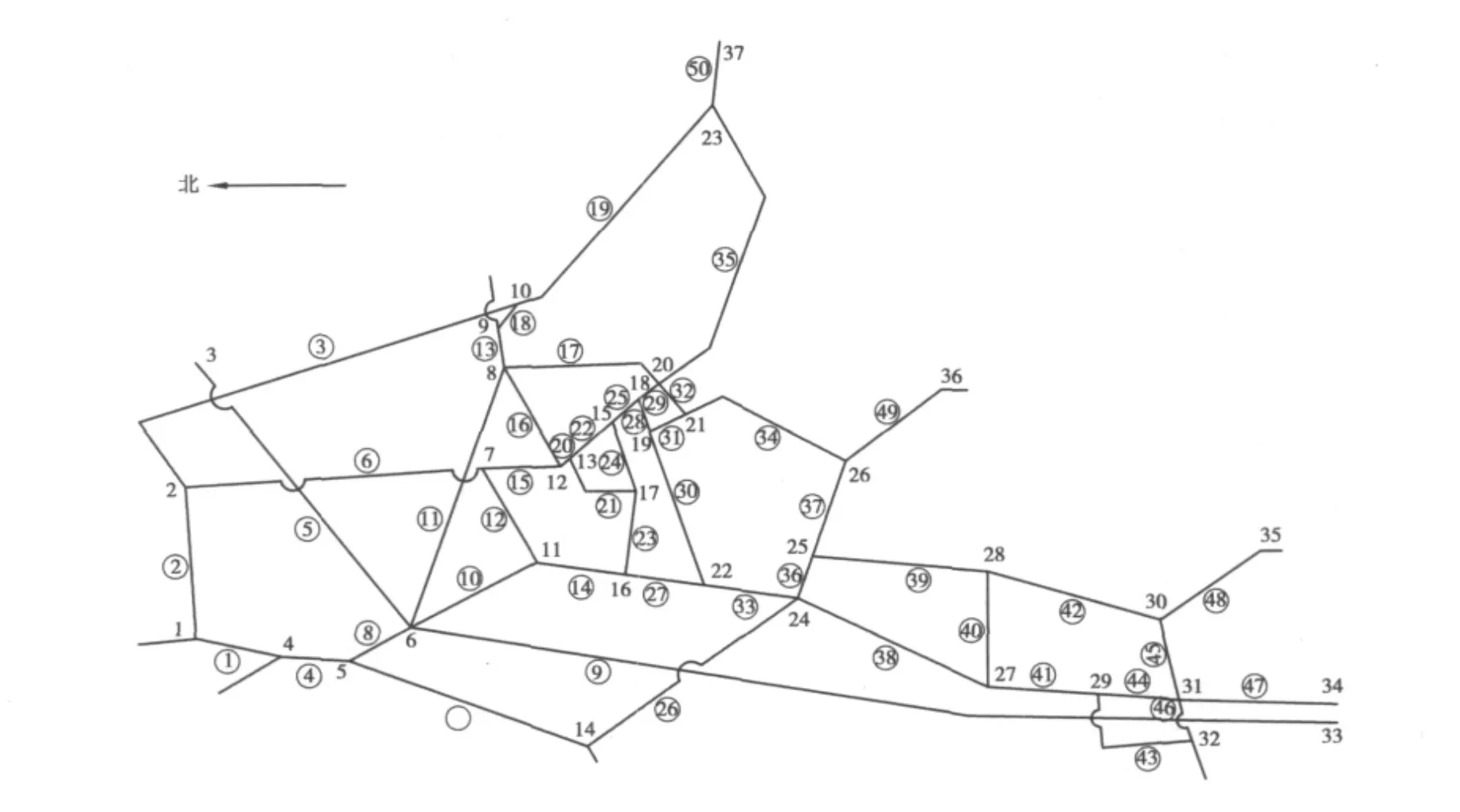
图4 某山区路网结构Fig.4 Topological structure of the mountainous road network
根据路网结构图以及网络节点之间的拓扑关系,运用Monte Carlo模拟法得出交通网络中各点之间的连通可靠度。连通等级判定方法[12]为:连通可靠度大于0.8,连通等级定为可靠;连通可靠度在0.4~0.8之间,连通等级定为中等可靠;连通可靠度小于0.4,连通等级定为严重不可靠等级。以1节点为例,运用Monte Carlo模拟法分析1节点到路网中其它各节点的连通可靠度,计算结果如表2。
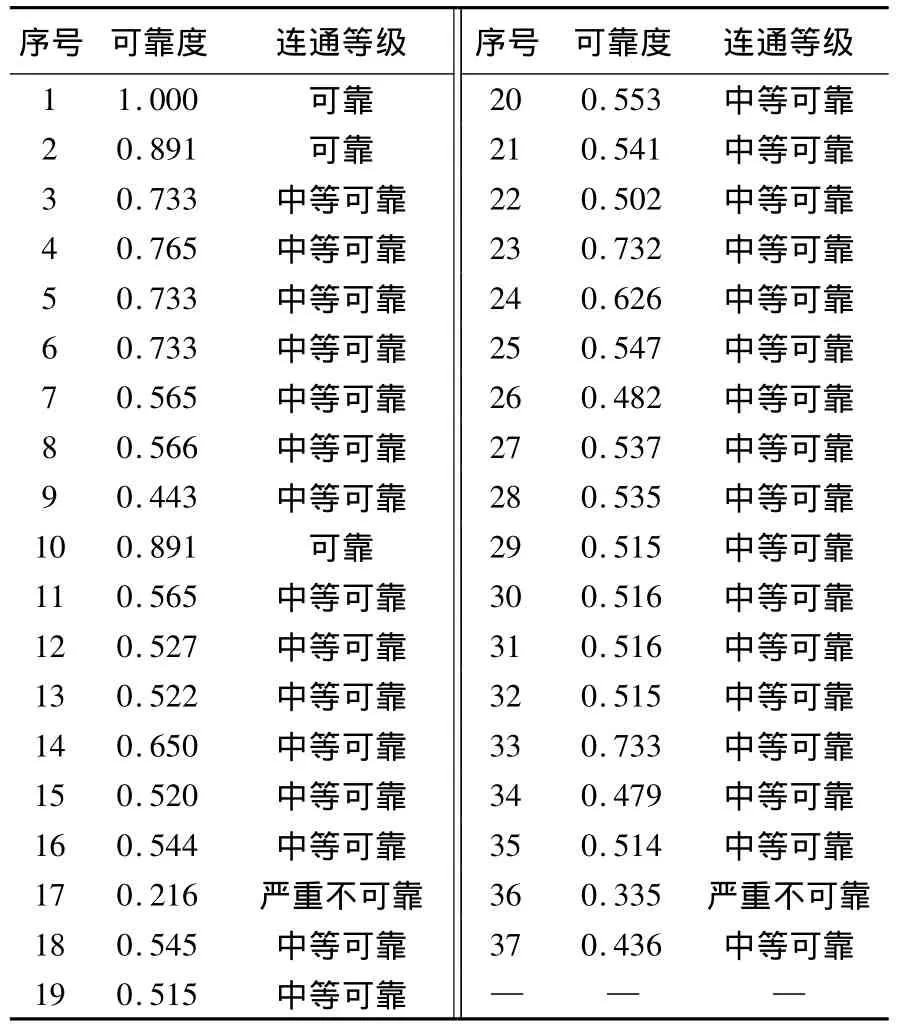
表2 1节点到其他各节点间的连通可靠度Tab.2 Connectivity reliability of edges between nodes
假定在11节点位置设为应急救护中心,运用Monte Carlo模拟算法,得出11节点到路网中其它各节点的连通可靠度,计算结果如表3。
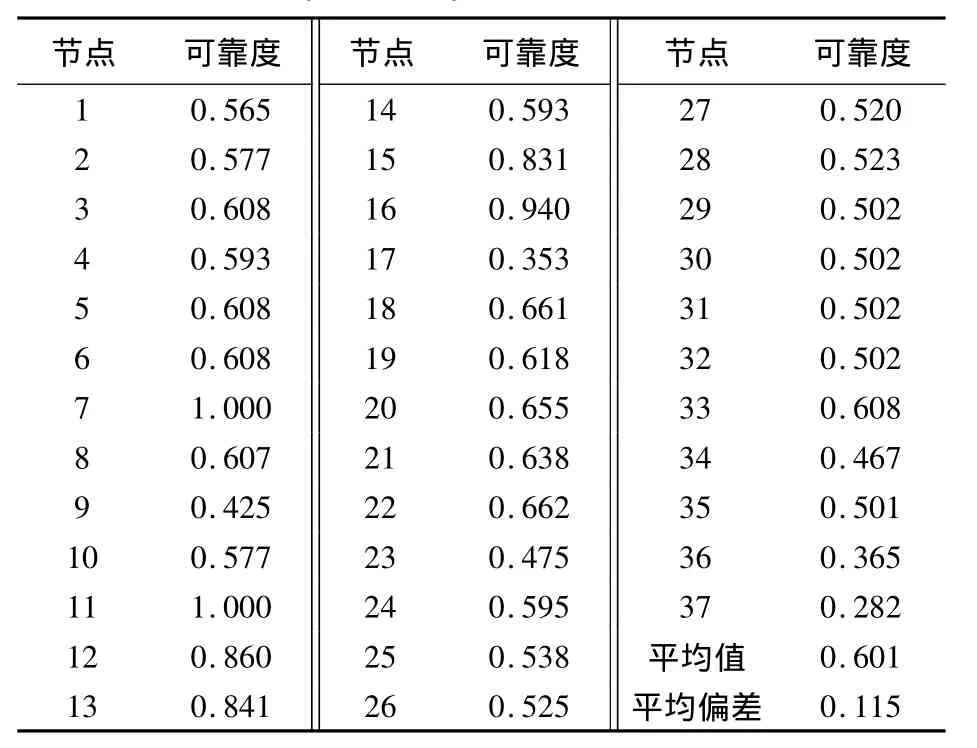
表3 11节点到其他各节点间的连通可靠度Tab.3 Connectivity reliability between node 11 and other nodes
分别以每个节点为源点,采用Monte Carlo模拟法计算出该交叉路口到路网中其他节点的连通概率,根据评判方法,可得出最佳的救护中心位置为24节点,24节点到其它各节点的连通可靠度如表4。
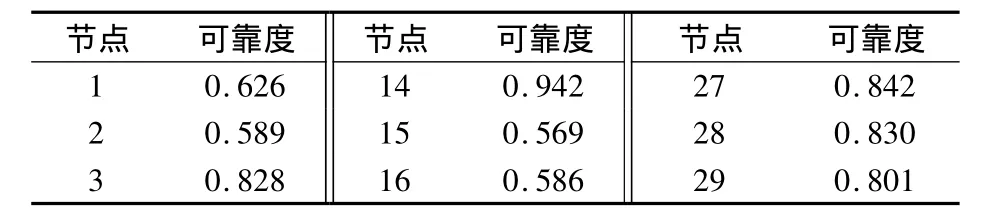
表4 24节点到其他各节点间的连通可靠度Tab.4 Connectivity reliability between node 24 and other nodes

(续表4)
若路网中11、24节点的2个应急救护中心同时存在时,计算应急救护中心(11、24节点)到达路网中其他节点的连通可靠度,得出该路网中各节点与应急救护中心之间的连通可靠度计算值,各节点的连通可靠度如表5。
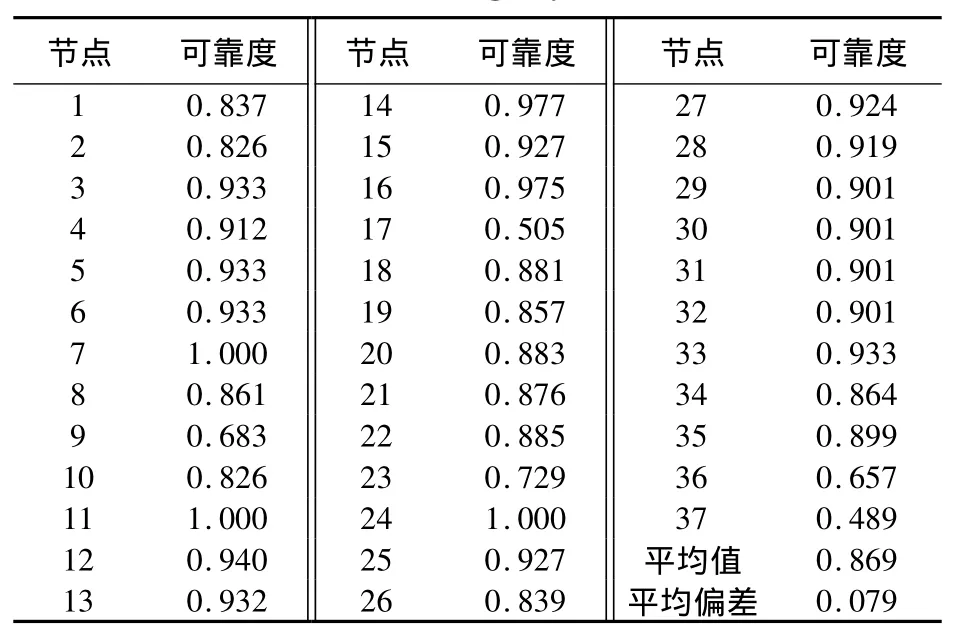
表5 11、24节点为应急救护中心的各节点连通可靠度Tab.5 Connectivity reliability between nodes while node 11 and node 24 as emergency rescue center
表4(24节点为应急救护中心)、表5(11、24节点为应急救护中心)分别表示路网中设置为1个、2个应急救护中心时的节点连通可靠度计算值,比对表4、表5中的连通可靠度值大小可以看出,应急救护中心越多(若经费许可),各交通节点与应急救护中心间的连通性越好。
5 结语
1)山区路网连通可靠度取决于路段、桥梁、边坡、隧道的抗灾能力以及沿线建筑物倒塌的瓦砾阻塞量的影响,路段单元通行概率与桥梁、边坡、隧道等单元通行概率之积即为整个道路的连通概率。
2)分析了Monte Carlo模拟法的基本原理及计算过程,运用概率解析法来检验Monte Carlo模拟法的计算精度。
3)运用Monte Carlo模拟法对山区路网交通节点进行连通可靠度分析,提出了山区应急救护中心的优化选址方法,并通过实例阐述其计算过程,可为山区应急救护中心选址提供依据。
[1]Mine H,Kawai H.Mathematics for reliability analysis[M].Tokyo:Asakura-shorten,1982.
[2]Fratta L,Montanari U G.A boolean algebra method for computing the terminal reliability in a communication network[J].IEEE Trans.Circuit Theory,1973,20(3):203-211.
[3]宋建学,李杰.震后城市交通系统连通性模拟[J].自然灾害学报,1996,5(1):73-78.
SONG Jian-xue,LI Jie.Simulation on accessibility of postearthquake urban transportation system[J].Journal of Natural Disasters,1996,5(1):73-78.
[4]姜淑珍,柳春光.三亚市交通系统易损性分析[J].世界地震工程,2005,21(3):23-27.
JIANG Shu-zhen,LIU Chun-guang.Vulnerability analysis of transportation system in Sanya[J].World Earthquake Engineering,2005,21(3):23-27.
[5]朱美珍.公路桥梁的震害预测的实用方法[J].同济大学学报,1994,22(3):21-26.
ZHU Mei-zhen.A practical method for predicting seismic damage of highway bridges[J].Journal of Tongji University,1994,22(3):21-26.
[6]王余庆,辛鸿博,高艳平,等.预测岩土边坡地震崩滑的综合指标法研究[J].岩土工程学报,2001,23(3):311-314.
WANG Yu-qing,XIN Hong-bo,GAO Yan-ping,et al.Study on comprehensive index method for predicting earthquake-induced landslides[J].Chinese Journal of Geotechnical Engineering,2001,23(3):311-314.
[7]李英民,王丽萍,刘立平.山地城市交通系统震害预测模型及其应用[J].西南交通大学学报,2009,44(2):171-176.
LI Ying-min,WANG Li-ping,LIU Li-ping.Predictive model for seismic damage of transportation system in mountain cities and its application[J].Journal of Southwest Jiaotong University,2009,44(2):171-176.
[8]Meguro K,Hakuno M.Simulation of collapse of structure due to earthquake using the extended distinct element method[J].Proceedings of Tenth World Conference on Earthquake Engineering,1992(7):3793-3796.
[9]金国梁.生命线工程网络震害预测方法讨论[J].工程抗震,1994,12(4):32-36.
JIN Guo-liang.Discussion of network seismic damage prediction methods for lifeline projects[J].Antiseismic Engineering,1994,12(4):32-36.
[10]柳春光,杜玮,瞿桐.城市交通系统抗震可靠性研究[J].地震工程与工程振动,1999,19(2):95-99.
LIU Chun-guang,DU Wei,ZHAI Tong.Reliability analysis of urban transportation system[J].Earthquake Engineering and Engineering Vibration,1999,19(2):95-99.
[11]陶小林.山地城市交通系统震害预测及应用研究[D].重庆:重庆大学,2007.
Study on Location of Emergency Rescue Center for Mountainous Road Network Based on Monte Carlo Method
SONG Yong-chao1,HAN Wei2,LIANG Nai-xing3,PAN Xiao-dong4,JIAO Jian-hua5
(1.School of Transportation Engineering,Chongqing Jiaotong University,Chongqing 400074,China;
2.Yunnan Shisuo Expressway Co.,Ltd.,Kunming 650217,Yunnan,China;
3.School of Civil Engineering and Architecture,Chongqing Jiaotong University,Chongqing 400074,China;
4.School of Transportation Engineering Tongji University,Shanghai 201804 ,China;
5.First Highway Consultants Co.,Ltd.,(FHCC),Xi'an 710065,Shaanxi,China)
Some analysis methods for the access probability of the mountainous road network component units were illuminated when disasters occurred.Monte Carlo simulation was applied to analyzing and calculating mountainous road network connectivity reliability.The calculation precision of Monte Carlo simulation was tested by probability analytic method.A optimization means for selecting the location of the emergency rescue center was provided by Monte Carlo simulation.Finally,calculated process was illustrated through numerical example.Results showed that some weak links of mountainous road network for connectivity could be obtained by Monte Carlo simulation.Selecting the optimum location for the emergency rescue center was of significance when disasters occurred.
traffic engineering;Monte Carlo;mountainous road network;connectivity reliability;emergency rescue center
U491.13
A
1674-0696(2011)03-0424-05
2011-01-10;
2011-03-22
国家高技术研究发展计划(863计划)资助项目(2009AA11Z220);交通运输部西部交通建设科技资助项目(20043182233308)
宋永朝(1975-),男,湖南双峰人,讲师,博士,主要从事道路与交通工程方面研究。E-mail:songyc69@163.com。

