土石混填路基压实度波动计算模型研究
刘长发,赵明阶,汪 魁
(重庆交通大学 河海学院,重庆 400074)
土石混填路基压实度波动计算模型研究
刘长发,赵明阶,汪 魁
(重庆交通大学 河海学院,重庆 400074)
为实现土石混填路基压实质量准确、快速检测,基于土石复合介质波动传播特性,导出了通过纵横波速综合反演土石混填路基压实度的波动计算模型。并以瞬态瑞雷波测试为手段对模型路基进行现场波动测试,采集波动数据,计算路基压实度。最后将压实度理论计算值与灌砂法测试结果作对比分析,验证该模型的可靠性。
压实度;土石复合介质;瞬态瑞利波;灌砂法
压实度是路基压实质量评价的一个重要指标,它关系着路基的强度与稳定性,影响着路面的使用性能和使用寿命,因此压实度检测是路基施工质量控制的一个重要环节[1]。但是,目前常规的压实度检测方法还存在一定的不足,尤其是土石混填路基压实度的检测。常规的路基压实度检测方法仅适用于填筑集料粒径小,厚度较薄的土质路基,对于集料粒径变化大,含水量不均匀的土石复合介质路基却有相当大的局限性。
土石复合介质是典型的多相介质,由土颗粒、岩石颗粒、颗粒间的孔隙以及孔隙中的气体和水等部分组成,其动力响应是众多技术领域内一直备受关注的研究内容[2-3]。在岩土工程中,通过研究应力波在介质中的传播来间接解决土石复合路基的强度承载力及稳定性等问题,通过土石复合路基的波速测试评价其强度和压实度,其波速越高,波能量越强,路基的强度和压实度就越大[4-5]。实验研究也表明波在土石复合介质中的传播速度随含水量和孔隙度的降低而增大[6]。但是,目前路基压实质量检测广泛采用波速评价的方法仍处于定性层面,还不能解决土石混填路基的现场无扰动测试与远距离监控。其原因在于缺乏一个具有普遍意义的物性参数波动反演模型。
对于这个问题,文献[7]从多相体的角度出发,以弹性波作为手段,在宏观上采用等效连续介质理论,在微观上以White气囊理论模型为基础,综合运用等效体模型、Gasman方程、颗粒接触理论等理论探讨和研究了土石复合介质波动特征的变化规律,推导了土石复合介质的波速理论公式,并建立了土石混填路基压实度波动测试的理论模型。但是,该模型包含土石复合介质填料的含水量,因而无法实现快速测试。鉴于此,笔者在分析土石复合介质波动传播特性的基础上,通过因素影响分析,推导了土石混填路基压实度的简化波动计算模型。并利用瞬态瑞雷波对路基进行现场波动测试,通过理论分析计算与传统灌砂法的测试结果相对比,验证该模型的可行性。
1 土石复合介质压实度公式推导
多相土石复合介质的等效剪切模量和等效体积模量可由式(1)、式(2)[7]表示:
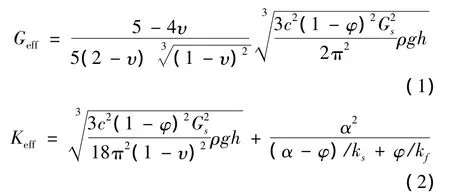
式中:Geff为土石多相复合介质的等效剪切模量;c为土石多相复合介质颗粒的平均接触点数;φ为土石多相复合介质孔隙度;υ为土石多相复合介质泊松比;h为土石介质的厚度;Gs为固体颗粒的剪切模量;ρ为土石多相复合介质密度;g为重力加速度;Keff为土石复合介质的等效体积模量;α为孔隙弹性系数;ks为固体相介质的等效体积模量;kf为土石复合介质液相的体积模量,kf可定义为[7]:kk
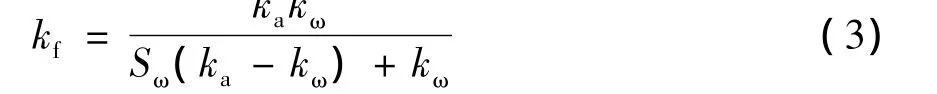
式中:Sω为土石复合介质的饱和度;ka,kω分别为气体液体的体积模量。
假设在宏观上将土石多相复合介质视为各向同性的弹性介质,则根据弹性波理论有土石多相复合介质的宏观弹性波传播速度[7]:

因为 ka< <ks,α-φ 在(-1,+1)范围内故式(6)可简化为:

式中:ω为含水率;ρω为水的密度,一般取为1;ρd为土石固体相等效密度(干密度);V为土石复合介质的总体积,取为单位1;Vv为土石复合介质的空隙体积;Vω为孔隙水的体积。
土石复合介质的密度可定义为[6]:

研究表明boit弹性系数与颗粒结构特征、孔隙压力、纵横向应力大小等因素有关[9];而颗粒结构特征及孔隙压力对土石复合介质波动传播特性影响较小[2]。鉴于路基分层填筑分层碾压的施工工艺,采用浅层波动测试,将boit弹性系数视为不变量。
土石复合介质泊松比可定义为[8]:

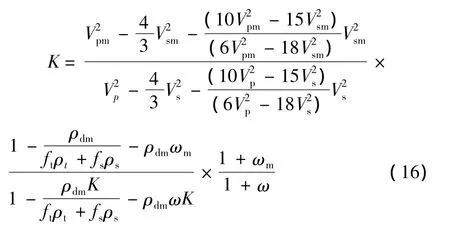
文献[6]对土石复合介质横波波速传播理论公式分析简化得到压实度的计算模型:

其中:F(υ)为泊松比的函数。
研究表明土石复合介质的波动传播特性主要受干密度、孔隙度、土石比和水饱度等的影响较大,而泊松比和粒径对其影响较小[2]。忽略泊松比对路基波动特性的影响,该模型可近似表达为:
1
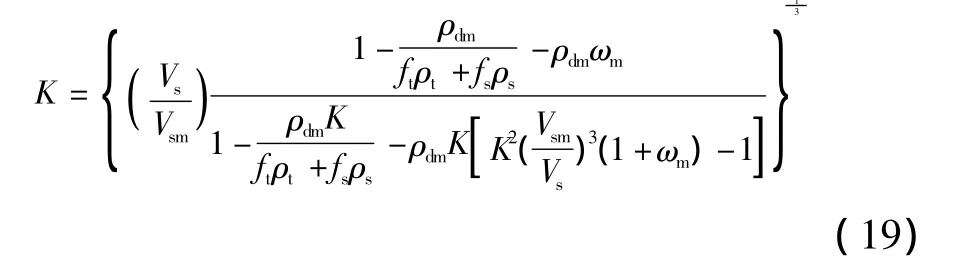
式(19)为土石复合介质压实度波动简化模型。
显然,该表达式为高阶隐式,存在多解情况。为了方便计算,建议采用枚举法进行编程计算。
2 实验验证
为了验证文中提出的土石混填路基波动简化模型的可行性,参考文献[10]和文献[11]利用瞬态瑞雷波法对实验模型路基进行现场波动测试。将本文推导的土石混填路基压实度波动简化计算模型(设为模型1)计算的压实度值与文献[3]推导的波动计算理论模型(设为模型2)的计算结果及灌砂法的测试结果对比,验证其可行性。
通过室内重型击实、波速测试及颗粒密度测试获得土石复合介质的物理指标:填料土体最大波速Vsmt=164 m/s,填料岩块的波速 Vsms=1 460 m/s,土样的最大干密度ρmdt=1 853 kg/m3,土样的最佳含水率ωmt=9.12%,以及土石颗粒的密度ρt=2 551 kg/m3,ρs=2 700 kg/m3。将实验数据带入下列3式:
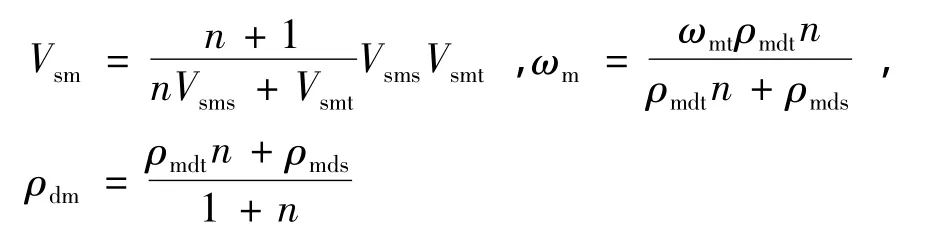
求得不同土石比混填路基在最密状态下的土石混填材料参数如表1。其中:n为土石比;Vsm,ωm,ρdm分别为土石混填材料最密实状态下的横波波速,含水率和干密度。
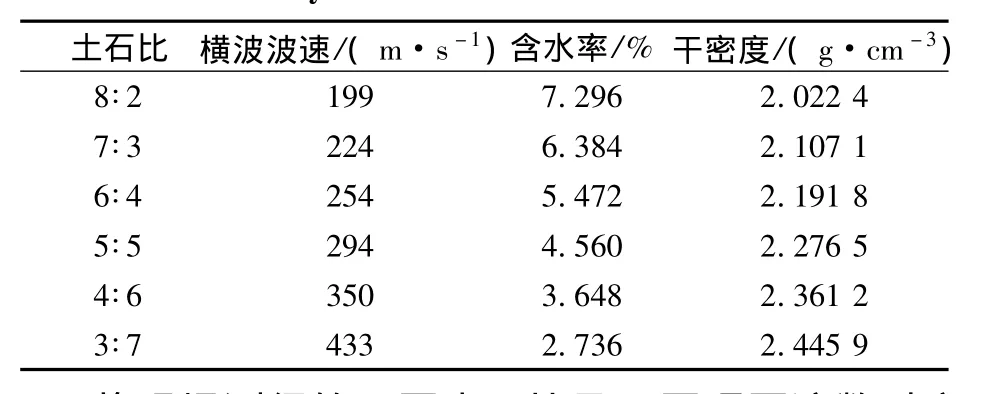
表1 土石混填材料参数Tab.1 Physical indexes of soil-stone mixture
将现场测得的不同土石比及不同碾压遍数对应的横波波速和其对应的土石混填材料参数带入模型1,可得不同土石比各不同碾压遍数下路基的压实度。将计算所得压实度绘制于图1(a)~图1(f),并与模型2计算值、灌砂法测试值作对比,验证其可靠性。
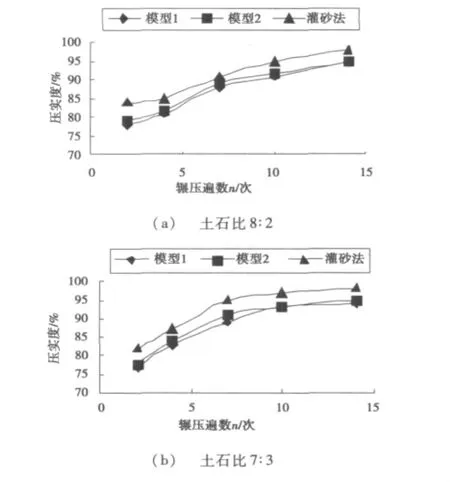
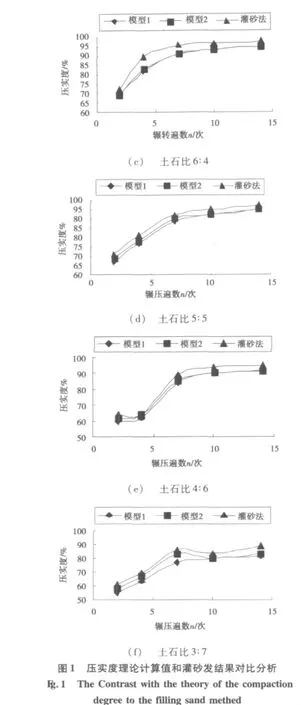
由图1(a)~图1(f)可以看出:土石混填路基压实度波动简化模型(模型1)的理论计算值除极个别值外,与文献[3]中模型(模型2)的理论计算值基本一致。但是波动模型的理论计算值普遍比灌砂法测试值偏低。研究分析认为波动测试的压实度是对路基压实效果的综合评价,具有平均的概念。而灌砂法测试的是某一个点的压实度,其代表性和可靠性由测区路基的含水量、孔隙体积和颗粒粒径大小的均匀性来决定。当这种不均匀性较大时,用灌砂法评价路基压实度就有很大的局限性和不合理性。因此,对于集料粒径变化大,含水量不均匀的土石混填路基波动测试压实度才是更加合理的检测方法。此外,值得指出的是当土石比较低,碾压遍数较少时,模型1计算的压实度值比模型2的理论计算值略微偏低1%~2%,而且随着土石比的降低这种偏差有增大的趋势。对于土石比较低的土石混填路基其土石颗粒形成的骨架孔隙较大,在碾压初期其泊松比变化较大。因此,当模型1忽略泊松比的变化带来的影响时,其会出现略微偏低的现象。当碾压遍数较多时,这种不一致性便降低,甚至消失,从而也佐证了该分析的正确性。综上所述,基于波动模型测试路基压实度更能真实反应路基的整体压实效果,更加有利于公路路基压实质量的检测和控制。
3 结语
笔者基于土石复合介质的波动传播特性推导了基于纵波波速、横波波速的土石混填路基压实度的简化波动反演模型,通过瞬态瑞利波进行现场波动测试,利用推导的理论公式进行压实度计算,并和传统的灌砂法结果进行对比。
1)对比分析表明:尽管本文在推导土石混填路基压实度纵横波速综合反演模型和其波动简化模型时采用了大量的近似处理,但其计算结果与文献[3]模型计算结果基本一致,说明该模型是可行的。
2)在室内试验测得土石填料的物理力学参数的基础上,通过建立土石混填路基压实度的横波波速、纵波波速的综合反演模型和其波动简化模型,可以利用瞬态瑞利波采集现场路基的波动参数,从而快速反演路基压实度,表明对土石混填路基压实度的无扰动测试与远距离监控是可行的。
3)计算结果分析表明:当采用低土石比进行路基填筑时,其土石颗粒形成的骨架孔隙较大,在碾压遍数较少时,路基横纵向变形差异较大,泊松比变化较大。此时,采用模型1计算的路基压实度值较模型2偏低1%~2%。随着碾压遍数的增加,这种差异性会减小消失,2种模型的计算结果也几乎一致。
最后,值得指出的是在公式推导过程中作了大量的近似处理,要获得更精确的计算模型还有待进一步的深入研究。
[1] 智胜英.直达波法检测路基压实度[D].天津:河北工业大学,2005.
[2]赵明阶,吕卫兵.土石多相复合介质的波动传播特性研究[J].岩石力学与工程学报,2005,24(增刊1):4917-4923.
ZHAO Ming-jie,LV Wei-bing.Properties of wave propagation in soil-stone composite medium[J].Journal of Rock Mechanics and Engineering,2005,24(supp1):4917-4923.
[3]刘颖,刘凯欣.横观各向同性含液饱和多孔介质中应力波传播的特征分析[J].应用数学与力学,2004,25(6):599-607.
LIU Ying,LIU Kai-xin.Characteristic analysis for stress wave propagation in transversely isotropic fluid-saturated porous media[J].Applied Mathematics and Mechanics,2004,25(6):599-607.
[4]范云.填土压实质量检测技术的发展与评析[J].岩石力学,2002,23(4):524-530.
FAN Yun.Advance and evaluation of checking technique on the quality of filled soil evaluation[J].Rock and Soil Mechanics,2002,23(4):524-530.
[5]顾汉明,宋先海,刘江平.用瞬态瑞雷波反演横波速度评价高速公路压碾效果[J].地质科技情报,2001(2):100-103.
GU Han-ming,SONG Xian-hai,LIU Jiang-ping.Evalution of the effect of compaction highway surface using shear velocity inversed by instantaneous rayleigh wave[J].Journal of Geological Science and Technology Information,2001(2):100-103.
[6]赵明阶.根据波速计算多相土石复合介质地基压实度的理论模型[J].水利学报,2007,38(5):618-623.
ZHAO Ming-jie.Theoretical model for calculating compactness of soil-stone mixture foundation according to wave propagation velocity[J].Journal of Hydraulic Engineering,2007,38(5):618-623.
[7]赵明阶,黄卫东,韦刚.公路土石混填路基压实度波动检测技术及应用[M].北京:人民交通出版社,2006.
[8]申卫兵,张保平.不同媒阶煤岩力学参数测试[J].岩石力学与工程学报,2000,19(增刊 1):860-862.
SEN Wei-bing,ZHANG Bao-ping.Testing study on mechanical parameters of coal[J].Journal of Rock Mechanic and Engineering,2000,19(supp1):860-862.
[9]吴世明,唐有职,陈龙珠.岩土工程波动勘测技术[M].北京:水利水电出版社,1992.
[10]韦刚,赵明阶,黄卫东.土石地基模型试验及压实度的波动检测[J].重庆交通学院学报,2004,23(4):49-53.
WEI Gang,ZHAO Ming-jie,HUANG Wei-dong.Soil-stone embankment models and wave testing compaction degree[J].Journal of Chongqing Jiaotong University,2004,23(4):49-53.
[11]阎学文,许安,任征.瞬态锤击测试土压实度的初步试验研究[J].筑路机械与施工机械化杂志,2007(1):60-62.
YAN Xue-wen,XU An,REN Zheng.Experimental research of soil compaction measure using transit hammer[J].Compaction Machinery& Construction Technology,2007(1):60-62.
Calculation Model for Soil-stone Mixture Foundation,s Compaction Degree according to Wave Propagation Velocity
LIU Chang-fa,ZHAO Ming-jie,WANG Kui
(School of River & Ocean Engineering,Chongqing Jiaotong University,Chongqing 400074,China)
In order to achieve the evaluation of the soil-stone mixture embankments,compaction more accurately more rapidly,the volatility model which could be used to calculate the compaction degree with the shear wave velocity and the longitudinal wave velocity was deduced according to the wave propagation characteristics of the soil-stone media.Then the Rayleigh wave testing is taken to collect the wave-data to calculate the embankments,compaction degree.Finally,contrast with the result of the filling sand method to verify its reliability.
compaction degree;soil-stone mixture;Rayleigh wave testing;filling sand method
U416.1
A
1674-0696(2011)03-0415-04
2010-11-15;
2011-04-18
刘长发(1986-),男,重庆梁平人,硕士研究生,主要从事波动检测技术方面的研究工作。E-mail:15823226951@qq.com。

