模块化免疫神经网络平衡模型的研究
侯家利
(东莞理工学院 计算机学院,东莞 523808)
0 引言
目前虽然已有多种网络安全的解决方案,如防火墙,入侵检测、容侵技术等技术,但是,网络安全问题还是不能被彻底解决。随着研究与应用的逐渐深入,人们已经意识到,利用传统的网络安全理论和技术,要想构造绝对安全的网络系统,在现实中几乎是不可能实现的梦想。因此,寻求新的网络安全理论和新的安全技术势在必行。
免疫网络学说认为当新的抗原进入机体,原有的安全平衡被打破,这样将激活机体内的免疫网络系统,使机体自我修复,再次达到新的网络安全平衡状态。[1,2]
利用免疫系统和遗传算法方面的理论构造了网络安全平衡器,为解决网络安全问题提供了一个新的途径,但平衡器检测模型中作用规则是抽象的函数和向量集,应用中还必须给予具体的实现。
1 网络安全平衡态
定义1 模块化平衡基是网络处理安全平衡最原始的向量集A1,A2,……, Am(其构成如公式1所示),不同的模块其向量集不同。
定义2 安全平衡态是安全的量化状态,是对网络遭受威胁后重新达到平衡的量化衡量。
定义3 策略Ai和适应度函数G(X)分别作用抗原,作用所得的值如超过平衡阈值,即:
≥ F (b1j1,b2j2,…,bmjm) =ij,1 ≤ j1≤ t1;1≤ j2≤ t2;……;1≤jm≤ tm,则称网络处于i类可疑不平衡态,而ij≥j,则称网络处于i类可疑平衡态。
利用下列竟争算法确定抗原处理单元:

其中:lk是新抗原的浓度,mk是不同处理单元中最优抗原浓度(安全平衡时的抗原浓度),是处理单元抗原的浓度域,分别是希尔函数。
选取Ui(0,1)和浓度域 值最接近的处理单元,这样可确定该处理单元的安全阈值、参数 α 和 k,是向量集 b,b,…,bii1j12j2mjm所对应的抗原与抗体的促进和抑制的希尔函数值。
不同的处理单元平衡不同的网络资源(抗原)。
2 网络安全平衡器
2.1 模块化平衡基
不同特性的抗原激活不同的处理单元,不同的处理单元对应不同基集,竞争算法可正确选取处理单元。[3]在选取之前对抗原进行分类,同时计算出抗原的浓度和抗体的浓度。
假设策略集A1,A2,…Am分别为:




其中,N为抗原(或抗体)个数,j是系统向量基集:{a11,a12,……,alkl}所对应的相关安全阈值。[4-5]
利用公式(2)计算抗原浓度x1。


计算抗体1,2,…,k的亲和力,再利用浓度公式计算出抗体1,2,…,k的浓度x2。
因有多个不同的基集和各基集对应的性能换算函数G (X)不同,上述x1和x2是一个动态变化的量。
2.2 适应度函数
如何选择适应度函数G(X)是构造平衡态检测模型的关键,我们选用主分量方法构造G(X),设有 X = (X1 ,... ,Xp)′是一个 p维随机变量,有二阶矩,记µ = E(X), 。考虑它的线性变换:

如果要用Y1尽可能多地保留原始的X的信息,经典的办法是使Y1的方差尽可能大,这需要对线性变换的系数l1加限制,一般要求它是单位向量,即I1′I1=1。其它的各Yi也希望尽可能多地保留X的信息,但前面的Y1,…,Yi-1已保留的信息就不再保留,即要求Cov ( Yi, Yj) = 0 ,j = 1, ..., i-1,同时对li也有I1′I1=1的要求。在这样的条件下使 Var (Yi)最大。设协方差阵∑的特征值为λ1≥λ2 ≥ ≥λp ≥0,相应的单位特征向量分别为 a1,a2, ,ap(当特征根有重根时单位特征向量不唯一 )。这时X的第i个主成分为 , Yi=a′X,i= 1, ,p,且 Var (Yi) = λi。记

则A为正交阵,Y=A′X,Var (Y)=Λ。
为了减少变量的个数 ,希望前几个Yi就可以代表X的大部分信息。计算出:
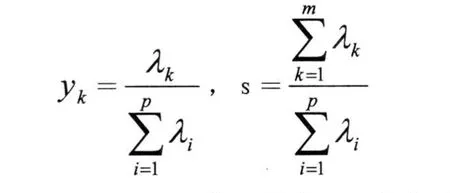
定义yk为主分量Yk的贡献率 ,s为主分量 Y1,…,Ym的累计贡献率。在上面的主分量计算方法中,方差越大的变量越被优先保留信息,实际中为了消除这种影响经常把变量标准化,即消除量纲和数量级对综合评价的影响。采用 ZScore方法进行标准化,即令:


相关阵R体现了各单目标之间的相关因素的影响程度,从而采取相应的措施,可以剔除重叠信息和体现单目标之间的相互影响。这时,主分量的协方差阵是Λ*=diag,),其中, ,为 R的特征根;根据R特征根λi相应的正交单位特征向量对X*做变换可以得出新的分量Y*i的表达式。*i作为第i个分量的方差;计算第个分量的贡献率:

对主分量进行综合可求得平衡态检测模型,由于Yi之间相互无关,可以采用加和形式:

3 平衡态检测模型
我们用x1代表抗原向量i的浓度,用x2代表抗体向量j的浓度,则所建模型如下:
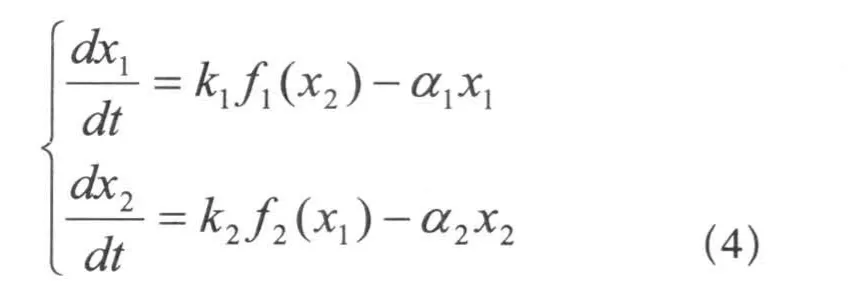
其中,参数αi 和ki (i=1,2)为正常数,f1(x2)和f2 (x1)为表达抑制(或促进)效应的Hill函数,满足下面条件:

第一方程描述了抗原浓度的演化过程,Hill函数f1(x2)描述了抗体对抗原输入率的抑制作用,参数αi(i=1,2)表示抗原的损失率, 由三部分组成:一部分来自免疫系统的清除, 一部分是因为转变为另一种表型, 第三部分是因为自然消亡。第二个方程描述了抗体的演化。抗体的输入率受抗原的抑制。
系统(6)的向量域为:

若选择m=[1,0],系统(6)是一个Km单调系统。从此向量域的形式可知,系统(6)是一个不可约矩阵,故系统(6)是一个不可约的Km单调系统。
4 平衡态平衡模型
用资源容量占有百分比的方差、资源被处理次数的方差的平均值来衡量,方差的数值越小则网络的平衡性能越好。
容量资源i占有百分比的方差:

其中:m表示资源i处理的业务总数,N表示第i类资源总数,Vsu[i]表示的是第 i 类资源被占用的容量,Vs[i]表示的是第i类资源的容量(i=1,2,…,N),Pl[i]表示的是单位时间内第 i 类资源被使用次数。
用平衡态检测模型判断资源平衡态,对于资源安全不平衡态,我们建立如下模型进行资源的安全平衡。
这里x1是第i类资源的供需浓度,pl是对于第i类资源的贡献率,pl第q类业务对第l类资源的消耗量,表示利用Hi计算出的关于第i类资源的供需浓度的标准供需指数,Hi是第i类资源的供需指数,n是系统总的资源数,qt表示间隔时间t内的有效资源的消耗度, 是第i类资源被使用的时间间隔量。因此,YEi是第i类资源平衡安全量。
H-H指数定义为某业务占有第i类资源的平方和。设Sj是业务j对资源i的占有百分比,n是第i类资源所处理的总业务数:

V是环境占用的统计变量,对于一定的业务数环境分享资源的变化量的增长导致H-H指数也随之增长。
适应度函数定义为:


5 结论
综合利用免疫系统和和遗传算法的相关机理构造了一个多层的、模块化的、动态的、自适应的、分布式的网络平衡器,首次提出了网络安全平衡的概念;建立了抗原与抗体平衡态检测的数学模型;安全平衡器通过表层检测进行处理分类,对于不安全态进行平衡判断,利用平衡态平衡模型使已受攻击的网络回归安全平衡状态,这为计算机安全环境的形成提供了良好的理论依据,为网络安全智能化提供了一个新的综合方案,理论证明方案是切实可行的。但应指出的是,由于首次提出网络安全平衡态,所以研究还有很多不完善的地方,下一步我们将讨论新抗体如何产生、各种阈值的确定以及平衡态平衡模型中各参数的规格化等内容。
[1] 张险锋,刘锦德.一种基于门限ECC的入侵容忍CA方案[J].计算机应用. 24(2): 5-8, 2004.
[2] 孙玉海,孟丽荣.基于多级入侵容忍的数据库安全解决方案[J].计算机工程与应用. 26(3):694-696, 2005.
[3] 侯家利,朱梅阶.模块化免疫神经网络的模型研究[J].电子学报.33(8):1502-1505,2005.
[4] Urbain J,Kanfman M,Thomas R.Towards a Logical Analysis of the Immune Response.Bull Math biol,1985,(114):527-561.
[5] Shannon CE. Communication theory of secrecy system.Bell System Technical Journal, 1949,28(10):656.715.
[6] Smith H L.System of ordinary differential equations which generate an order preserving flow,a survey of tesults.SIAM Rivew,1988,(30):87-113.
[7] Lou Jie,Ma Zhien,Shao Yiming,Han Litao.Modelling the interaction of T,antigen presenting cell and HIV1 in vivo.Computers&Mathematics with application,2004,(48):9-33.
[8] Eunju Jun a, Wonjoon Kim b, Soon Heung Chan. The analysis of security cost for different energy sources.Applied Energy, 2009 (86):1894–1901.

