我国经济增长因素的实证分析——基于索洛模型

丁 然

(浙江工商大学,杭州 310018)

经济增长,就是国民财富和社会财富的增长,即产出的增长,它表现为国民生产总值或国内生产总值或国民收入的增长。经济的持续增长,必将引起社会经济各方面的变化,具体反映在投入结构的变化、产出结构的变化和健康卫生状况及环境生态状况的变化等方面[1]。一般地说,持续、稳定而合理的经济增长,必将促成社会经济各方面的良性变化。正因如此,许多发展经济学家严格区分了“增长”和“发展”两个概念,把经济增长归为经济总量上的增长,而把经济发展看成是经济总量上的增长和结构变化[2]。事实上,如果研究的是长期增长问题,他总是与结构变化紧密相连的。没有投入要素总量、结构和质量的改变,要实现长期增长是不可能的。产出总量的增长总是伴随着各产业的兴衰而进行的,没有产出结构的变化,不可能实现长期的增长,收入与分配直接与各经济活动参与者的利益相关,经济的增长必然是正确的利益刺激的结果,没有收入分配的改善,经济的长期增长必然受到阻碍。

索洛对增长过程的经验研究,主要是关于各种生产要素对国民生产总值的贡献的经验评价,对经济学的发展具有特殊的贡献。索洛强调了技术进步在经济增长中的重要作用,为美国等西方国家致力于发展本国科学技术提供了直接的理论依据,对西方国家的科学技术政策实践和教育政策产生了巨大的积极影响。索洛在《技术变化与总生产函数》(1957)和《投资与技术进步》(1960)两文中的分析为后来发展为增长核算的研究手段奠定了基础。索洛通过计算相应的生产发展与以要素份额衡量的劳动和资本的供给发展之间的差额测定了生产技术在时间上的连续变化,接着他利用这些概算序列估计出生产函数,即产出与生产要素投入之间的数量关系[3]。

一、模型假设

20世纪30年代由数学家柯布(C.W.Cobb)和经济学家道格拉斯(PaulH.Douglas)提出的生产函数是现代经济增长实证分析的基础。其格式如下:

其中,Y代表经济总量,K代表资本投入量,L代表劳动投入量,A表示技术状态,α表示资本的产出弹性,β为劳动的产出弹性,在规模报酬不变时,该总量生产函数是一次齐性函数,即α+β=1。

二、数据的收集与整理

(一)产出指标

反应产出的指标很多,然而数据最容易获得而又最能反应经济增长的指标是 GDP[4]。因此,本研究采用我国1994～2008年的国内生产总值作为产出的度量。

(二)资本投入指标

由于该指标为存量指标,本研究以我国 1994～2008年固定资本投资总额为基础,各年的资本投入量为 1994年到该年的固定资本投资总额之和。

(三)劳动力投入指标

劳动力投入的度量,本研究采用 1994～2008年我国从业人员数量表示,因为从业人员数量很大程度上反映劳动力的投入。

表1 我国经济发展的相关数据

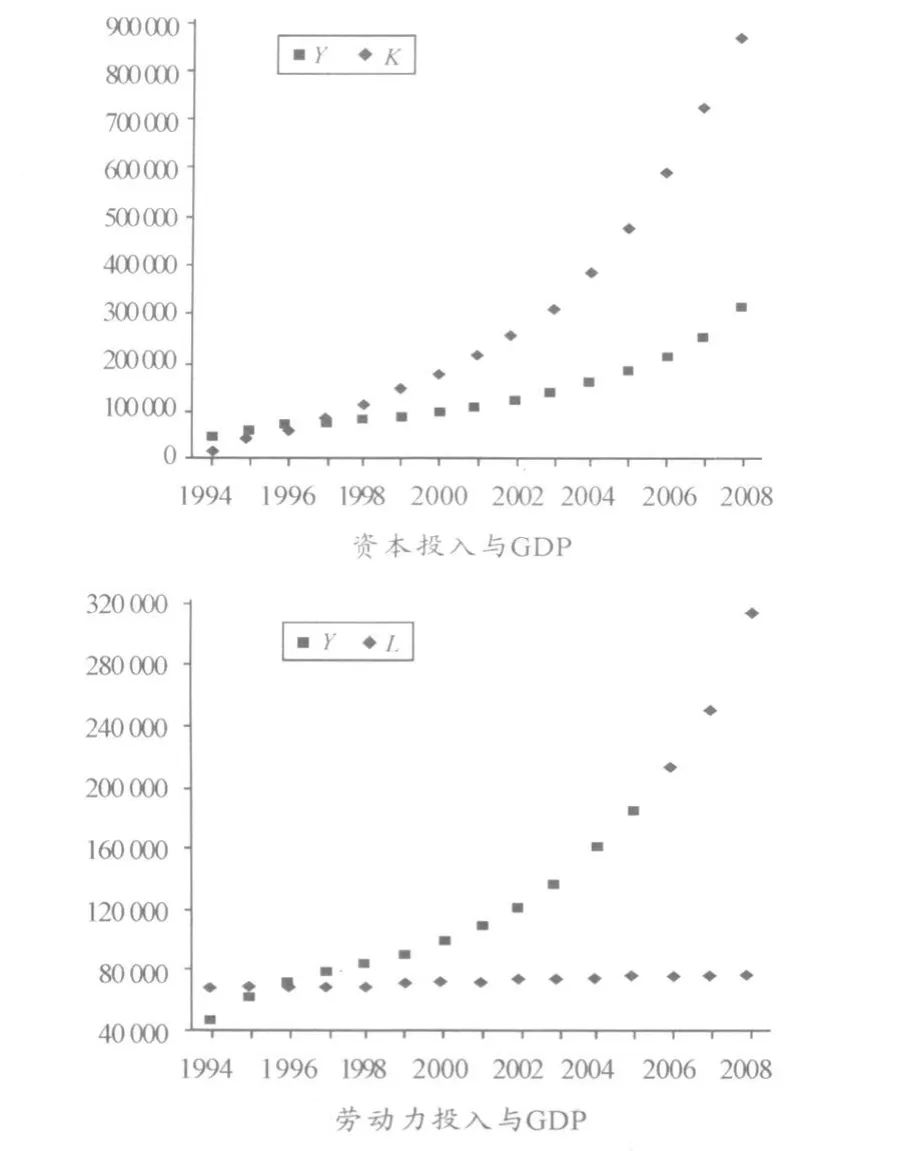
图1 各解释变量与被解释变量相关图

根据图 1可以判断,资本投入与 GDP呈正相关,劳动力投入与GDP呈正相关。

三、模型的建立

(一)模型初步拟合

由于柯布道格拉斯函数是幂函数形式的,属于非线性方程,因此,在正式进行回归之前要先将其转化为线性方程。对公式(1)两边同时取对数得:

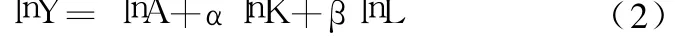
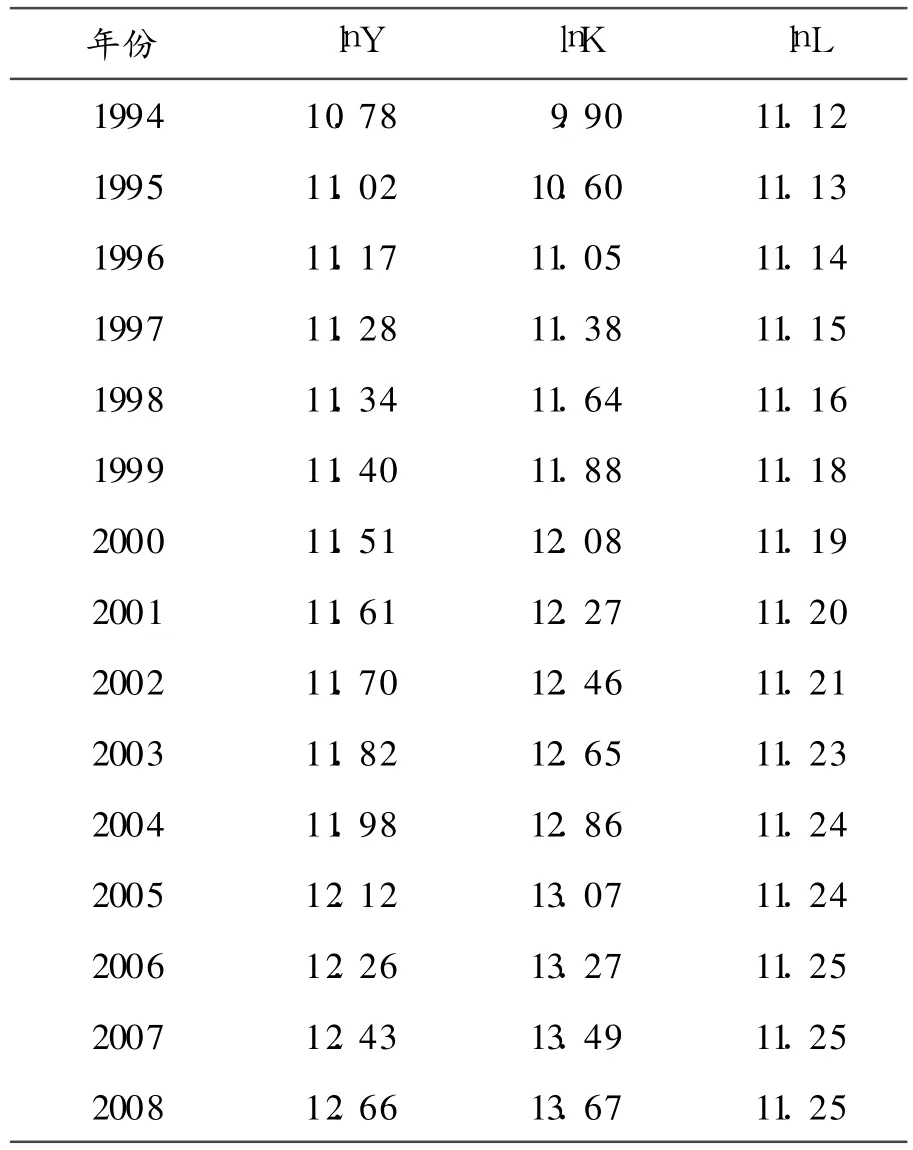
表2 根据公式(2)对初始数据进行调整

因为是时间序列,首先要进行平稳性检验,检验结果如表 3。

表3 时间序列平稳性检验结果

根据公式(2)利用Eviews对表2数据进行拟合如表4。

1)拟合优度检验:由于的值 R2=0.9489非常接近 1,因此可以判断回归线对样本数据的拟合度较高,总体回归效果显著。

2)各变量通过t检验,表明各解释变量对解释变量影响显著。

(二)模型检验

1)异方差检验:

本研究使用Eviews对该模型进行White检验如表5。

通过White检验,该模型不存在异方差。

2)自相关检验

本研究使用Eviews对该模型进行偏相关系数检验如图2。

根据偏相关系数可以判断该模型存在自相关。利用广义差分法对模型进行调整如表 6。响显著,而且从结果可以看出资本K的 t检验值大于劳动力投入L的 t检验值,说明资本对我国经济增长的影响更为显著。

3)多重共线性检验

由图3可见,lnY与lnK,lnL呈正相关。并且可算出lnK与lnL的相关系数为0.986 2,可见相关性较高,因此变量间存在共线性问题。为解决此问题,可利用α+β=1将模型由二元变为一元模型。

四、经济增长综合因素分析

根据索洛的经济增长模型,以柯布道格拉斯生产函数为基础,可建立分析模型:

式(3)中,y表示经济增长率,即GDP增长率,l表示劳动投入增长率,a表示技术进步增长率。劳动力投入、资本投入和技术进步对经济增长的贡献率分别可由αl/y、βK/y和1-αl/y-βK/y求得如表7。

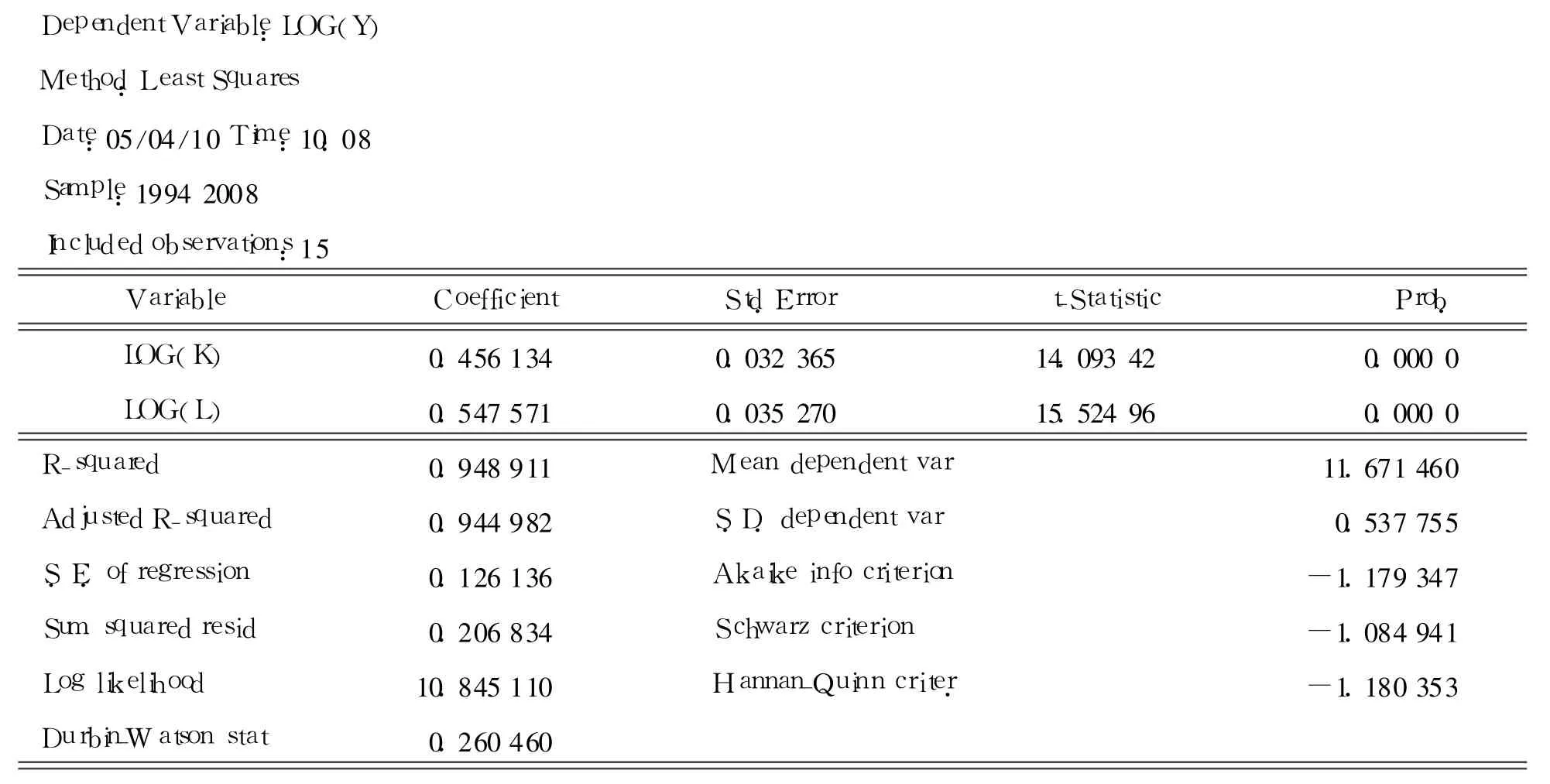
表4 利用表2数据进行拟合

表5 异方差检验Heteroskedasticity Test:White

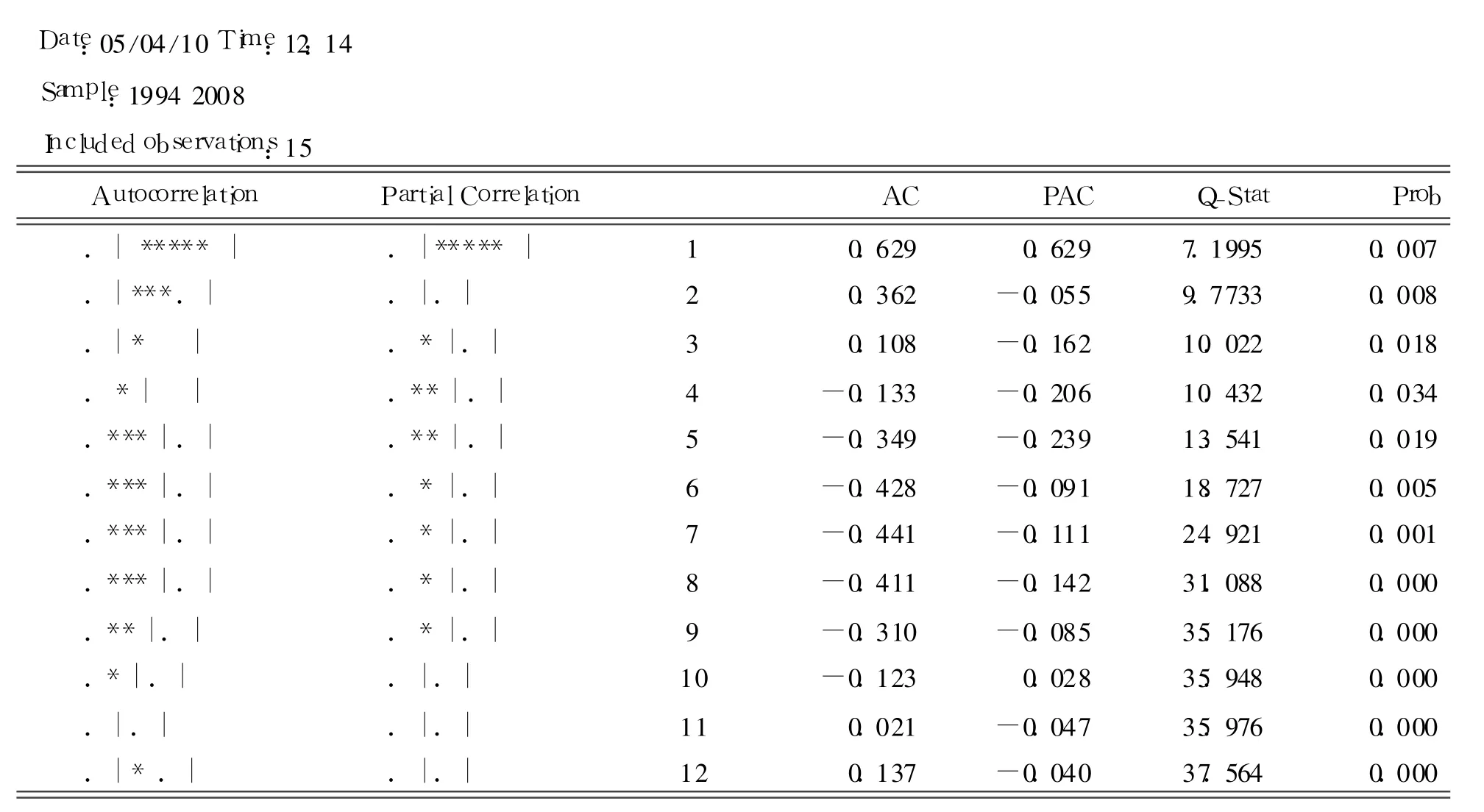
图2 偏相关系数检验

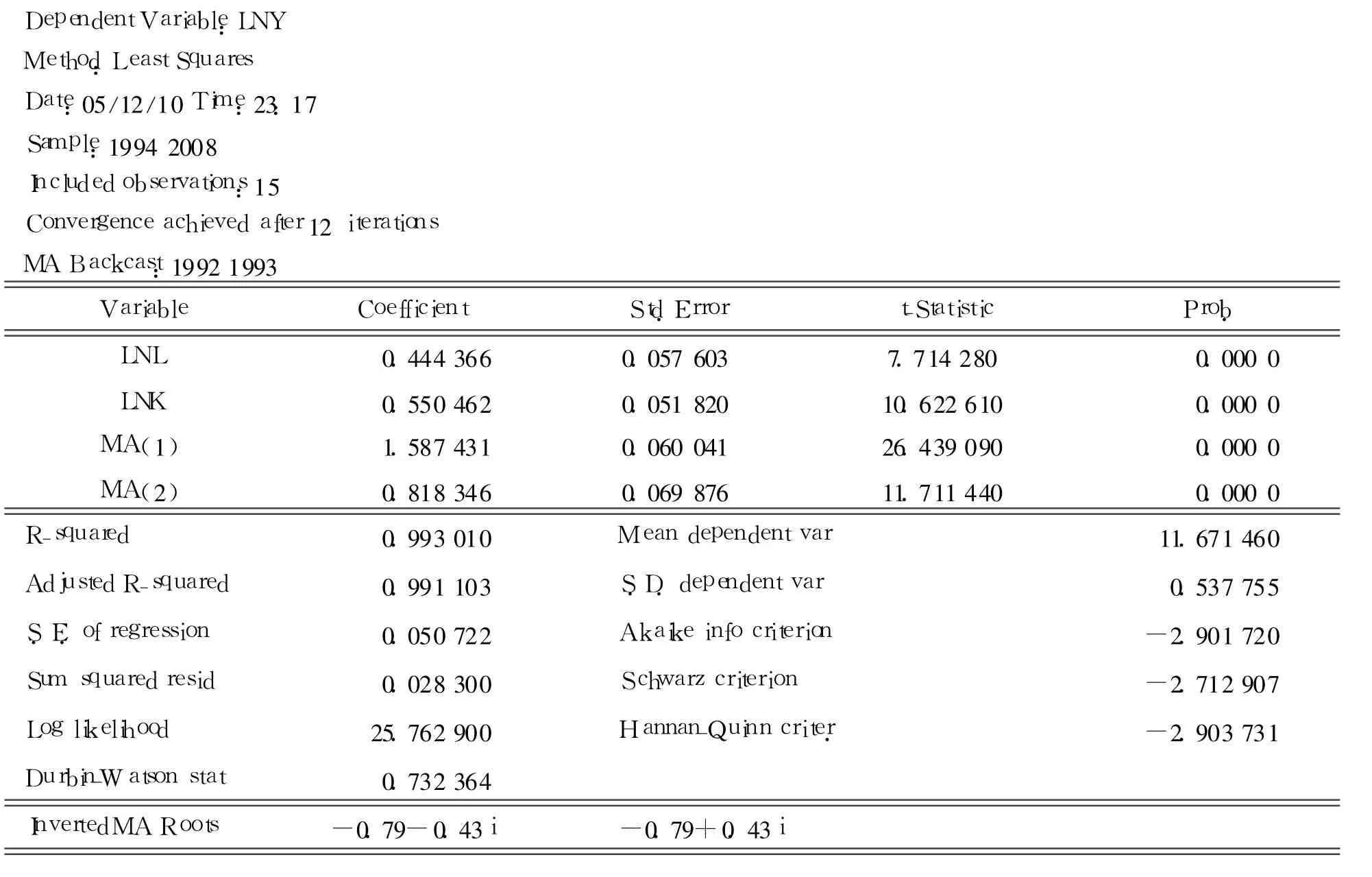
表6 利用广义差分法对模型进行调整

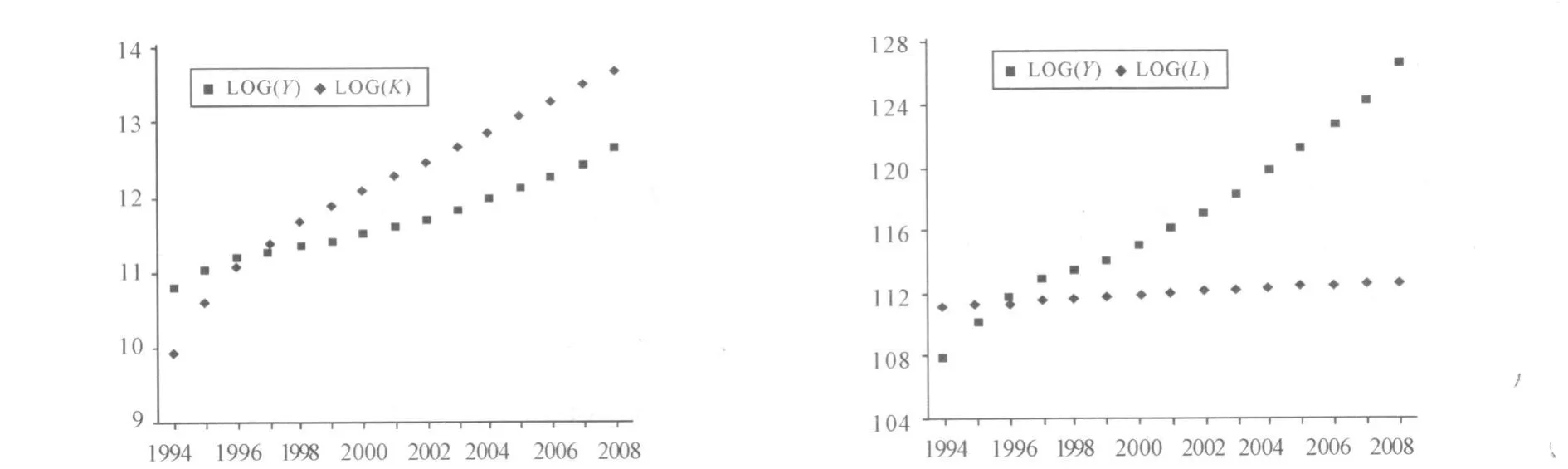
图3 lnK,lnL与lnY的相关图

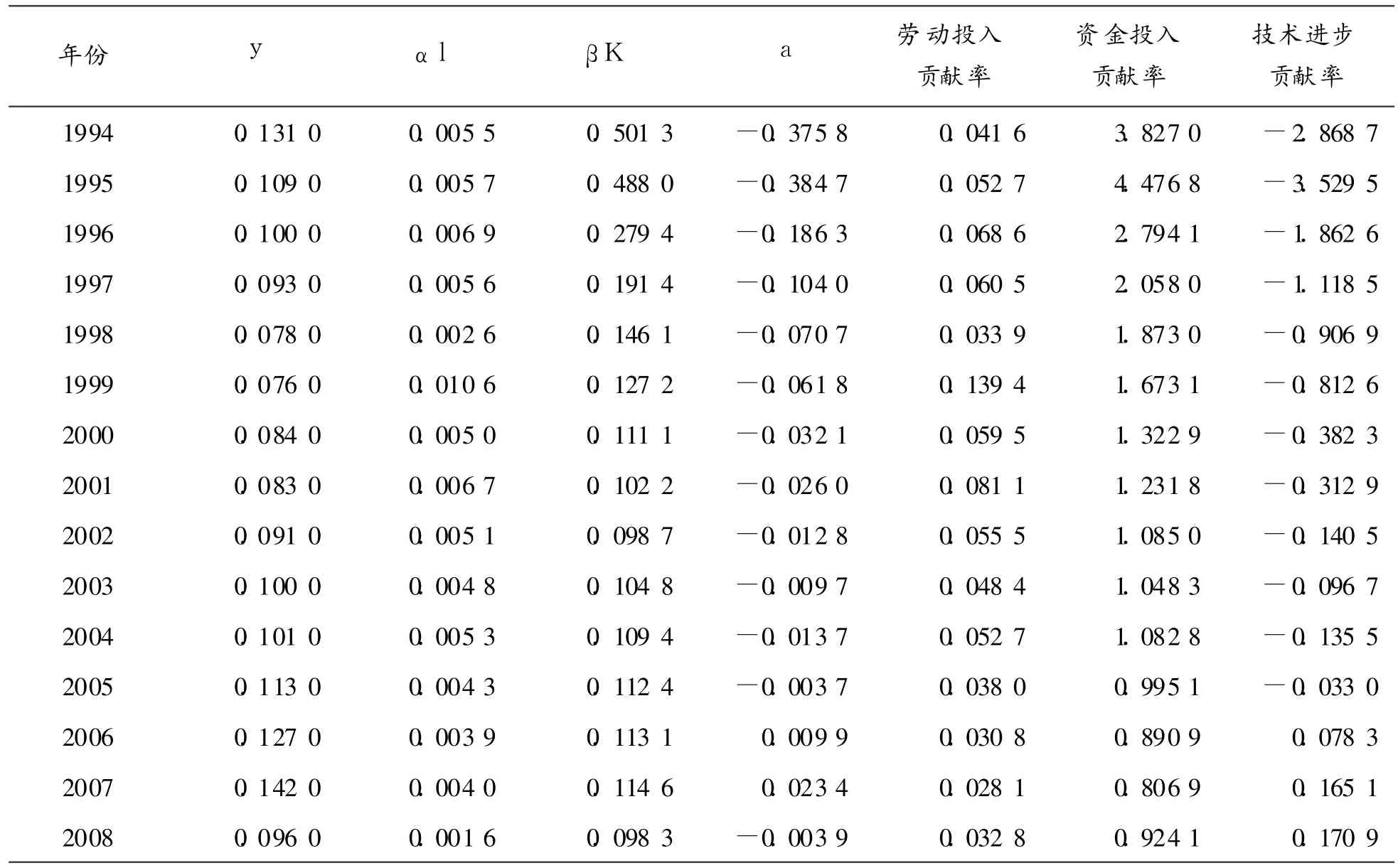
表7 经济增长综合分析

从表 6、图 4可以看到,中国经济增长中劳动投入的贡献率相对平稳,除 1999年以外,均低于 10%,从 2000年起均低于 5%。资本投入贡献率是三者中最高的,并有下降的趋势。可分为 3个阶段,1994—1997年期间,连续高于250%,随后有所下降但始终大于 200%,1998—2004年,呈下降趋势,但始终大于 100%,从 2005年以后降至 100%之内。与资本投入贡献相反,技术进步投入贡献率有逐步上升的趋势,从 2006年起,技术进步贡献率有明显的提高,开始为正,并逐渐增大,并在 2007年时超过劳动力投入贡献率,之前始终为负值。总的来看,从 1994—2008年间,我国经济增长以资本推动为主,其平均贡献率为 173.93%,其次是劳动力贡献率,其平均贡献率为 54%[5]。

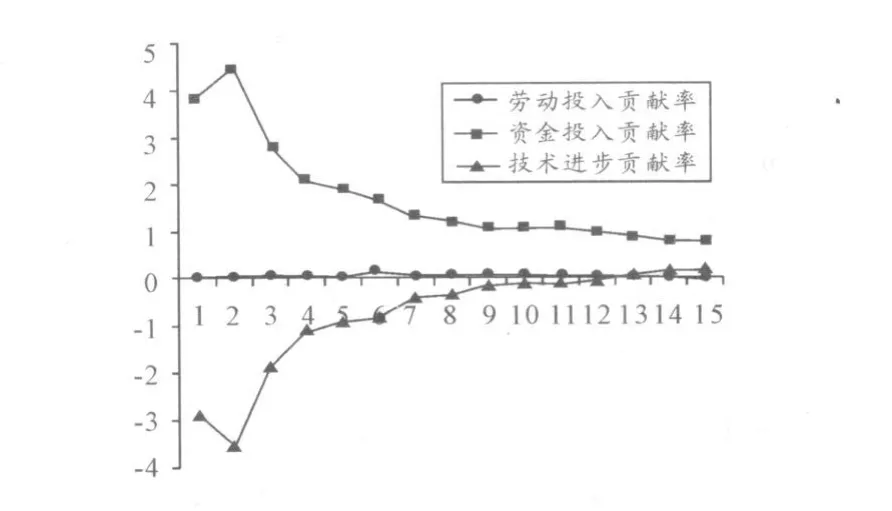
图4 综合因素贡献率

[1] 赵卫亚.计量经济学教程[M].上海:上海财经大学出版社,2003.

[2] 戴维◦N◦韦尔.经济增长[M].北京:中国人民大学出版社,2007.

[3] 罗伯特.M.索洛.经济增长因素分析[M].北京:商务印书馆,1991.

[4] 赵彦云.宏观经济统计分析[M].北京:中国统计出版社,2000.

[5] 任莎娜,楼凯旻.改革开放 30年我国经济增长因素的实证分析[J].中国商界,2009(8).

(责任编辑 张佑法)