带有弹性边界支撑梁的多宗量反问题数值求解

杨海天， 杨 博， 李哈汀

（大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116024）

0 引 言

如何根据实际情况，合理考虑力学建模中边界条件的影响，是一个值得探讨的问题［1］.建模过程中边界条件的不准确，将会导致结果的偏差.以悬臂梁为例，实际情况往往可能是在约束端允许有小量位移与转角（可被当成一种弹性支撑）.如单纯将约束假设为固支，则计算结果会出现较大偏差.这时将弹性支撑而不是固支作为边界条件可能更为合理.问题是如何确定这些等价弹性支撑的弹性参数.

求解带有弹性元件边界条件的反问题，是确定这些弹性参数的方法之一.对此国内外已有一些相关的文献报道，如文献［2］以梁在静力作用下的挠度为已知信息，利用神经网络对支撑弹簧刚度进行了识别，但需要大量的网络训练以提高精度，且没有考虑噪声影响；文献［3］提出以模态参数作为目标函数用牛顿法识别边界支撑刚度和边界质量，但没有考虑弯曲相关的弹性支撑；文献［4］在支撑刚度的识别中，对牛顿法和遗传算法进行了比较，发现牛顿法对初始解的选取较敏感；也有不少学者用频率响应函数法识别连接参数［1］，早期的频率响应函数（FRF）法对连接处的噪声较敏感，文献［5］由此进行了改进；文献［6］探讨了坐标缩减对频率响应函数法识别结果的影响；文献［7］对动力弹性边界优化设计的有关问题进行了综述.

以上工作主要围绕梁弹性边界上相关参数的反演展开，似未见到弹性边界相关参数与梁本构参数组合识别的文献报道，而实际问题中，梁的本构参数可能是未知的或在使用过程中发生变化.本文通过带有弹性边界梁的静力有限元方程，推导出梁的弹性边界／本构参数多宗量静力反演数值模型，采用L－M（Levenberg－Marquardt）算法［8～12］进行求解，可同时对弹性边界条件及梁的本构参数进行识别.

1 控制方程及其有限元离散

图1所示为Bernoulli－Euler梁，梁长为L，集中力f作用于x＝L0处.

图1 带有弹性支撑的梁Fig.1 A beam with elastic supports

其控制方程和边界条件为［13］

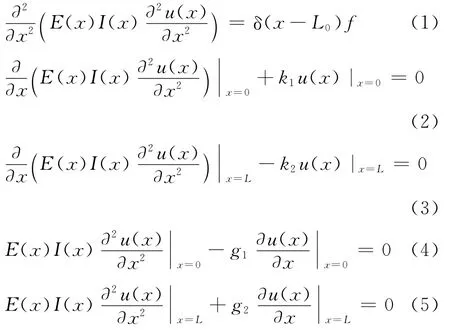
其中E为弹性模量，I为惯性矩，u为梁的横向位移，k1和k2为横向弹性支撑刚度，g1和g2为弯曲弹性支撑刚度.

系统的有限元方程可写为［14］

其中K、Y和F分别代表总刚度阵、总节点位移向量和总节点荷载向量.

其中G为单元节点自由度转换矩阵［13］，l为单元长度，N为二节点Hermite单元的形函数矩阵.

2 模型求解

未知参量ki、gj、Ek的识别可通过以下泛函的极小化实现.

式中：R（X）＝yp（X）－ym；yp（X）、ym分别为节点位移向量的预测值和测量值；ki和g j为未知弹性支撑参数；Ek为任意未知单元的弹性模量.

计算流程为［8］

Step 1 选取变量初值X0，设置迭代步n＝0及ε（误差容限）；

Step 2 计算R（X n）及R（X n），通过式（12）求解D n；

Step 3X n＋1＝X n＋D n，并令n＝n＋1.

Step 4 如果‖D n‖≤ε，则停止迭代；否则执行Step 2.

3 噪声处理

按照文献［15］的方法注入噪声：

其中为不含噪声的已知信息，ξ是一个服从标准正态分布的随机变量，Ns表示噪声水平.对于每一个给定的Ns都由ξ生成40组y＊.

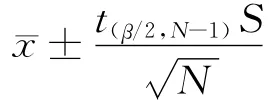
置信区间为其中表示反演结果的平均值，S表示标准差，t表示N－1个自由度的t－分布，N表示样本容量，置信度为1－β.

4 数值算例

算例1 边界条件的影响

图2 弹性支撑悬臂梁Fig.2 A cantilever beam with elastic supports

考虑图2所示带有弹性支撑的悬臂梁，梁长L＝0.5 m，单元长度l＝0.01 m，弹性模量E＝210 GPa，惯性矩I＝10－6m4，密度ρ＝7 860 kg／m3，荷载大小f＝5 000 N.u和θ为带有弹性边界条件梁的位移和转角，u0和θ0为相同荷载条件下固支边界梁的位移和转角.k为106～1010N／m，g为104～109N·m／rad［16］.表1给出了考虑不同边界条件下的解.不难看出，随梁端刚度的减小，边界条件为弹性支撑的解与固支条件的解相比发生了明显变化.

表1 位移转角比较Tab.1 The contrast of displacement and angular displacement

算例2 弹性支撑与弹性模量的组合识别

考虑图1所示两端带有弹性支撑的梁，将梁均匀划分为50个单元，对弹性支撑的刚度k1、g1和梁的弹性模量E20进行组合反演.Ei＝210 GPa（i＝1，2，…，19，21，…，50），k2＝1×105N／m，g2＝3×103N·m／rad，L0＝0.3 m，其他参数与算例1中相同.

采用3个点的转角作为已知信息，测点位置和ξ的最大值见表2，计算结果如表3、4所示.

表2 测点位置和ξ的最大值Tab.2 The location of measuring points and the maximums ofξ

表3 10%噪声下弹性支撑和弹性模量的组合识别Tab.3 Combined identification of elastic supports and modulus of elasticity at 10%of noise

表4 5%噪声下弹性支撑和弹性模量的组合识别Tab.4 Combined identification of elastic supports and modulus of elasticity at 5%of noise

计算结果表明：当按式（17）考虑噪声的影响时，本文所提算法可有效地对弹性支撑的刚度和梁的本构参数进行识别，测点越接近待识别参数所在单元的位置识别效果越好.

5 结 语

本文的主要贡献是建立了一个梁的弹性边界／本构参数的静力组合反演数值模型，可同时对弹性边界条件及梁的本构参数进行识别.数值验证表明，本文所提出的模型与方法是正确可行的.在本文工作的基础上，作者正结合有关实验，开展梁的弹性边界／本构参数的动力组合反演研究，以期为更合理地确定边界条件／本构参数提供有效的新方法.

［1］KIM T R，WU S M，EHMANN K F.Identification of joint parameters for a taper joint［J］.Journal of Engineering for Industry，1989，111（3）：282－287

［2］郭国会，易建伟.神经网络在梁的边界条件识别中的应用［J］.湖南大学学报（自然科学版），1998，25（4）：87－112

［3］刘玉明，易建伟.一种识别结构系统边界条件的新方法［J］.湖南大学学报（自然科学版），1999，26（2）：99－103

［4］易建伟，刘 霞.混凝土梁板类构件边界条件识别与研究［J］.湖南大学学报（自然科学版），2000，27（4）：81－87

［5］REN Y，BEARDS C F.Identification of joint properties of a structure using FRF data［J］.Journal of Sound and Vibration，1995，186（4）：567－587

［6］DAMJAN C，MIHA B.The influence of the coordinate reduction on the identification of the joint dynamic properties［J］.Mechanical Systems and Signal Processing，2009，23（4）：1260－1271

［7］高跃飞.结构动力学边界条件优化设计与工程实现方法研究［D］.西安：西北工业大学，2005

［8］王彦飞.反演问题的计算方法及其应用［M］.北京：高等教育出版社，2007

［9］LEVENBERG K.A method for the solution of certain non－linear problems in least squares［J］.Quarterly Journal of Applied Mathematics，1944，11（2）：164－166

［10］MARQUARDT D W.An algorithm for leastsquares estimation of nonlinear inequalities［J］.SIAM Journal on Applied Mathematics，1963，11（2）：431－441

［11］MORE J J.The Levenberg－Marquardt algorithm：implementation and theory［C］／／WATSON G A，ed.Numerical Analysis Proceedings of the Biennial Conference Held at Dundee.Berlin：Springer－Verlag，1978：105－116

［12］LIU G R，HAN X.Computational Inverse Techniques in Nondestructive Evaluation［M］.London：CRC Press Inc.，2003

［13］张 雄，王天舒.计算动力学［M］.北京：清华大学出版社，2007

［14］TABARROK B，CLEGHORN W L.Application of principle of least action to beam problems［J］.Acta Mechanica，2000，142（1）：235－243

［15］王登刚，刘迎曦，李守巨.二维稳态导热反问题的正则化解法［J］.吉林大学自然科学学报，2000（2）：55－60

［16］AGAPIOU J S.A methodology to measure joint stiffness parameters for toolholder－spindle interfaces［J］.Journal of Manufacturing Systems，2005，24（1）：13－20