强结构扰动理论在唯一稳态消谐法中的应用∶以零序电阻消除铁磁谐振分析为例
冯平,王尔智,王维俊
(1.解放军后勤工程学院机械电气工程系,重庆401311;2.沈阳工业大学电气工程学院,辽宁沈阳110178)
在中性点直接接地电力系统,如110~220 kV等中性点接地的电力系统,经常发生断口电容与电压互感器形成的铁磁谐振,给电力系统造成很大的危害.围绕这种谐振的机理及消除方法,国内外进行了广泛的研究[1-2].
从方法上看,目前对这种铁磁谐振问题所主要采用的方法有如下几种.第一是实验研究[3-4],即通过大量的实验数据得到各种经验结论.第二是进行数值模拟和仿真[5-6],通过建立模型,在大范围内改变参数,通过计算机计算得到或验证参数的范围.第三是理论研究[7-8],即对这种谐振建立相应的数学模型,通过对模型的理论分析,了解这种谐振的机理,并且寻找消除谐振的方法.这三种方法中,理论分析具有决定性的意义,主要有作图法[1,8]、谐波平衡法[5-6]、平面相图法[4],幅频法、描述函数法[1-3]、非线性动态系统理论[4,7]等.但由于该问题数学上的复杂性,目前采用的都是各种近似的方法,得到的结论和试验数据往往有一定的差距.因此,提出和发展新的分析铁磁谐振的方法,并对该问题进行更深入的分析是很有意义的.
对中性点直接接地系统铁磁谐振,利用零序电阻来消除是最理想的,因此人们一直在进行探索.大量实验表明[7-8],在某些情况下,零序电阻可以消除这种谐振,但在某些情况下又不能消除谐振.究竟在哪些情况下可以消除谐振,满足的参数关系是什么;而哪些情况下不能消除谐振,其原因又是什么,由于缺乏深入的理论分析作指导,这一工程上迫切需要解决的主要问题至今一直没有确切的答案.
唯一稳态消谐法是近年出现的消除非线性系统谐振新的分析方法[6].该方法的基本思想是如果非线性系统存在一个非谐振的正常解,并且该系统具有唯一的稳态,则此时对应的条件就是系统不发生谐振的条件.本文将这一方法应用在零序电阻消除中性点接地电力系统铁磁谐振的分析中,以强结构扰动理论为工具,得到了相应的消谐条件.本文的结果表明,消除谐振的条件可以用一个矩阵的稳定性条件来决定,并用数值模拟进行验证,表明结果正确,同时也说明唯一稳态消谐法有效性.
1 等效电路及其数学模型
以图1的电路作为中性点接地电力系统铁磁谐振的模型[1].

图1 中性点接地电力系统中的三相铁磁谐振的等效电路Fig1.Equivalent circuit for neutral groundingsystemin ferroresonance
图1中三相电源电势为∶

C>0,为断口电容与对地电容的等效电容,RN>0为零序消谐电阻.La>0,Lb>0,Lc>0为铁磁式电压互感器的非线性电感,La,Lb,Lc具有相同i-ψ曲线,并可表示为分段线性形式如图2所示.

Fig 2.Flux-current curve
设,;,为系统a相的两个不同的稳态解.并且记

同样对b相

对c相
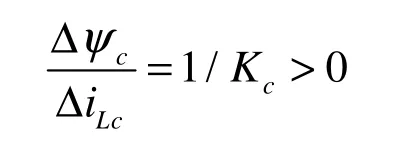
并设:

对图1,不难得到其状态方程为:

式(1)中,各量参考方向如图1,iLa~ψa,iLb~ψb,iLc~ψc的关系由图2确定.
对电路周期解存在性,可以证明,系统至少存在一个以T为周期的解[11],假设对于状态方程组式(1)的任意两个有界的稳态解为:
当系统受到扰动时,磁链及系统电压都要发生改变,令:

于是得到对应于状态方程组式(1)的增量微分方程为:

注意到:

式(2)又可以写为

于是,式(3)改写为

考虑式(4)的一般形式:

显然,如果式(5)的零解X=0是全局渐进稳定的,即:

则式(1)、即图1所示电路的稳态唯一,即系统的不谐振条件.下面推导消除系统谐振条件.
2 电路唯一稳态的条件(消除谐振条件)的求取
唯一稳态消谐法是近年出现的消除非线性系统谐振新的分析方法[6].该方法的基本思想是如果非线性系统存在一个非谐振的正常解,并且该系统具有唯一的稳态,则此时对应的条件就是系统不发生谐振的条件.按照这一方法,对于图1和状态方程(1),大量实验和运行经验表明其有多个稳态解,其中最常见的稳态解,就是没有发生谐振时,对应于系统正常工作状态的稳态解.系统的其他非正常的稳态解,则是由于扰动,引起C与L之间的铁磁谐振造成的稳态解.显然这些非正常的稳态解对于系统是有害的,如果我们能够使经扰动后的非正常稳态解趋于正常的稳态解,即使系统的稳态解唯一,那就可以达到消除系统铁磁谐振的目的.这样,消除铁磁谐振的问题此时就转化为求系统的唯一稳态的问题.
为了求得系统的唯一稳态,我们将式(5)改写为:

首先,我们介绍如下的引理:
引理1任何在复平面上的对称于实轴X的平面区域均可用代数方程[12]:

引理2[12]对于实数矩阵:

其特征根在区域Ω2内的条件是:
对任意对称正定的实矩阵Q,存在唯一正定的实矩阵P满足如下的Lyapunov方程:

其中

于是有如下定理:
定理1对于式(5),如果A是Hurwitz阵,并且

这里P是Lyapunov方程的对称正定解,则式(1)有唯一稳态.
证明:首先,对于任何n阶实数矩阵W,W1,W2,记:

即式(5)的零解是全局渐近稳定的,式(1)有唯一稳态.
证毕.
下面根据定理1,推导消除谐振的条件.
比较式(3),式(5),有:

根据定理1,可以得到其对应的消除谐振的条件为定理2.
定理2对于图1所示电路,其不发生谐振的条件为:

因此,根据定理2,对于不同的实际参数,选择不同的RN使系统不发生谐振.根据文献[5]取参数(均为标幺值):
E=1电流-磁链曲线,有:

按照KL的定义,有
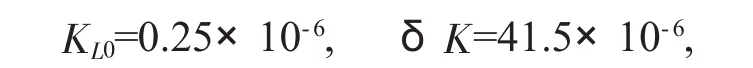
假设各相电流磁链曲线特性相差10%.当C=0.33334时,将数据代入得到定理2,则RN变化范围为:

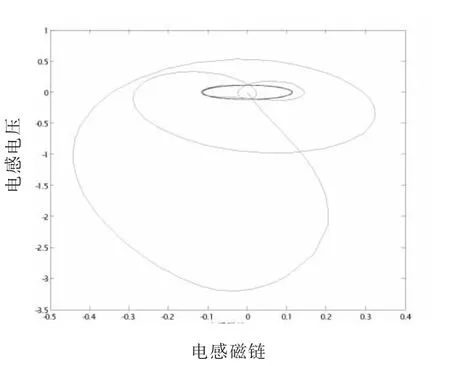
图3 电路稳态相Fig3.Circuit’s steadystate diagram
系统无谐振出现.
3 数值模拟与讨论
取不同的参数,在不同的初始条件下,对电路进行模拟仿真,以检验电路是否发生谐振.初始条件顺序为:磁链,电容电荷,时间,初始条件按文献[5]选定.
模拟结果表明,如果电路参数满足定理2的条件,则
电路无论在何种初始条件下,虽然经过非常复杂的振荡过程,其稳态都是唯一的,最终所有解都将趋近正常解,不会出现铁磁谐振,验证了本文给出的条件的正确性.

4 结论
本文根据唯一稳态消谐法的基本思想,利用强结构扰动理论,分析了零序电阻消除中性点接地电力系统铁磁谐振的参数条件,得到了相应的消谐条件,数值模拟验证表明结果正确,同时也说明唯一稳态消谐法的有效性.
∶
[1] 解广润.电力系统过电压[M].北京:水利电力出版社,1985.
[2] 张纬钹,高玉明.电力系统过电压与绝缘配合[M].北京:清华大学出版社,1988.
[3] Jacobson D,Menzies PW.Stbailiy domain calculations of period-l ferroresonnace in a nonlinear resonant circuit[J].Power Delive,IEEE Transactions on,2002,17(3):865-871.
[4] 郑盛琼,陈维贤,鲁铁成.110~220 kV变电所中互感器引起的铁磁谐振及吸能消谐[J].高压电器,1996,18(6):26-30.
[5] Thor Henrik sen.How to avoid unstable time domain responses caused by transformer mod els[J].IEEE Trans.on Power Delivery,2002,17(2):516-522.
[6] 冯平,王尔智.中性点接地电力系统三相铁磁谐振理论分析[J].电工技术学报,2004,23(4):35-39.
[7] Li Y G,Shi W.A Systematical method for suppressing ferroresonance at Neutral-Grounded substations[J].IEEE Transactions on Power Delivery,2003,18(3):1009-1014.
[8] 李兴斌,王晨新.断路器均压电容引起的铁磁谐振分析[J].东北电力技术,1994,24(9):39-43.
[9] 贾红琴.电磁式PT所致铁磁谐振过电压分析及抑制[J].高电压术,2000,43(1):69-70.
[10] 冯平.一种混沌分析与抑制方法及其在电力系统铁磁谐振中的应用[D].沈阳:沈阳工业大学,2010,7.
[11] 尤秉礼.常微分方程补充教程[M].北京:人民教育出版社,1981.
[12] 杨开字.矩阵分析[M].哈尔滨:哈尔滨工业大学出版社,1988.

