大惯性对象控制器参数寻优的目标函数研究

马 平 潘洪洲 周宇华

(华北电力大学控制与计算机工程学院，河北 保定 071003)

大惯性对象控制器参数寻优的目标函数研究

马 平 潘洪洲 周宇华

(华北电力大学控制与计算机工程学院，河北 保定 071003)

传统目标函数在大惯性被控对象PID控制器参数寻优过程中存在超调量过大、调节时间过长且对不同对象缺乏灵活性等问题。基于最优控制理论，并结合Matlab环境中对其参数进行不同目标函数的遗传算法寻优的大量仿真试验，提出了一种适用于大惯性对象控制器参数寻优的变权综合型的目标函数。通过仿真试验，证明了变权综合型的目标函数具有比较好的灵活性，且其寻得的参数明显优于传统目标函数。

大惯性对象 参数寻优 遗传算法 目标函数 仿真

0 引言

随着科学技术的发展、自动化程度的提升和生产规模的扩大，被控对象通常呈现出大延迟、大惯性和多扰动的特性。这种被控对象对当前施加的控制量需要经过一段时间后才会在对象输出中反映出来。因此，在调节过程中时常有动态偏差大、调节时间长等问题出现，这些问题往往导致生产过程动态品质的下降［1-2］。

面对复杂的被控对象和高要求的产品质量［3］，仅凭人工经验或传统的目标函数将无法使控制系统达到最佳的控制效果。本文在传统目标函数的基础上，提出一种适用于大惯性难控对象的变权综合型目标函数。仿真结果证明，改进型目标函数所寻的PID控制器参数的控制效果明显优于传统目标函数。

1 传统目标函数

1.1 单项性能指标型

单项性能指标型目标函数是以系统的输出响应特性为指标的［4-5］，主要有衰减率、超调量、残余偏差和调节时间等。一般工业控制系统往往有多项性能指标的要求，因此，可以根据不同的需求来选取这些指标。但单一的性能指标不能保证控制效果达到最优，所以需要通过采用多个单项性能指标进行变权综合的方法来解决。

变权综合是对常权综合的一种改进［6］，其基本思想是在一个组评价参数的综合评价中，不采用常权加权平均的方法求综合评价结果，而是对一组评价参数的某些部分进行“惩罚”或“激励”，即减小权重或加大权重，并在此基础上进行综合评价，从而使评价结果更趋合理。

1.2 误差积分指标型

误差积分指标型目标函数是系统在过渡过程中被调量偏离其新稳态值的误差沿时间轴的积分。无论是误差幅度大或是时间拖长都会使误差增大，因此，它是一类综合指标，其值越小越好。

误差积分有多种形式［7］，常用的有误差积分(IE)、绝对误差积分(IAE)、平方误差积分(ISE)以及时间与绝对误差乘积积分(ITAE)4种。它们的积分公式如下:

误差积分:

绝对误差积分:

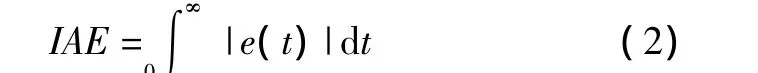
平方误差积分:

时间与绝对误差乘积积分:

采用不同的积分公式，表示估计整个过渡过程优良程度时的侧重点不同。

典型大惯性对象电厂锅炉的串级系统PID控制器参数寻优的示意图如图1所示［8］。

图1 PID控制器参数寻优Fig.1 Optimization of the parameters of PID controller

将上述4种误差积分型目标函数分别作为遗传算法的适应度函数，对PID控制器参数进行遗传算法寻优，通过被控系统输出响应曲线来分析这4种目标函数优缺点。

图1中被控系统的模型传递函数G1、G2分别如下所示［9］:

按图1方案，对对象的PID控制器参数进行寻优，被控对象对阶跃给定值扰动的响应结果如图2所示。

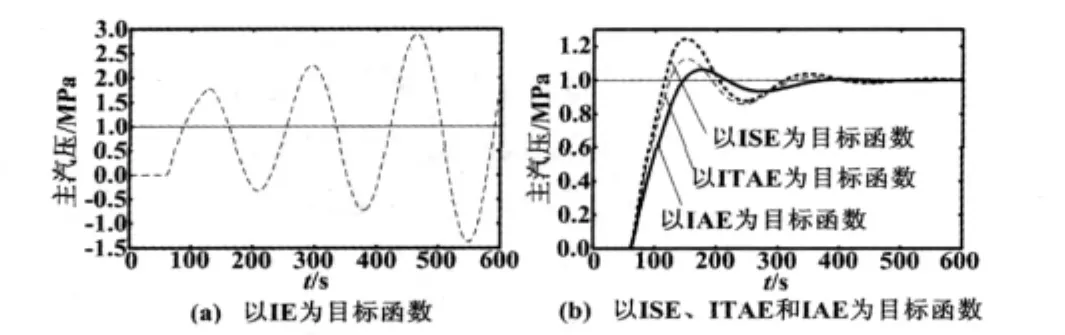
图2 响应结果Fig.2 Response results

从图2中可以清楚地看到，以IE为目标函数寻优，由于系统处于振荡时，误差有正有负，积分使正负误差相消，所以当IE为极小时，系统接近于等幅振荡。以ISE为目标函数寻优对系统误差没有时间上的约束，且平方项对较大的系统误差有较强的抑制作用，对小误差考虑较少［10］。当ISE为极小时，系统通常有较快的响应速度，从而导致了系统较大的振荡，产生过大的超调，相对稳定性差。以IAE为目标函数寻优与ISE相似，没有时间的约束，但其对小误差的约束强于ISE，所以控制系统超调小于ISE，不过调节时间较长。以ITAE为目标函数寻优对系统误差具有时间上的惩罚作用，调整时间越靠后的误差，与之相乘的时间系数就越大。因此，当ITSE为极小时，系统瞬态响应的振荡性比ISE指标小。

2 改进的目标函数

误差积分指标有一个共同的缺点，就是它们的指标过于单一，并不能都保证控制系统具有最合理的超调量、调节时间和稳定性等。特别是IE指标寻优得到的等幅振荡是必须避免的，而对于大惯性对象的控制难点正在于动态偏差大、调节时间长。针对上述特性，引入了着重惩罚过渡时间长的误差积分指标ITAE、超调量指标和调节时间指标，再将三者进行变权综合来权衡控制系统的最大动态偏差和调节时间，设计了一个适于大惯性对象的变权综合型目标函数。

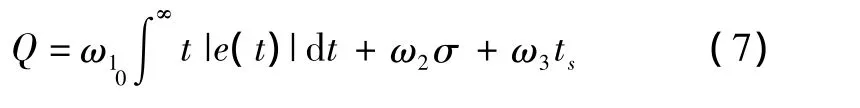
式中:ω1、ω2、ω3为权值;σ 为超调量;ts为调节时间。

3 仿真研究

3.1 改进效果验证

基于Matlab的仿真平台与遗传算法寻优程序，将4种传统的误差积分目标函数与改进的目标函数应用于如图1所示的电站锅炉仿真实例中进行比较，所得结果如图3所示。

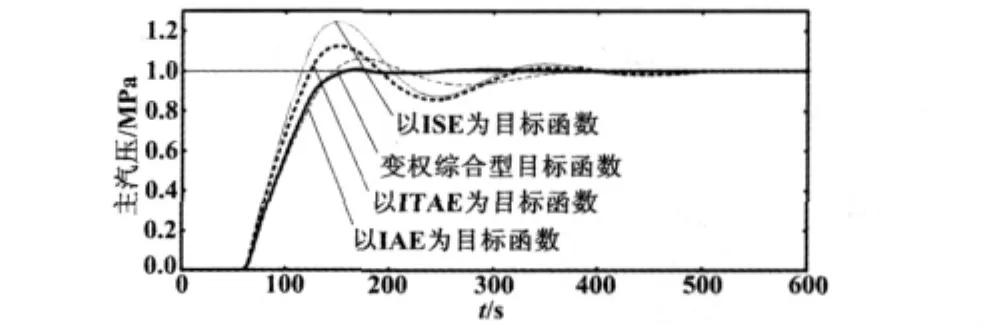
图3 仿真实例比较结果Fig.3 Comparison of the simulation examples

统计图3中4条响应曲线数据所得的寻优结果如表1所示。

表1 目标函数寻优结果Tab.1 Optimization results of objective functions

结合图3和表1可以看出，以变权综合型为控制器参数寻优目标函数所得的控制曲线，无论是在超调量指标还是在调节时间指标方面都要小于其他3种传统型目标函数。由此说明了通过改进型目标函数所寻得的控制器参数明显优于其他3个目标函数。

3.2 灵活性验证

保持改进的目标函数的ω1和ω3不变，通过对ω2进行参数改变，即对目标函数的超调量权值赋值为50、200、500，得到的仿真结果如图4所示，其权值设置值与曲线统计数据如表2所示。

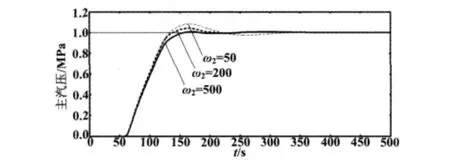
图4 仿真曲线Fig.4 Simulation curves

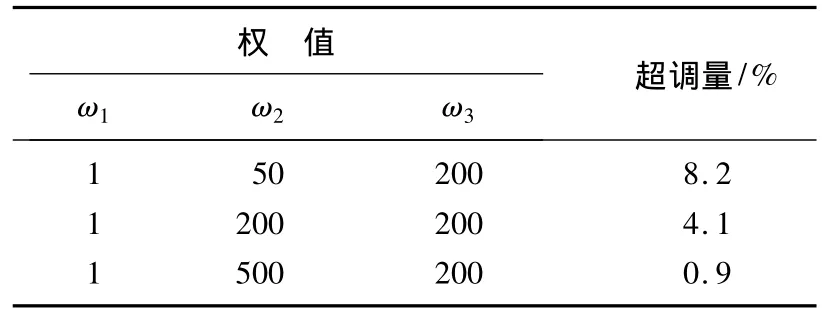
表2 曲线的目标函数权值Tab.2 The objective function weights of the curves

结合图4和表2可以清楚地看到，随着超调量权值的增大，控制曲线的超调量越来越小。同样地，通过保持ω1和ω2不变，对ω3进行参数设置，可以得到调节时间随ω3的增大而减小的结论。所以，通过上述仿真试验可以说明，变权综合型目标函数可以根据不同的系统需要进行权值设置并寻找系统控制器的最佳参数，从而达到最佳的控制效果，具有一定的灵活性。

4 结束语

由于被控对象越来越复杂，控制精度的要求和智能化程度的不断提高，使得衡量控制性能的目标函数发挥着越来越重要的作用，在智能化控制过程中它将决定着控制品质的好坏。本文设计了一种变权综合型的目标函数，仿真试验结果表明，其对大惯性控制系统的控制器参数进行寻优所得的结果明显优于传统型目标函数，且可以根据不同被控制对象需要，改变其权值来寻得控制系统的最佳控制器参数，具有一定的灵活性。

［1］黄宇，韩璞，李永玲.主汽温系统模糊自适应内模控制［J］.中国电机工程学报，2008，28(23):93-98.

［2］郭鹏.灰色预测自适应内模控制在电厂过热汽温控制中的应用［J］.动力工程，2007，27(4):560-563.

［3］翟丁，张庆灵，刘国义，等.一类时滞线性系统的鲁棒非脆弱控制器设计［J］.控制与决策，2006，21(5):559-562.

［4］何晋元，周国鹏.用于控制器参数寻优的目标函数研究［J］.微计算机信息，2006(3S):86-88.

［5］周国鹏，柳学坤，何晋元.基于控制系统优化的ITSE目标函数的研究［J］.微计算机信息，2006，22(8):46-47.

［6］刘永强.变权综合型目标函数及其在控制系统优化设计中的应用［J］.淮海工学院学报:自然科学版，2005，14(4):24-27.

［7］金以惠.过程控制［M］.北京:清华大学出版社，1993.

［8］唐义军，严建华，朱永超，等.面向对象的火电厂主汽温控制方法［J］.动力工程，2007，27(5):742-747.

［9］夏猛.基于辐射能信号的电站锅炉燃烧控制系统研究［D］.武汉:华中科技大学，2005.

［10］杜海峰，王孙安.目标函数对神经网络性能影响的研究［J］.西安交通大学学报:自然科学版，2002，36(1):54-57.

Research on the Objective Function of Optimal Parameters for Large Inertia Objects Controller

The optimisation of parameters for PID controller used for large inertia controller object by adopting traditional objective function features excessive overshoot，long settling time and lack of flexibility for different objects.To overcome these demerits，based on optimal control theories，and combines with many simulation experiments of optimising parameters by genetic algorithm with different objective functions under Matlab environment，the variable weight synthesizing objective function that is suitable for large inertia object to optimise parameters of controller is proposed.The simulation experiments verify that such objective function offers better flexibility，and the parameters it obtains are more superior to those from traditional objective functions.

Large inertia object Optimal parameters Genetic algorithm Objective function Simulation

TP273.1

A

修改稿收到日期:2010-08-24。

马平，女，1961年生，1990年毕业于华北电力大学热能工程专业，获硕士学位，教授;主要从事智能控制理论及其与应用方面的研究。