力的第四要素

张宪恩，陈朝军，宣志刚

(1.攀枝花攀钢集团设计研究院有限公司，四川攀枝花617023;2.新钢钒技改部，四川攀枝花617000)

力的三要素概念(大小、方向、作用点)已深入人心，解决了自然界中大部分力学问题。力的三要素作用的对象是一个单体、一个单质点。本文分析、论述力的第四要素。

1 研究对象

让我们假设，有a球、b球两个球用杆c连接(见图1)，a球、b球、杆c组成了一个系统(以下简称系统)。现在，让我们分析一下在a球受力后，b球的运动规律。记a球、b球的质量分别是ma、mb，杆c无质量，只有刚度。杆的刚度有两种，其一，杆的抗侧移刚度，抗侧移刚度记为kc1;其二，杆的纵向刚度，其纵向刚度记为kc2。

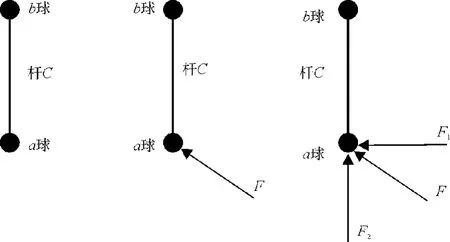
图1 球的受力

首先，a球受力多种多样。无论a球受怎样一个力，它都可以简化为两个力:一个力(记为F1)是作用于a球、垂直于杆的轴线;一个力(记为F2)是作用于a球，平行于杆的轴线(见图1(c))。F2作用时，系统只作平动。F1作用时，若无别的什么力，系统开始受力时作以b球为圆心、杆的长度为半径的圆周运动，随后，由于a球作圆周运动，就要产生离心力，那么系统作沿着离心力与F1合力的方向的运动。这个运动不是本文研究的对象。本文研究的对象是，在F1作用下，在a球上施加一个使系统沿F1方向运动的弯矩，使系统沿F1方向运动的规律。F2已使系统沿F2方向运动，其运动规律与F1之相同，所不同的是，杆的纵向刚度远大于杆的抗侧移刚度。下面仅论述F1作用下，系统沿F1方向的运动规律。

2 运动形态分析

现在让我们分析系统在F1作用下沿F1方向的运动。当a球作用F1时，a球就运动，那么b球将怎么样呢。这时，b球有三种状态:b球先于a球运动而运动;b球与a球同时运动;b球后滞于a球运动而运动。对第一种状态是绝对不会发生的，因b球未先于a球受力。对于第二状态，当F1缓慢由小向大增加时就发生了，a球、b球、杆c同时运动。这时，a球、b球、杆c组成了一个刚体，它们之间无运动差异。对第三种状态，当F1很快地由小向大增加时就发生了。让我们想象一下系统的运动，a球受力后很快位移，b球静止，杆c产生弯曲。b球后滞于a球运动。我们称力F1由小(大)向大(小)的增加(或减少)、或力的方向改变、或二者都有，为力F1的变化速度。

那么，力的变化速度多大时，系统组成的系统不是刚体。让我们分析a球在F1作用下运动、b球的运动原理。a球在F1作用下运动，由于杆的抗侧移刚度，使得a球在杆中产生剪力，杆又将这个剪力传至b球，使b球受力，b球受力后就运动。但是在F1作用下a球运动，由杆的抗侧移刚度、b球的质量，使得b球运动后滞于a球。

3 质点反应的概念

这里引入一个概念—质点反应。质点反应的定义是:在a球上作用一个变化速度较大的力，使得b球运动后滞于a球的运动，这时，b球后滞于a球运动的时间称为质点反应。

质点反应的大小与杆的抗侧移刚度、b球的质量有关。杆的抗侧移刚度越大，质点反应就越小。b球的质量越大，质点反应就越大。让我们观察一下弹性单摆的运动规律，一个单质点与支座之间用一个弹簧片连接，我们给质点一个初始位移使之自由振动。质点由平衡位置至一侧最大位移，再经过平衡位置至另一侧最大位移，最后到平衡位置所需要的时间称为周期。那么，质点由平衡位置至最大位移所需要的时间是四分之一周期，这个四分之一周期是否是b球的后滞于a球运动的时间呢。换句话讲，质点的四分之一周期是否为质点反应呢，这个需要实验验证。现在，我们只有假定，质点反应的值为质点自由振动的四分之一周期。

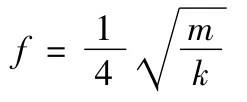
式中:f为质点反应;m为质点质量;k为杆抗侧移刚度。

4 质点反应的作用

有了质点反应的概念后，系统组成一个系统，在a球受力状态下为非刚体的条件是，力的变化速度在a球中产生位移所需要的时间与b球的质点反应相近。也就是说力的变化速度产生的效应接近b球的质点反应时，系统组成的系统为非刚体。力的变化速度产生的效应远离b球的质点反应时，系统组成的系统为刚体。

从上面分析可以看出，力的变化速度决定着一个系统是否为刚体，因此，力的第四要素是力的变化速度。

5 运动形态分析推广

前面的分析是建立在系统静止状态，经过分析，系统处于任何状态均可。无论系统处于什么状态，只要a球受变化的力，其速度发生变化，只要这个变化的力的效应接近b球的质点反应、且质点反应起作用，那么，b球的速度变化就后滞于a球的速度变化。

6 作用

力的第四要素有什么作用呢。力的三要素作用的对象是单体、单质点，因此，力的三要素研究的是单体、单质点静止或运动状态的力学关系及运动规律。力的三要素加上力的第四要素作用的对象是相关的双体。因此，力的四要素研究是相关双体的在质点反应起作用时的运动规律。若力的第四要素特别小，以致使质点反应不起作用，这时，系统为刚体，此时，其运动(状态)规律与力的三要素的规律无差异。

既然力的四要素是研究相关双体的运动规律，因此，凡是能简化为相关双体运动的问题，可用力的四要素去解决，如碰撞，爆炸，建筑物的地震反应。

7 结束语

由于作者没有实验的条件，本文未经实验证实，欢迎有实验条件的同行采用各种途径用实验验证力的第四要素。

［1］浙江大学理论力学教研室编.理论力学(第四版)［M］.北京:高等教育出版社，2009

［2］李卓球，朱四荣.工程力学［M］.武汉理工大学出版社，2008