基于改进粒子群优化算法的电子产品排产研究

祝 勇 潘晓弘

浙江大学，杭州，310027

基于改进粒子群优化算法的电子产品排产研究

祝 勇 潘晓弘

浙江大学，杭州，310027

针对以获得最大效益为目标的电子制造企业的订单生产安排问题，提出一种基于改进粒子群优化算法的电子产品排产方法，建立了模糊生产能力约束条件下的电子产品订单排产模型。在模糊生产能力约束条件下，该模型以由装配生产费用和拖期生产产生的惩罚费用所构成的总费用最小化为目标函数。为求解该排产模型，提出了一种动态改变惯性权重的粒子群算法，引入粒子群多样性和进化速度两个参数，并以此构造了动态改变惯性权重的计算式，从而可以更好地搜索问题解空间，避免了因粒子群多样性降低导致的粒子陷入局部极值的困扰。应用实例的计算分析表明了所提出方法的有效性。

电子产品排产；模糊约束整数规划；粒子群优化算法；自适应惯性权重

0 引言

近年来许多学者对订单排程的各种问题进行了大量的研究［1－5］，对多种生产情况下的基于优先级调度规则的生产调度与排程分别进行了论述。Leung等［1－2］研究了在满足订单交货期约束下，多产品在多机器上的生产调度。Lin等［4］、Wang等［5］都采用启发式方法来解决在一定约束条件下使订单总的加工或完成时间最短的问题。目前研究人员在生产调度方面做了很多相关工作［6－7］，但大多都只是从订单的完成日期或交货日期出发进行生产安排，或者只考虑成本，没有将两者综合考虑。

在实际生产过程中，很多时候不能作出精确决策，这时需要用模糊数来表示，例如产能在一定范围内浮动，可用三角模糊数来表示。在模糊产能约束条件下，考虑采用加工费用与拖期生产的惩罚费用之和为优化目标，建立模糊约束整数规划模型，该模型是一个多维复杂约束优化问题。为求解该问题本文提出一种新的自适应惯性权重粒子群优化算法（particle swarm optimization algorithm with dynamically changing weight，DCWPSO），基于粒子群多样性和进化速度动态改变惯性权重，最后通过一个实例验证了采用DCWPSO求解该订单排产模型是有效的。

1 问题描述与模型建立

1.1 参数描述

某电子制造企业有M条装配线，用Bi（i＝1，2，…，M）表示，生产N 种产品，用Pj（j＝1，2，…，N）表示。用矩阵A的元素~aij表示装配线Bi单位时间装配产品Pj的数量；用矩阵F的元素fij表示装配线Bi装配单位产品Pj所需的费用；用矩阵G的元素~gij表示单位产品Pj消耗装配线Bi的工时。~Hit表示装配线Bi在第t天时的模糊空闲时间（每天的空闲时间在一定范围内波动，因此用模糊变量表示）。生产的最小批量为b，并且假设零部件和原材料供应充足。

企业在计划期［0，T］（T为自然数）内接到L个客户订单，用Ok（k＝1，2，…，L）表示。订单Ok对产品Pj的需求量为Dkj，交货期用dk表示。

1.2 模糊约束整数规划排产模型

电子产品订单生产主要是面向装配，电子产品的利润较低，加工成本越低，企业能获得的利润越高。由于同一产品在不同装配线上的装配能力与费用是不同的，故不同的安排生产的方法所产生的加工费用不同。设第i条装配线Bi在第t天时加工第j个产品Pj的数量为xijt，则加工费用Cm为

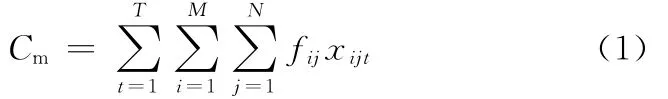
由于需求与可用装配生产能力不能完全匹配，企业经常会出现拖期生产，而拖期生产需要向客户支付惩罚费用，设Pj拖期生产的单位惩罚系数为vj。

设αkt为订单Ok在第t天时是否要交货函数，若是，则αkt为1，否则为0，即

优化目标是最小化加工费用与拖期惩罚费用之和，决策变量为第i个装配线Bi在第t天时加工第j个产品Pj的数量xijt，从而建立如下模糊约束整数规划模型：

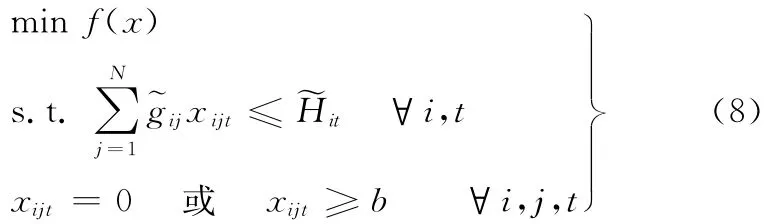
1.3 模糊生产能力约束的处理

对于式（6），由于生产能力的模糊性导致了约束的模糊。模糊生产能力~Hit采用三角模糊数（H（1）it，H（2）it，H（3）it）表示。

设装配线Bi在第t天时的负荷为

设ξ、η是两个模糊变量，则根据模糊变量的期望值比较原理［8］，有

根据式（10），当E（Git）≤E（~Hit）时，式（6）的约束条件满足。

2 改进粒子群优化算法求解

2.1 整数粒子群优化算法

对于式（8），由于模糊生产能力约束的存在，传统的数学规划方法不能求解，粒子群优化（particle swarm optimization，PSO）算法是由Kennedy等［9］和Eberhart等［10］提出的源于群智能的一种智能优化算法，它用无质量无体积的粒子作为个体，并为每个粒子规定简单的行为规则，从而使整个粒子群表现出复杂的特性，可用来求解复杂的优化问题。PSO算法有着个体数目少、计算简单、鲁棒性好等优点，在函数优化、模糊系统控制、组合优化、约束优化等领域均取得了非常好的应用效果［10］。

在标准PSO算法中，粒子通过下式更新自己的速度和位置：

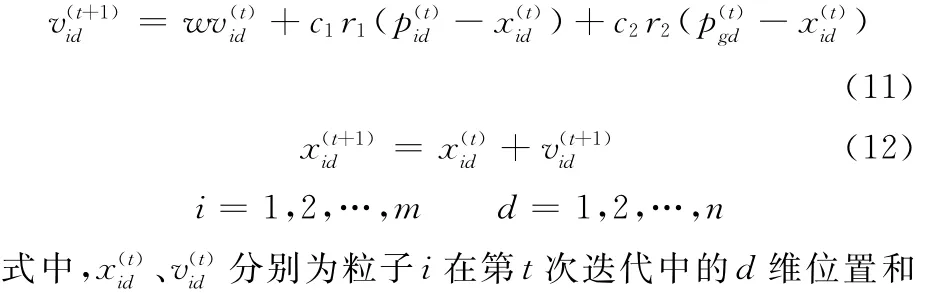
标准PSO算法在求解复杂多维约束优化问题（如订单排产模型）时存在早熟收敛现象并且容易陷入局部最优。

2.2 惯性权重的动态改变

在PSO算法的参数中，惯性权重是最重要的参数，较大的惯性权重有利于全局探索，而较小的惯性权重有利于算法的局部搜索，加速算法的收敛。本文在前人研究成果的基础上，提出了一种新的基于粒子群多样性和进化速度的自适应惯性权重调整方法，当进化速度快时，需提高全局搜寻能力，当粒子群多样性差时，此时粒子群的全局搜索能力较差，要使粒子尽快地进入全局搜索，此时需要增大惯性权重，反之减小惯性权重。

文献［9］采用下式改变惯性权重w：

惯性权重线性递减PSO算法（LDWPSO）在搜索后期由于多样性降低，粒子容易陷入局部最优。为了避免因粒子群多样性降低导致粒子陷入局部极值，引入粒子群多样性和进化速度两个参数。

粒子群多样性Dt为所有装配线在某时加工各产品数量的差异程度，可表示为平均聚集距离与最大聚集距离之比：

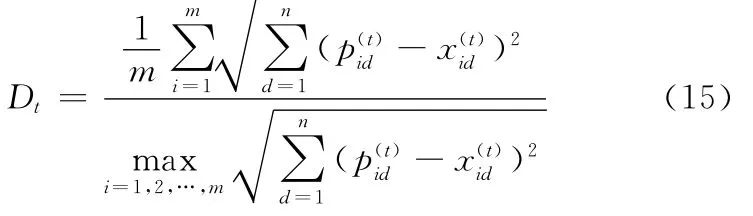
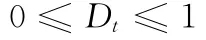
当粒子都处于同一点时，Dt定义为0，粒子群多样性最差。随着粒子的扩散，Dt增大，粒子群多样性变好。

搜索开始时，Et较小，进化速度较快，需扩大搜索空间，也即要w较大；随着搜索的进行，Et增大，进化减慢，这时要加强局部搜索能力，即要w较小。当Dt较小时，粒子群多样性较差，需要使其有扩展搜索空间的能力，即要w较大，相反，当Dt较大时，粒子群多样性较好，需要能更好地搜索局部最优解，即要w较小。从而基于Dt和Et，根据下式动态改变惯性权重w：

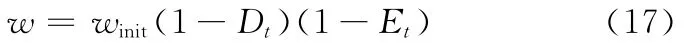
2.3 编码与约束处理机制

由于目标函数是最小化加工费用与拖期惩罚费用之和，所以可以直接采用目标函数作为适应值。订单排产模型中决策变量是正整数，编码可以采用解的自然表达，每个粒子表示的是各装配线在某个时间段上产品的生产情况，分量表示一条装配线上在某时生产一种产品的数量。从而一个粒子可以表示为：X ＝ ｛x111，x112，…，x11T；x121，x122，…，x12T；…；xMN1，xMN2，…，xMNT｝。

由于式（6）约束条件的存在，在粒子群进化搜索过程中，可能会产生无效解，需要对其进行修正，以保证粒子表示的是可行解。一个解xi的不可行度IF（xi）可表示为

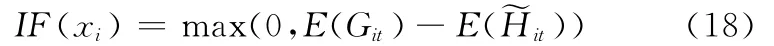
于是，当IF（xi）＞0时，式（6）不满足，否则满足。定义数组ISIF（m）记录粒子在迭代过程中是否满足生产能力约束（式（6）），若满足，则置为1，不满足，则置为0。

为了保证模糊生产能力约束能够被满足，在粒子生成和更新过程中的修复方程为

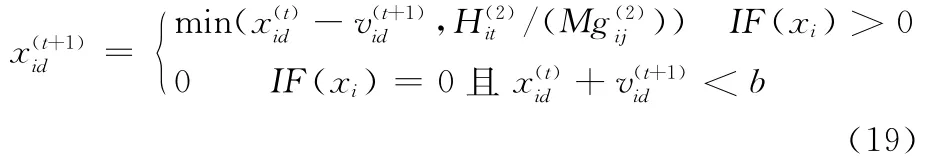
2.4 DCWPSO算法

DCWPSO算法随着搜索的进行，根据粒子群多样性Dt和进化速度Et动态改变惯性权重w，其具体步骤如下：

（1）设定粒子群的规模为m，维数为n，n＝MNT，最大迭代次数为tmax。

（2）初始化粒子的位置x为最小批量b和速度v。将粒子的个体最优值pi设为当前位置，pg设为初始化群体中最佳粒子的位置，置ISIF（m）＝1。

（3）计算粒子的适应度f（x）、个体最优值pi、全局最优值pg。

（4）判断算法收敛准则是否满足，如果满足，转步骤（8），否则执行步骤（5）。

（5）对粒子群中的所有粒子执行以下操作：①根据式（15）～式（17）计算粒子群多样性Dt、进化速度Et以及惯性权重w；②根据式（12）和式（13）更新粒子i的位置xi和速度vi；③ 根据式（18）计算xi的不可行度IF（xi），若IF（xi）＞0则置ISIF（xi）＝0。

（6）若ISIF（xi）＝0，则根据式（19）修正xi。

（7）迭代次数t加1，转步骤（3）。

（8）输出全局最优值pg，算法运行结束。

3 应用案例

某电子制造企业有4条装配线，生产6种产品。装配线的能力矩阵A和费用矩阵F分别为

计划周期［0，T］为［0，30］，各装配线的时间能力约束如表1所示，B1在第3、4、9、10、11、17、18天被占用；B2在第1、4、5、6、13、14、19、20天被占用；B3在第3、7、8、9、15、22、23天被占用；B4在第2、3、6、12、13、16、17、20、21天被占用。最小生产批量b＝100。

订单如表2所示，其中各订单Ok中对应产品Pj的需求量为Dkj，dk为订单Ok的交货期，vj＝｛1.5，1.2，1.4，1.3，1，1.2｝。

为了与惯性权重线性递减PSO算法［9］和文献［12］中的改进PSO算法（ACWPSO）相比较，本文算法（DCWPSO）与之采用同样的参数：粒子群规模为30，维数为4×6×30＝720，最大进化代数为500，c1＝c2＝2.0，winit＝1.2，wend＝0.4。仿真环境为 MATLAB 7.5，CPU Intel Pentium Ⅳ2.0G，内存2G，经过MATLAB仿真计算，DCWPSO耗时322s，LDWPSO 耗时406s，ACWPSO耗时354s，订单完成日期和费用如表3所示，仿真结果如图1所示。

表1 各装配线的时间能力约束 d

表2 计划期内客户订单需求

表3 三种算法下的订单完成日期、费用和耗时

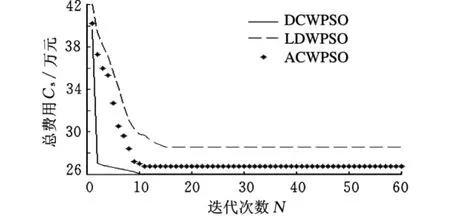
图1 DCWPSO、LDWPSO、ACWPSO排产结果比较

DCWPSO排产的最少加工费用与拖期惩罚费用之和为260 118元，其中加工费用Cm为221 362元，拖期生产惩罚费用Cl为38 756元，此时排产结果如表4所示。而采用LDWPSO排产时的总费用为285 627元，比采用DCWPSO排产时的总费用高了约9.8%，采用ACWPSO排产时的总费用为267 081元，比采用DCWPSO排产时的总费用高了约2.7%。DCWPSO收敛最快，耗时最少，为322s，LDWPSO耗时比DCWPSO增加了约26%，ACWPSO耗时比DCWPSO增加了约10%。由此可见，DCWPSO的最优解要优于LDWPSO和ACWPSO，其引起的总费用最少，但收敛速度更快，耗时更少，这在求解大规模问题时体现更明显。

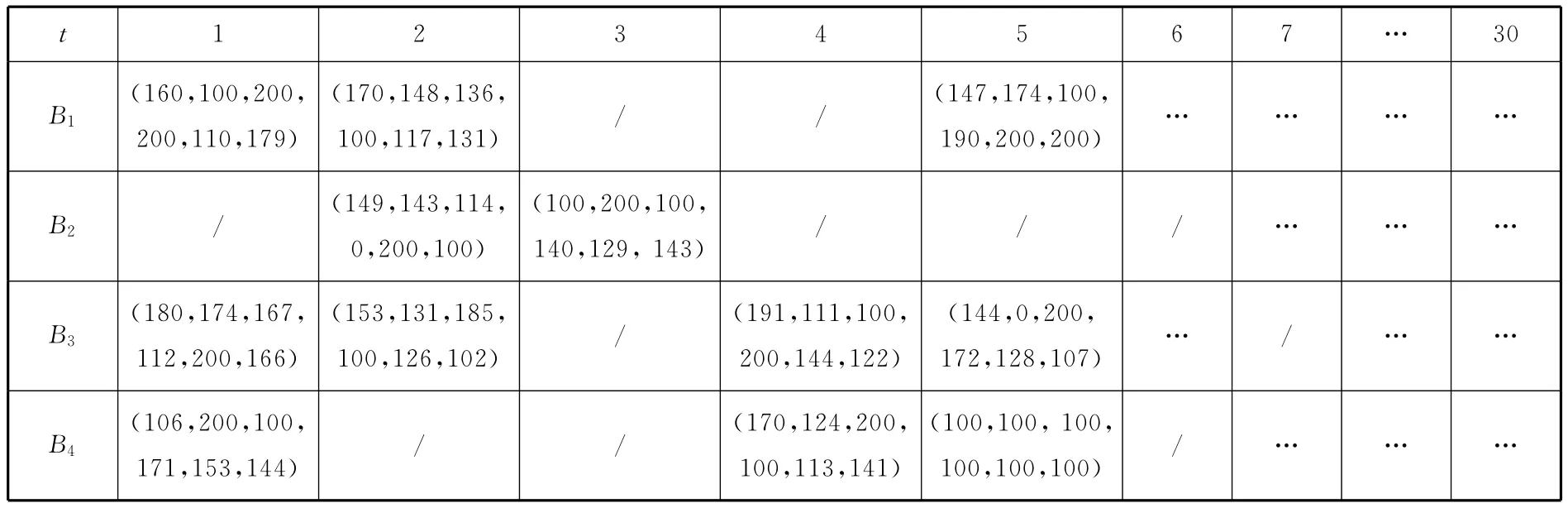
表4 各装配线的产品生产安排结果

4 结束语

本文提出了基于改进PSO算法的电子产品订单排产方法，建立了模糊约束整数规划的订单排产模型，通过改进PSO算法求解。基于粒子群多样性和进化速度动态改变惯性权重，以更好地搜索解空间，避免了因粒子群多样性降低而导致的粒子陷入局部极值的困扰，并且对于违反约束的粒子采用了修复技术，以防止不可行解的产生。仿真结果表明，对于复杂约束排产优化问题，DCWPSO算法寻优性能优良，为企业快速排产提供了一种新方法。不过此算法的收敛性理论分析还有待进一步研究。

［1］ Leung J Y T，Li H，Pinedo M.Scheduling Orders for Multiple Product Types with Due Date Related Objectives［J］.European Journal of Operational Research，2006，168（2）：370－389.

［2］ Leung J Y T，Li H，Pinedo M.Scheduling Orders for Multiple Product Types to Minimize Total Weighted Completion Time［J］.Discrete Applied Mathematics，2007，155（8）：945－970.

［3］ Li K，Ganesan V K，Sivakumar A I.Scheduling of Single Stage Assembly with Air Transportation in a Consumer Electronic Supply Chain［J］.Computers＆Industrial Engineering，2006，51（2）：264－278.

［4］ Lin B M T，Kononov A V.Customer Order Scheduling to Minimize the Number of Late Jobs［J］.European Journal of Operational Research，2007，183（2）：944－948.

［5］ Wang G，Cheng T C E.Customer Order Scheduling to Minimize Total Weighted Completion Time［J］.Omega－International Journal of Management Science，2007，35（5）：623－626.

［6］ 金锋，吴澄.大规模生产调度问题的研究现状与展望［J］.计算机集成制造系统－CIMS，2006，12（2）：161－168.

［7］ 徐俊刚，戴国忠，王宏安.生产调度理论和方法研究综述［J］.计算机研究与发展，2004，41（2）：257－267.

［8］ Liu B，Liu Y K.Expected Value of Fuzzy Variable and Fuzzy Expected Value Models［J］.IEEE Trans.on Fuzzy Systems，2002，10（4）：445－450.

［9］ Kennedy J，Eberhart R C.Particle Swarm Optimization［C］／／Proc.of 1995IEEE Int.Conf.on Neural Network，Ⅳ.Piscataway：IEEE Service Center，1995：1942－1948.

［10］ Eberhart R C，Shi Y.Particle Swarm Optimization：Developments，Applications and Resources［C］／／Proc.of 2001IEEE Int.Conf.on Evolutionary Computation.Piscataway：IEEE Service Center，2001：81－86.

［11］ Eberhart R C，Shi Y.A Modified Particle Swarm Optimizer［C］／／Proc.of 1998IEEE Int.Conf.on Evolutionary Computation.Piscataway：IEEE Service Center，1998：69－73.

［12］ 王启付，王战江，王书亭.一种动态改变惯性权重的粒子群优化算法［J］.中国机械工程，2005，16（11）：945－948.

Scheduling Electronic Products Based on a Modified Particle Swarm Optimization

Zhu Yong Pan Xiaohong
Zhejiang University，Hangzhou，310027

Order－oriented production was satisfied to maximizing the profit，and to the due date of customer order.In such a circumstances，scheduling orders had been an important decision in modern enterprises.A method of scheduling electronic products based on a modified PSO was proposed.A cost model of scheduling orders for electronic products with fuzzy capacity constraints was established.The total cost was constituted of two costs，they were production costs from the assembly and penalty cost arising from tardiness production.A new adaptive particle swarm optimization algorithm with dynamically changing inertia weight（DCWPSO）was proposed to solve the problem.The DCWPSO changed inertia weight based on population diversity and evolution speed in order to balance the trade－off between exploration and exploitation.The application demonstrates the efficiency of the proposed model and DCWPSO algorithm，which is significantly superior to the linearly decreasing weight PSO （LDWPSO）in convergence speed and accuracy.

scheduling electronic product；integer programming with fuzzy constraint；particle swarm optimization（PSO）algorithm；adaptive inertia weight

F273；TP391

1004—132X（2011）01—0049—06

2010—01—28

国家高技术研究发展计划（863计划）资助项目（2009AA04Z151，2007AA040607）

（编辑 王艳丽）

祝 勇，男，1979年生。浙江大学现代制造工程研究所博士研究生。主要研究方向为生产管理、供应链管理、制造业信息化等。发表论文6篇。潘晓弘，男，1954年生。浙江大学机械工程学系教授、博士研究生导师。