负剩余价值和正利润可以同时存在吗?——破解斯蒂德曼的联合生产之谜

冯金华 侯和宏

一、引言

根据马克思主义经济学基本原理,一个显而易见的事实是:如果一个社会存在平均利润,则一定有剩余价值。其理由几乎是不证自明的,因为根据定义,平均利润本来就是剩余价值在社会总资本中进行平均分配而得到的结果。从总量上说,二者实际上是一回事。这个事实后来被置盐信雄(N.Okishio)概括为“马克思基本定理”。[1]根据这个定理,正的剩余价值是正的平均利润存在的充分必要条件。换句话说,如果剩余价值大于零,则平均利润就一定大于零,反之,如果平均利润大于零,则剩余价值也一定大于零。

令人奇怪的是,这个定理后来在西方经济学界却受到诸多质疑。英国经济学家斯蒂德曼(I.Steedman)就是这些质疑者中影响较大的一位。他在1977年出版的《按照斯拉法思想研究马克思》一书中专设了一章,标题就叫“剩余价值为负时的正值利润”。[2](P129)在这一章中,斯蒂德曼以举例的方式说明,在联合生产的情况下,价值和剩余价值既可以为正,也可以为负,特别是,当剩余价值为负时,平均利润却可以为正,此外,当剩余价值为正时,平均利润也可以为负。他由此得出结论说:“在进行联合生产时,如果采用马克思的价值定义,对于正的利润的存在而言,剩余价值为正既不是必要条件也不是充分条件。”[3](P133)“因此,马克思用价值=C+V+S的计算方法定义的价值概念应当予以摒弃。”[4](P129)

自然地,斯蒂德曼对马克思基本定理的质疑本身也立刻就受到了质疑。争论主要集中在三个方面。首先,斯蒂德曼使用的方法是否正确?森岛通夫(Morishima)认为斯蒂德曼用投入产出方法来描述联合生产是不恰当的,因为联合生产涉及最优化问题。受冯·纽曼(J.V.Neumann)的一般动态经济均衡模型[5](P1-9)的启发,森岛通夫指出应当用“黄金规则”不等式来描述联合生产[6](P387-391)。其次,斯蒂德曼假设的前提是否恰当?库茨(Heinz D.Kurz)认为斯蒂德曼没有考虑到资本主义的竞争和剥削,没有对资本主义的生产关系和生产性质作出分析。[7](P52-70)法因(Emmanuel Farjoun)认为在斯蒂德曼的例子中存在两个不同效率的生产过程,第一个生产过程的效率要低于第二个生产过程的效率,这与资本主义竞争经济均衡相违背。因为资本主义的竞争必然淘汰没有效率的生产过程,因此不可能同时出现两种不同效率的生产过程的联合生产。[8](P115)中国的许多学者也围绕这个问题提出了自己的意见。白暴力认为,斯蒂德曼的假设只适用于自然经济。理由是在模型的两个生产过程中,每一个都同时生产两种商品,这相当于假定社会生产中的每一个生产过程都生产社会经济中的所有产品。这与现代社会大生产的分工事实相违背。另外,斯蒂德曼使用的是实物价格理论,不仅不能说明价格的本质,而且更不能说明资本主义生产过程中的剥削关系。[9](P67-71)丁堡骏认为斯蒂德曼的例子具有随意性,没有反映现实生活。[10](P2)第三,斯蒂德曼对模型的解法是否成立?伊藤诚(M.Itoh)认为联合生产问题不能通过简单的联立方程组来求解。伊藤诚的解决方案是,联合生产过程中产品价值的决定取决于生产领域内的价值规律和流通领域内的价值规律的共同作用。先是生产领域内的价值规律决定联合生产过程中的两种产品的价值总和,然后再通过流通领域内的价值规律——由货币表现出的全社会对两种商品购买力的变化之比——来决定每一种产品的价值量。[11](P155-157)

然而,可惜的是,在所有这些批评中,很少有人看到,斯蒂德曼的模型和他的价值体系之间存在着深刻的矛盾和严重的错误,即它从根本上违背了社会必要劳动时间决定商品价值量的原理。斯蒂德曼对马克思基本定理、对马克思劳动价值论和剩余价值论的全部诘难都是建立在这些矛盾和错误的基础之上的,因而是完全没有道理的。

本文首先简要地概述斯蒂德曼为反驳马克思基本定理而建立的模型。为避免引起误解,我们将原封不动地采用斯蒂德曼原书中的数字例子,然后讨论该模型的错误所在,说明应当如何按照马克思的劳动价值论特别是社会必要劳动时间决定商品价值量的原理来分析所谓的联合生产。本文的结论是:一旦根据社会必要劳动时间决定商品价值量的原理来确定联合生产中劳动所形成的价值,就不可能出现所谓负的价值和剩余价值,因而,也就不可能出现负剩余价值与正利润(或者正剩余价值和负利润)共存的现象。

二、斯蒂德曼之谜

斯蒂德曼的基本假定包括:在一个社会中只存在两种生产过程(生产过程1和生产过程2),生产两种商品(商品1和商品2)。每种生产过程都使用某种商品和劳动来同时生产两种商品,即是所谓的联合生产,且所有的投入都在一个生产时期中被全部消耗掉。此外,每种生产过程都具有规模报酬不变的性质。

根据上述假定,斯蒂德曼设计了如下的数字例子(参见表1):生产过程1使用5个单位的商品1和1个单位的劳动,生产出6个单位的商品1和1个单位的商品2;生产过程2使用10个单位的商品2和1个单位的劳动,生产出3个单位的商品1和12个单位的商品2。两个生产过程总共使用5个单位的商品1、10个单位的商品2和2个单位的劳动,生产出9个单位的商品1和13个单位的商品2。

表1 联合生产(斯蒂德曼模型)

斯蒂德曼进一步假定,在两个生产过程中,每单位劳动形成或创造的价值都等于1,并设商品1和商品2的单位价值分别为L1和L2。于是,表1用实物形式表示的两个生产过程就可以分别表示为如下的两个方程:

其中,每个方程的等号两边分别是相应生产过程的投入价值和产出价值。

方程(1)和(2)是斯蒂德曼的相应于表1的价值体系。解之即得L1=-1、L2=2。这里,商品1的价值为负。于是,斯蒂德曼得出结论说:“在出现联合生产的场合,马克思的价值计算方法会使任一种商品既可能具有正的价值,又可能出现负的价值。”[12](P138)

借助上面求得的商品1和商品2的价值以及由表1最后一行所表示的总生产过程,斯蒂德曼接着讨论了整个社会的总产值W、不变资本C、可变资本V和剩余价值S。

由表1的最后一行容易看出,总产值和不变资本分别为:

为了求出可变资本,斯蒂德曼假定,1单位劳动的实际工资为3/6个单位的商品1和5/6个单位的商品2。于是,总工资即可变资本为:

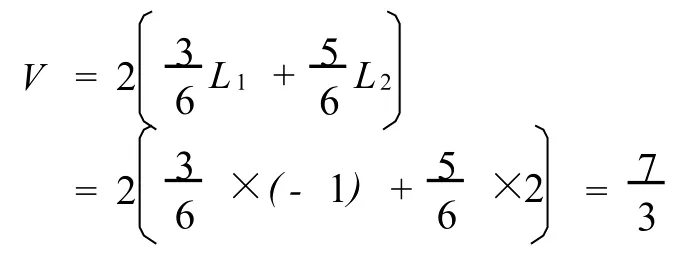
最后,总剩余价值等于总产值减去不变资本和可变资本,即:

于是,斯蒂德曼又得出结论说:在联合生产的条件下,不仅商品的价值可能是负的(如上述的商品1),而且,剩余价值也可能是负的!

现在来看斯蒂德曼的价格体系。斯蒂德曼认为,若假定劳动的价格和价值一样也为1,并用P1和P2分别表示商品1和商品2的价格,用r表示整个社会的平均利润率,则下面两个关系式必定成立:

由于(3)和(4)两个方程包含了r、P1和P2三个未知数,不能求得确定的解,故斯蒂德曼又增加了一个方程:

他的理由是:“由6单位劳动购买的实际工资品组合必须能支配6单位劳动”[13](P131)。

方程(3)、(4)和(5)是斯蒂德曼的相应于表1的价格体系。解之即得①还有一个解因为包括了负价格而被略去。:

由于在这个解中,所有的变量都是正的,特别是,其中的平均利润率(从而平均利润)也是正的,而前面在解价值体系时得到的剩余价值却是负的,故斯蒂德曼确信他最终证明了:在联合生产的条件下,即使剩余价值为负,平均利润也可以为正!

三、谜的破解

在斯蒂德曼的价值体系中,为什么会出现负的价值和剩余价值呢?破解这一谜团的关键是要认识到,斯蒂德曼在决定劳动所创造的价值时使用的是“个别时间”或“自然时间”,而不是马克思所说的“社会必要劳动时间”。例如,在表1中,斯蒂德曼假设投入两个生产过程的劳动都是1个单位的自然时间,而在由表1转化而来的价值体系即方程(1)和(2)中,每1单位自然时间的劳动都形成了1单位的价值。这是斯蒂德曼价值体系的根本错误所在。②顺便说一下,斯蒂德曼的价格体系也有很多错误,如可变资本没有参加利润的平均化等。

下面我们把社会必要劳动时间决定商品价值量的原理首先运用于分析斯蒂德曼的联合生产,然后运用于分析他没有考虑过的其他类型的联合生产,最后运用于分析一般形式的联合生产。所得到的结果都是:只要按照社会必要劳动时间来决定价值量,则不仅在斯蒂德曼的联合生产模型中,而且在所有其他类型的联合生产模型中,都不可能出现负的剩余价值以及负剩余价值和正利润同时并存的现象。

(一)斯蒂德曼的联合生产

按照马克思的劳动价值论,在生产相同商品的同一行业或同一部门的内部,不同生产过程(如不同企业)的劳动所创造的价值是由社会必要劳动时间(而非自然时间)决定的。同样1单位劳动所创造的价值,在效率较高的生产过程中要比在效率较低的生产过程中更大。因此,如果两个生产过程中的劳动具有不同的效率,则相同自然时间的劳动所创造的价值就不会相同。这是马克思劳动价值论的一个基本原理。

例如,假设某个行业只有两个生产过程,生产同一种商品,即是所谓的非联合生产。生产过程1用1小时生产了1件商品,但生产过程2用1小时却生产了3件商品(为简单起见,这里不考虑生产中的转移价值部分),即生产过程2的单位劳动的净产出是生产过程1的3倍,或者说,生产过程2和生产过程1的单位劳动净产出之比等于3。①单位劳动的净产出等于总产出减去全部的物质消耗再除以劳动量。由于两个生产过程总共用了2个小时生产了4件商品,故每件商品中包含的社会必要劳动时间是0.5个小时。这样,生产过程1的1个小时创造的价值是0.5×1=0.5,生产过程2的1个小时创造的价值是0.5×3=1.5,即生产过程2的1小时劳动所创造的价值是生产过程1的3倍。换句话说,当生产过程2与生产过程1的单位劳动的净产出比等于3时,相应的价值之比也等于3。若用λ来表示生产过程2与生产过程1的单位劳动所创造的价值之比(简称生产过程2的价值比率),则有:

尽管上面讨论的是非联合生产的情况,但显而易见,社会必要劳动时间决定商品价值量的原理也同样适用于联合生产。一旦将这一原理运用于联合生产,所谓的斯蒂德曼之谜立刻就会被破解。与此同时,在很长一段时间中一直存在的关于马克思的劳动价值论是否适用于联合生产的种种疑虑也会被一扫而光。

首先我们看到,在斯蒂德曼的表1中,两个生产过程生产的都是同样的联合商品,即都是既生产商品1,也生产商品2。因此,从本质上说,它们属于同一个行业或同一个部门,是同一行业内部的两个不同的生产过程。这意味着,我们完全可以把社会必要劳动时间决定商品价值量的原理运用于斯蒂德曼的联合生产。

其次,在斯蒂德曼的两个生产过程中,劳动具有完全不同的净产出。②如前所述,法因曾经指出过,在斯蒂德曼模型中,两个生产过程具有不同的效率。但可惜的是,他没有进一步去分析这些不同的效率对劳动所创造的价值的影响。例如,在生产过程1中,1单位劳动的净产出是1(=6-5)个单位的商品1和1个单位的商品2;在生产过程2中,1单位劳动的净产出是3个单位的商品1和2(=12-10)个单位的商品2。参见表2。

表2 单位劳动的净产出(斯蒂德曼模型)

由表2可见,生产过程2的劳动的效率要高于生产过程1。我们可以从商品1和商品2两个方面来分析这个问题:生产过程2中单位劳动的净产出在只看商品1时是生产过程1的3倍,在只看商品2时是生产过程1的2倍。因此,将商品1和商品2放在一起看时,生产过程2的单位劳动的“综合”净产出应当是生产过程1的2到3倍。这意味着,根据社会必要劳动时间决定商品价值量的原理,生产过程2的单位劳动所创造的价值也应当是生产过程1的2到3倍。换句话说,如果假设生产过程1的1单位劳动所创造的价值为1,则生产过程2的1单位劳动所创造的价值就不应为1(像斯蒂德曼假定的那样),而是应当大于2但小于3。

在联合生产条件下,由于每个生产过程都同时生产两种商品,生产过程2与生产过程1的单位劳动的净产出比不再像非联合生产时那样只有一个,而是有两个,相应地,生产过程2的价值比率λ也不能再像非联合生产时那样等于那个唯一的净产出比,而必须要由全部的两个净产出比来共同决定。特别是,它必须位于由两个净产出比构成的“区间”之内。具体到表1或表2来说就是:净产出比区间为(2,3),价值比率λ∈(2,3)。至于λ到底为何值,即处在净产出比区间的哪一点,与我们目前讨论的问题无关。①实际上,社会必要劳动时间决定商品价值量的原理可以用来进一步确定λ的具体数值。关于这个问题,或者更一般地,关于联合生产中的价值决定问题,我们将另文专论。我们这里所要说明的是:只要按照社会必要劳动时间决定商品价值量的原理来确定生产过程2的劳动所创造的价值,即令生产过程2的价值比率位于它的净产出比区间之中,则所有商品的价值以及整个社会的剩余价值就不可能为负数。如果出现了负的价值,那一定是生产过程2的价值比率被定在了它的净产出比区间之外,而这恰恰违背了马克思的劳动价值论。

现在假定在表1中生产过程1的1单位劳动所创造的价值仍然为1②生产过程1的劳动所创造的价值可以任意给定,只要大于0即可。不过,如果给定的不是1而是其他数字,则生产过程2的劳动所创造的价值以及所有商品的价值都会发生同比例的变化。,但令生产过程2的1单位劳动所创造的价值由它的净产出比区间(2,3)决定并位于该区间之内,例如为2.45。于是,相应的价值体系为:

解之可得:L1=0.45、L2=0.55,即所有商品的价值均为正数。

容易验证,生产过程2的1单位劳动所创造的价值如果被定在小于2,则商品1的价值将为负数(但商品2的价值为正数);如果被定在大于3,则商品2的价值将为负数(但商品1的价值为正数)。此外,如果令它等于2,则商品1的价值为0(商品2的价值为1);如果令它等于3,则商品2的价值为0(商品1的价值为1)。这就表明,斯蒂德曼的负价值是违背社会必要劳动时间决定商品价值量原理(即让生产过程2的价值比率位于净产出比区间之外)的结果。

当L1=0.45、L2=0.55时,相应的社会总产值、总不变资本、总可变资本和总剩余价值分别为:

由此可见,同样是在联合生产的情况下,只要按照社会必要劳动时间决定商品价值量的原理来确定劳动所创造的价值,即令价值比率位于相应的净产出比区间之内,则不仅所有商品的价值必然为正数,而且,剩余价值也必然为正数。

在上面的讨论中,我们是通过令λ=2.45而得到所有价值和剩余价值都大于零的结果的。但如前所说,在这种情况下,令λ为任何大于2而小于3的数,都能得到同样的结果。

例如,我们解如下的价值体系:

解方程组得到L1=λ-2、L2=3-λ。这意味着,当2＜λ＜3时,一定有L1＞0且L2＞0,即两种商品的价值均为正。如果λ＞3,则商品2的价值为负;如果λ＜2,则商品1的价值为负。这就是前面讨论过的斯蒂德曼价值体系中的情况。

用L1=λ-2、L2=3-λ来计算社会总产值、总不变资本、总可变资本和总剩余价值的结果为:

因此,若要剩余价值大于零,只需要λ＞6/5。由此可见,当2＜λ＜3时,不仅所有商品的价值均为正,而且,剩余价值也为正。从这里可以看到,使剩余价值为正的条件要比使价值为正的条件更加宽松一些,因为2＜λ＜3意味着λ＞6/5,但反之则不然。

值得再次强调的是:我们的价值体系(6)和(7)与斯蒂德曼的错误的价值体系(1)和(2)的区别仅仅在于,我们把第二个方程等号左边的第二项由原来不符合马克思劳动价值论要求的1改成了符合马克思劳动价值论要求的位于相应净产出比区间(2,3)之中的2.45。正是由于这一小小的改动,使得负价值和负剩余价值的“幽灵”不再出现。因此,与斯蒂德曼所说的正好相反,负的价值和负的剩余价值不是“按照马克思计算价值的方法”得到的,而是违背它的结果。因此,在斯蒂德曼之谜中陷入困境的不是马克思,而是斯蒂德曼自己。

(二)其他类型的联合生产

以上所有的讨论都是围绕着斯蒂德曼模型即表1展开的。但表1给出的只是一个特殊的联合生产例子。在这个例子中,与生产过程1相比,生产过程2的劳动在两种商品上都有较高的效率,但效率高出的程度并不一样,即它的两个净产出比都大于1但不完全相同。然而,除此之外,还有两种不同的联合生产情况也需要讨论。第一种情况是:生产过程2的劳动仅仅在一种商品上有较高的效率,而在另一种商品上有较低的效率,即它的单位劳动的净产出比在某一商品上大于1,但在另一商品上却小于1。第二种情况是:生产过程2的劳动在两种商品上都有较高(或较低)的效率,但效率高出(或低出)的程度完全一样,即它的单位劳动的净产出比在两种商品上都大(小)于1且完全相同。通过对这两种情况的讨论可以进一步看到,负的价值和剩余价值以及负剩余价值与正利润并存的现象,不仅在斯蒂德曼的联合生产中不可能存在,而且在其他类型的联合生产中也不可能存在。

首先来看第一种情况。为明确起见,假定生产过程2的劳动在商品2上有较高的效率,但在商品1上有较低的效率。参见表3。

表3 联合生产(相反的净产出比)

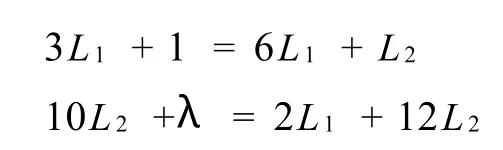
根据表3可建立如下方程组:这里,生产过程1的1单位劳动所创造的价值仍然假定为1,生产过程2的1单位劳动所创造的价值则假定为λ。从中解得:

于是,使商品价值均为正数的条件为2/3＜λ＜2。

为什么是这个条件呢?因为:由表3可知,与生产过程1相比较,生产过程2的单位劳动的净产出比在商品1上为2/(6-3)=2/3,在商品2上为(12-10)/1=2,即净产出比区间为(2/3,2),从而,生产过程2的价值比率λ∈(2/3,2)。这就是不等式2/3＜λ＜2的含义。

其次,来看第二种情况。例如,假定生产过程2的劳动在两种商品上都有较高的效率,但效率高出的程度完全一样。换句话说,它的两个净产出比完全相同,于是,净产出比区间“退化”为一个点。参见表4。

表4 联合生产(相等的净产出比)

与表1相比,表4只对生产过程2的产出数字稍稍做了改动:与以前一样,生产过程2使用了10个单位的商品2和1个单位的劳动,但却生产出2个单位的商品1和12个单位的商品2。通过这一改动,生产过程2的单位劳动的净产出分别为2个单位的商品1和12-10=2个单位的商品2,正好都是生产过程1的单位劳动净产出的2倍。在这种情况下,等量劳动在生产过程2中创造的价值自然是生产过程1的2倍。因此,如果假定生产过程1的1单位劳动创造的价值为1,则生产过程2的1单位劳动所创造的价值就是2。于是得到如下的方程组:

但是,该方程组其实就是一个方程,即1=L1+L2。这个方程意味着,1单位劳动的净产出是1单位的商品1加上1单位的商品2。

现在的问题是:在这种情况下,商品的价值有可能出现负数吗?回答仍然是否定的。尽管从方程1=L1+L2本身暂时还看不出这一点,但却可以借助于求“极限”的过程来寻找结果。方法如下:先稍微改动一下表4中的数字,使得相对于生产过程1而言,生产过程2的两个净产出比不再完全一致。例如,令生产过程2生产的商品2不是12个单位,而是12.1个单位。这样,它的净产出比区间就为(2,2.1)。再令生产过程2的价值比率λ在净产出比区间(2,2.1)中取某个值,例如取中间值2.05(取任何其他值都一样)。于是得到方程组:

容易解出相应的价值为L1=0.5、L2=0.5。①由1=L1+L2的对称性质容易猜想到有L1=L2=0.5。实际上,也可以严格地证明这个结果。

继续改动表4中的数字,让净产出比区间进一步缩小。例如,令生产过程2生产的商品2从12.1减少到12.01,即使净产出比区间缩小到(2,2.01),再让λ取该区间的中间值即2.005,于是方程组为:

它的解仍然为L1=L2=0.5。由此可以想到,如果按照上述方法一直进行下去,即使得净产出比区间的长度趋向于0,同时让λ总是位于净产出比区间的中点,则一直都会有L1=L2=0.5的结果。这样,我们便可以作出推论:即使两种生产过程的劳动效率的差别程度完全一致,商品的价值也不可能变为负数。

一个有趣的事实是,在表4给出的例子中,生产过程2的1单位劳动所创造的价值必须是2,即必须是生产过程1的劳动所创造的价值的2倍,否则,方程组就无解。例如,令生产过程2中1单位劳动所创造的价值为λ,则方程组变为:

由第一个方程可解得L1=1-L2,代入第二个方程后得到λ=2。

(三)一般形式的联合生产

以上讨论可以进一步推广到更加一般的联合生产中去。参见表5。假定生产过程1使用a1个单位的商品1、b1个单位的商品2和x1个单位的劳动,生产出c1个单位的商品1和d1个单位的商品2;生产过程2使用a2个单位的商品1、b2个单位的商品2和x2个单位的劳动,生产出c2个单位的商品1和d2个单位的商品2。相应的单位劳动的净产出则如表6所示。

表5 联合生产(一般模型)

表6 单位劳动的净产出(一般模型)

这里,单位劳动的净产出(矩阵)为:

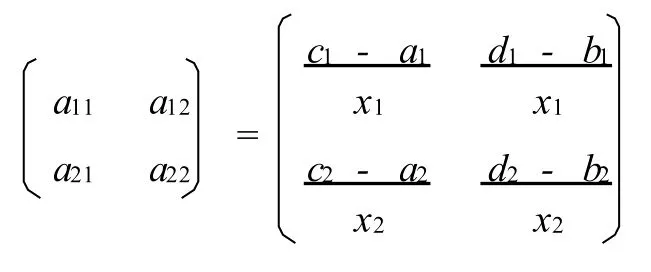
为简单起见,假定所有的净产出都不为零,即aij≠0,i,j=1,2,以及a22/a12≠a21/a11,即生产过程2在两种商品上的净产出比不完全相同。

由表6可知,相对于生产过程1来说,生产过程2的单位劳动的净产出比在商品1上为a21/a11,在商品2上为a22/a12,从而,净产出比区间为(a22/a12,a21/a11)(假定a22/a12＜a21/a11),从而,生产过程2在两种商品上的综合的净产出比或价值比率λ∈(a22/a12,a21/a11)。因此,若令生产过程1的单位劳动所形成的价值为1,则生产过程2的单位劳动所形成的价值就为λ。

与表6相应的价值体系是:

其解为:

利用上述方式(亦即斯蒂德曼所说的“马克思计算价值的方式”)来确定联合生产中劳动所形成的价值,并建立相应的价值体系,即可以保证所计算得到的商品价值和剩余价值都是正数。由此可见,按照社会必要劳动时间决定商品价值量的原理,即使是在联合生产的情形下,也不会产生负的价值和负的剩余价值,从而,也就不可能出现负的剩余价值和正的利润并存的奇怪现象。换句话说,如果斯蒂德曼真的“按照马克思的价值计算方法”来计算,就不会推导出负剩余价值以及负剩余价值与正利润并存这样一个怪胎。

四、结论

从以上分析可以看到,在斯蒂德曼的联合生产模型和价值体系之间,存在一个深刻的矛盾:一方面,在他的联合生产模型中,本质上属于同一行业的不同生产过程的单位劳动具有不同的净产出,即具有不同的效率;另一方面,在他的价值体系中,这些具有不同效率的单位劳动却创造出同样数量的价值。这就从根本上违背了马克思的劳动价值论,特别是违背了社会必要劳动时间决定商品价值量的原理。正是这一矛盾的存在,导致斯蒂德曼的价值体系出现所谓负的价值和剩余价值,导致出现负剩余价值和正利润并存的奇怪现象。尽管斯蒂德曼一再声称,他是按照“马克思所定义的商品价值和剩余价值”及“马克思的价值=C+V+S的计算方法”得出自己的结论的,但我们从他的价值体系中看到的事实却正好相反:他既没有正确地理解马克思的价值定义,也没有正确地运用马克思的计算方法。实际上,一旦我们真正运用马克思的劳动价值论来分析斯蒂德曼的联合生产模型,并完全按照社会必要劳动时间决定商品价值量的原理来确定不同生产过程中单位劳动的价值比率,那么,那些神秘的负价值和负剩余价值就会统统消失,而负剩余价值与正利润并存的怪事也将不复存在。换句话说,即使是在联合生产的情况下,价值和剩余价值也不可能为负数,从而更谈不上负剩余价值与正利润的并存。

[1]Okishio,N.“A Mathematical Note on Marxian Theo rems”.Weltw irtschaftliches A rchiv,1963,91:287-299.

[2][3][4][12][13]斯蒂德曼:《按照斯拉法思想研究马克思》,北京,商务印书馆,1991。

[5]Neumann,J.V.“A Model of General Economic Equilibrium”.The Review of Econom ic Studies,1945—1946,13(1):1-9.

[6]Mo rishima.“Marx's Economics:A Comment on CC.Von Weizsacker's A rticle”.Econom ic Journal,1974,84:387-391.

[7]Kurz,Heinz D.“Sraffa after Marx”.Australian Econom ic Papers,1979,18(June):52-70.

[8]Farjoun,Emmanuel.“The Production of Commodities by Meansof What?”.in Mandel and Freeman(eds.).Ricardo,M arx and Sraffa:the Langston M emorial Volume Introduced by Ernest M andel.The Langston Memo rial Volume.London:Verso,1984.

[9]白暴力:《实物价格理论分析》,载《学术研究》,2007(4)。

[10]丁堡骏:《按照马克思思想研究斯拉法——答斯蒂德曼》,载《税务与经济》,2003(1)。

[11]伊藤诚:《联合生产:斯蒂德曼遗留的问题》,载斯蒂德曼、斯威齐编:《价值问题的论战》,北京,商务印书馆,1990。