基于区域网平差的InSAR基线估计方法

靳国旺,吴一戎,向茂生,徐 青,秦志远

1.中国科学院电子学研究所 微波成像技术国家级重点实验室,北京 100190;2.信息工程大学 测绘学院,河南 郑州450052

1 引 言

合成孔径雷达干涉测量[1-3](interferometric synthetic aperture radar,InSAR)技术在地形测绘[2-3]、地表形变监测[4]、冰川运动研究[5-6]等方面都表现出快速、高精度、全天时、全天候、大区域等突出优势[2-3],已经成为目前发展迅速、极具潜力的对地观测及测绘新技术之一。

利用InSAR技术快速获取高精度数字高程模型 (digital elevation model,DEM)是目前InSAR应用研究的一个主要方面。在 InSAR处理中,基线估计或干涉参数定标是关键步骤之一,其精度直接影响最后获取高程的精度。

在干涉参数定标方面,文献[7]建立了考虑多路径效应等参数的定标模型,文献[8—9]介绍了基于敏感度方程的干涉定标方法,文献[10]针对SRTM设计了利用点目标及分布式目标进行辐射定标和相位定标的方案,文献[11]介绍了GeoSAR P波段的干涉定标情况,文献[12]基于敏感度矩阵的条件数研究了机载InSAR定标模型和定标器布放问题,文献[13]介绍了一种InSAR地理编码和镶嵌系统,文献[14]等介绍了大区域SAR数据生成DEM的平差方处理方法。

为了提高基线估计的精度和可靠性,作者对机载双天线InSAR系统的基线参数估计方法进行了研究,并提出了一种新的干涉参数定标模型[15]。为了利用少量地面控制点完成大面积、多套InSAR数据的基线估计,在文献[15—16]的基础上,设计了考虑干涉相位偏置的区域网平差基线估计方法。

在进行大面积、多套InSAR数据的基线估计时,如果不考虑各干涉数据之间的连接条件而采用各像对单独基线估计方法,将存在以下问题:①对于每对干涉数据,都需要足够数量、分布合理的地面控制点来完成基线估计,在整个大区域内完成所有干涉像对的干涉处理和数字高程模型及正射影像的获取工作就需要获取大量、分布合理的地面控制点,需要消耗大量的人力和财力;②由于基线估计误差的存在,在各套干涉数据接边处反演的高程值之间将存在较大差异,不同干涉数据获取的DEM及正射影像之间将存在较大的相对误差。综上所述,采用各套数据单独基线估计方法,很难以经济、高效的方式完成大面积地形测绘工作。

在光学图像的摄影测量和SAR立体图像的摄影测量中,经常采用区域网平差思想由少量地面控制点加密出测图用的大量控制点。为了促进InSAR技术在大面积地形测绘中的实用化,笔者引入区域网平差思想,提出一种考虑干涉相位偏置的区域网平差InSAR基线估计方法。

2 基于区域网平差的基线估计原理

令 R表示主天线相位中心到相应地面点的斜距,ΔR表示InSAR成像时两天线相位中心到同一地面点的斜距差,B表示两天线相位中心之间的基线长度,α表示基线与水平方向的夹角,H为天线相位中心的高程,h为地面点的高程。则由InSAR的基本原理[3]可得到如下关系式

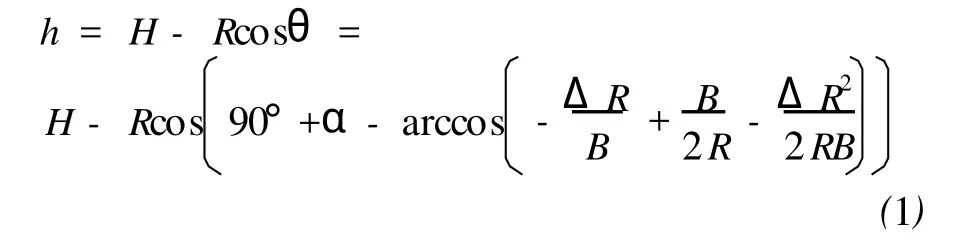
对式(1)进行变换,可得

式(2)可简记为

当考虑误差因素影响时,可将式(3)对基线长度、基线水平角和干涉相位偏置三个参数及高程值h线性化后得到误差方程

其系数分别为

常数项为

式(4)写成矩阵形式为

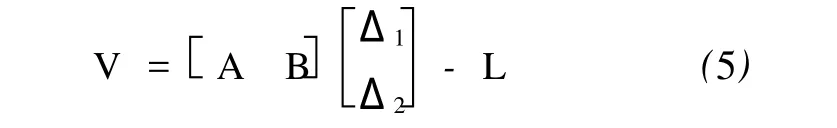
为了简要说明考虑干涉相位偏置的区域网平差基线估计思想,假定采用的数据是具有一定影像重叠的两个干涉像对,所采用的控制点为平面高程控制点,需要解算的是两个干涉像对的基线长度、基线水平角和干涉相位偏置。如图1所示,若采用区域网平差基线估计方法,则在这两个像对中,控制点、连接点都可根据式(4)列出相应的误差方程式。

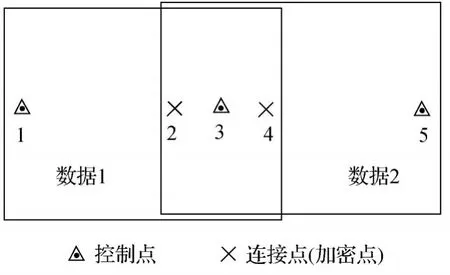
图1 区域网平差基线估计所需控制点Fig.1 Needed GCPs for baseline estimation with block adjustment

以图1中的控制点1为例,所列出的误差方程形式为

而对于图1中的连接点2,由不同像对反演的高程值应相等,因此在平差中考虑了不同数据接边处高程相等的条件,此时连接点2在不同干涉像对中所列出的误差方程分别为

依此类推,对于所有的控制点和连接点,都可列出相应的误差方程式。之后给定未知数的初值,根据误差方程组成法方程式进行各未知数改正量的答解。再根据解算出的未知数改正量对初值进行修正,并对上述计算过程进行迭代,直至满足给定的收敛条件。最后可得到各像对的基线估计和干涉相位偏置解算结果及所有连接点处的高程值加密结果。

此时,需要解算的参数共计2×3=6个,重叠范围内的1个控制点可列1×2=2个误差方程式,其余2个控制点各列1个误差方程式,2个连接点可列4个误差方程式并同时引入2个未知数,所以此时刚好能列2+2+4=8个误差方程式来解算6+2=8个未知数。因而,在整个影像覆盖范围内利用3个分布合理的地面控制点可以进行有效的基线估计。并且当干涉像对数量增多时,利用3个地面控制点仍然可以进行有效的基线估计。

假定需要进行基线估计的干涉像对数为100,且各数据间仅存在两度重叠,控制点均不位于影像重叠范围内,则需要解算的参数数量为n×3=100×3=300,由控制点可列出的误差方程式数量为3×1=3,由连接点列出的误差方程式数量为m×2=2m,由连接点引入的高程未知数数量为m,此时利用3个地面控制点和297个连接点就可以完成100个干涉像对的基线估计和干涉相位偏置解算,有效减少了所需的地面控制点数量。

但是如果采用各像对单独基线估计方法,如图2所示,对于两套干涉数据,则要求每套数据中都至少布设分布合理的3个地面控制点来进行基线估计和干涉相位偏置解算。假定影像重叠区域内存在1个地面控制点,则总共需要至少5个地面控制点。干涉像对数越大,所需的地面控制点数量就越大。当干涉像对数为100时,假定各影像重叠范围内均存在且只存在1个地面控制点,则至少需要n×3-(n-1)×2+(n-1)=201个地面控制点。

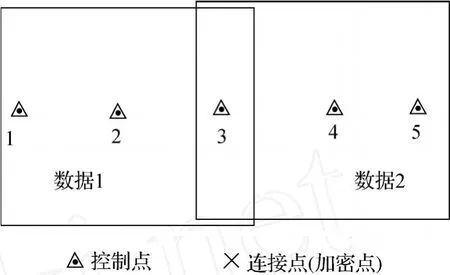
图2 单独基线估计所需地面控制点Fig.2 Needed GCPs for baseline estimation with each data

综上所述,采用区域网平差基线估计方法可以有效减少所需的地面控制点数量。

对于区域网平差基线估计和控制点加密,可采取两种解算方案。

2.1 方案A——整体解法

对于每一个像点(分别对应于控制点和连接点)可以根据式(5)列出一组误差方程式,误差方程式中含有两类未知数Δ1和Δ2。其中,Δ1对应于所有干涉像对的基线参数和干涉相位偏置参数(每个像对有3个参数),Δ2对应于所有连接点的高程值。

相应的法方程式为

对于大区域而言,当涉及的干涉像对数和连接点数很多时,误差方程式的总数十分可观。在解算过程中可先消去一类未知数而只求另一类未知数。考虑到一般选取的连接点数较多,其未知数Δ2的个数远大于干涉参数Δ1的个数,因此消去Δ2以后,可得Δ1的解为

Δ2的解为

本文采用有限元数值模型方法来研究聚合物整体灌装电路板的热应力可靠性。建立含多个电子元器件的电路板有限元模型,如图1所示。

2.2 方案B——两类未知数交替趋近法

首先把连接点处的高程近似值作为已知值,求出每个干涉像对的基线参数和干涉相位偏置,再利用这些参数的新值计算各连接点的高程值,如此反复趋近,直至各干涉像对中各参数改正值和连接点的高程改正值均小于某个限差时,迭代结束。

3 试 验

为了验证本文所提出的考虑干涉相位偏置参数的区域网平差InSAR基线估计方法的正确性和有效性,采用中国科学院电子学研究所机载InSAR系统获取的多套干涉数据进行基线估计试验。在试验区内,包含了平地和山区等典型的地形要素。试验所采用的InSAR系统的部分相关参数如表1所示。

表1 InSAR系统参数Tab.1 Parameters of InSAR

图3～图6分别为试验区的4套InSAR数据强度图。其中,图3和图4为航线0001中相邻两块数据的控制点分布情况;图5和图6为航线1001中相邻两块数据的控制点分布情况。表2为根据SAR强度影像中的明显特征点利用差分GPS到实地测量的高程值。

图3 0001_04控制点分布Fig.3 GCPs’distribution of data 0001_04

图4 0001_03控制点分布Fig.4 GCPs’distribution of data 0001_03

图5 1001_04控制点分布Fig.5 GCPs’distribution of data 1001_04

图6 1001_03控制点分布Fig.6 GCPs’distribution of data 1001_03

表2 高程控制点Tab.2 Height control points

图7～图10为各套干涉数据中选取的连接点分布情况。表3为采用各套数据单独基线估计方法对干涉相位偏置、基线长度和基线水平角进行估计的结果;表4为采用区域网平差基线估计方法对相应各参数进行估计的结果。

图7 0001_04连接点分布Fig.7 Tie points’distribution of data 0001_04

图8 0001_03连接点分布Fig.8 Tie points’distribution of data 0001_03

图9 1001_04连接点分布Fig.9 Tie points’distribution of data 1001_04

图10 1001_03连接点分布Fig.10 Tie points’distribution of data 1001_03

从试验结果可以看出:对于干涉数据1001_ 03,由于覆盖范围内只有两个地面控制点,当采用各像对单独基线估计方法时,由于控制点数量不足,难以进行精确有效地基线估计和干涉相位偏置参数解算;而采用区域网平差基线估计方法,则可根据与其他数据区域的连接点条件,进行精确有效的基线估计和干涉相位偏置参数解算,进而有效地进行高程信息反演,这已经充分验证了区域网平差基线估计方法的优势。

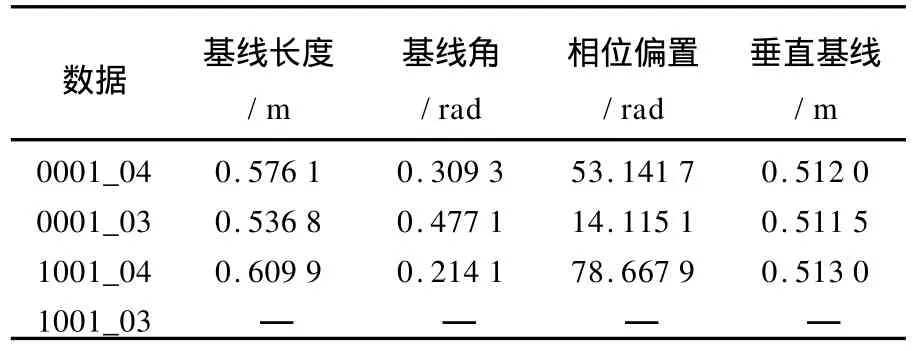
表3 各像对单独基线估计和相位偏置解算结果Tab.3 Estimated parameters with each data

表4 区域网平差基线估计结果Tab.4 Estimated parameters with block adjustment

表5是采用不同基线估计方法获取的基线参数反演的高程值与实测的控制点高程值的差异情况。从表5中可以看出,两种基线估计方法均能高精度地进行高程信息反演,但对于各干涉像对单独基线估计方法要求每套干涉数据中均存在足量分布合理的控制点。

表5 高程差异情况Tab.5 Difference of heights

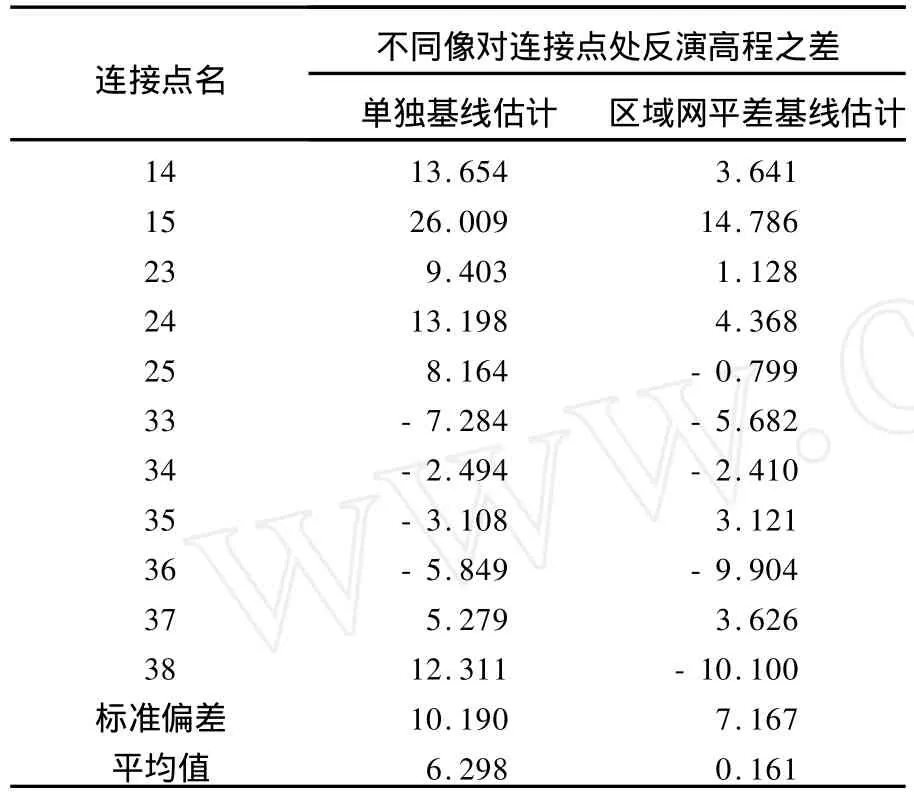
表6 采用不同基线估计方法反演的连接点处高程差异Tab.6 Height difference on tie points with different baseline estimation methods m

考虑到对于数据1001_03,由于控制点数量不足,采用单独基线估计方法无法进行基线估计,表6中仅统计了数据1001_04与数据0001_03、0001_04之间连接点处的高差情况。图11和图12分别表示单独基线估计和区域网平差基线估计后上述连接点处高差分布情况。从表6和图11、图12可以看出,采用区域网平差基线估计方法,反演的连接点处高程之差的均值接近于0。这说明该方法可以有效降低不同数据接边处反演高程的差异。但从得到的标准偏差情况来看,采用区域网平差基线估计方法,虽然可以在一定程度上降低不同数据反演高程之差的标准偏差,但其标准偏差仍较大,这说明得到的高差分布比较离散。分析其原因,主要是所采用的干涉数据在不同数据接边处信噪比较低(通过图4～图6所示的强度图像也能反映这一点,图像两侧色调较暗),干涉相位中噪声影响较大。在后续研究中,将进一步考虑连接点选取对基线估计性能的影响,特别是要避免选取低相干性的点作为控制点和连接点,并且要注意尽量使所选取的连接点分布均匀。

为了说明区域网平差方法对非接边区域的影响,表7给出了采用不同方法进行基线参数估计后反演高程值与实测控制点高程值的差异情况。从表7中可以看出,两种基线估计方法均能高精度地进行高程信息反演。但对于单独基线估计方法要求每套干涉数据中均存在足量分布合理的控制点,对于区域网平差基线估计方法,由于考虑了各套数据之间的误差配赋问题,个别控制点上反演的高程误差略微增大。

图11 单独基线估计后连接点处的高差分布Fig.11 Distribution of heights’difference on tie points with estimated parameters by single data

图12 区域网平差基线估计后连接点处的高差分布Fig.12 Distribution of heights’difference on tie points with estimated parameters by joint adjustment

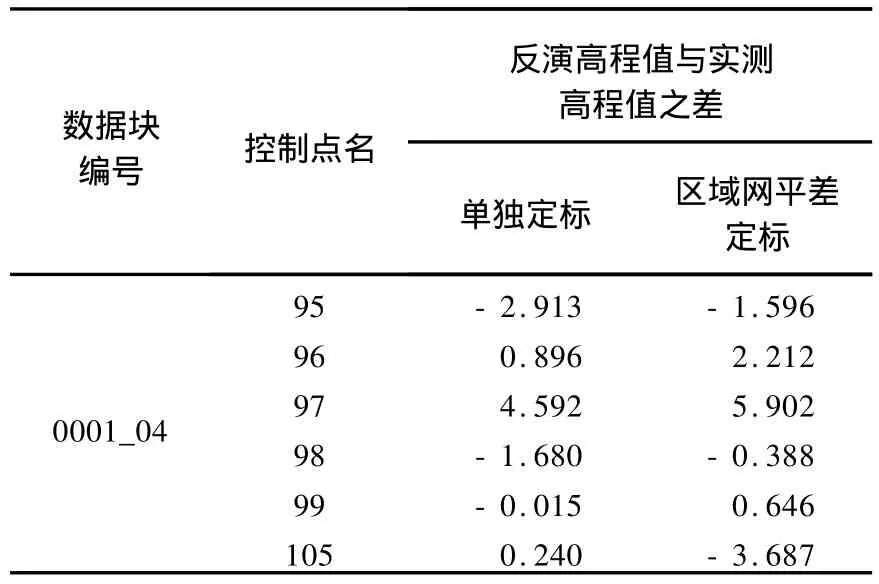
表7 不同方法的反演高程与实测高程之差Tab.7 Difference between derived heights and measured heights with different methods m

续表7 m

4 总 结

基线估计在InSAR系统的实用化测绘应用中具有重要意义。基线估计误差将降低反演高程的精度。为了有效地将InSAR系统用于大面积地形测绘中,本文借鉴光学摄影测量中已成熟运用的区域网平差思想,提出并设计了考虑干涉相位偏置参数解算的InSAR区域网平差基线估计方案,以有效减少对地面控制点数量的需求,并降低不同数据接边处反演高程的差异。

采用中国科学院电子学研究所机载InSAR系统获取的多套干涉数据进行了区域网平差基线估计试验,在少量地面控制的条件下,充分利用重叠区域的连接点条件,对各干涉像对进行了区域网平差基线估计,取得了满意的基线估计结果,明显减小了接边处反演高程的差异,验证了本文所提基线估计方案的正确性和有效性。

本文仅考虑了利用高程控制点和连接点进行区域网平差基线参数估计和干涉相位偏置参数解算。为了进一步提高干涉基线估计的可靠性和精度,在后续研究中,还需考虑将不同类型的控制点(包括平面控制点、高程控制点和平面高程控制点)及连接点引入平差方案并优化平差解算过程。

[1] GRAHAM L C.Synthetic Interferometer Radar for Topographic Mapping[J].Proceedings of the IEEE,1974,62 (6):763-768.

[2] WAN G Chao,ZHAN G Hong,L IU Zhi.Spaceborne Synthetic Aperture Radar Intreferometry[M].Beijing: Science Press,2002.(王超,张红,刘智.星载合成孔径雷达干涉测量[M].北京:科学出版社,2002.)

[3] J IN Guowang.Research on Key Processing Techniques for Accurate DEM Deriving from InSAR[D].Zhengzhou: Information Engineering University,2007. (靳国旺. InSAR获取高精度DEM关键处理技术研究[D].郑州:信息工程大学,2007.)

[4] KOHLHASE A O,FEIGL KL,MASSONNET D.Applying Differential InSAR to Orbital Dynamics:A New Approach for Estimating ERS Trajectories[J].Journal of Geodesy, 2003,77:493-502.

[5] ZHOU Chunxia,E Dongchen,LIAO Mingsheng.Feasibility of InSAR Application to Antarctic Mapping[J].Geomatics and Information Science of Wuhan University,2004,29 (7):619-623.(周春霞,鄂栋臣,廖明生.InSAR用于南极测图的可行性研究[J].武汉大学学报:信息科学版, 2004,29(7):619-623.)

[6] JOUGHIN I R,WINEBRENNER D P,FAHNESTOCK M A.Observation of Ice-sheet Motion in Greenland Using Satellite Radar Interferometry[J].Geophysical Research Letters,1995,22(5):571-574.

[7] DALL J,GRINDER-PEDERSEN J,MADSEN S N.Calibration of a High Resolution Airborne 3D SAR[C]∥Proceedings of 1997 IEEE International Geoscience and Remote Sensing:2.Singapore:IEEE,1997:1018-1021.

[8] MALLORQUI J J,BARA M,BROQUETAS A.Calibration Requirements for Airborne SAR Interferometry[C]∥Proceedings ofSPIE:4173.Barcelona:SPIE,2000: 267-278.

[9] MALLORQUI J J,BARA M,BROQUETAS A.Sensitivity Equations and Calibration Requirements on Airborne Interferometry[C]∥Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium:6.Honolulu: IEEE,2000:2739-2741.

[10] SARABANDI K,BROWN C G,PIERCE L,et al. Calibration of the Shuttle RadarTopography Mission Using Point and Distributed Targets[C]∥Proceedings of IEEE 2000 International Geoscience and Remote Sensing Symposium:6.Honolulu:IEEE,2000:2718-2720.

[11] CHAPIN E,HENSLEY S,MICHEL T R.Calibration of an AcrossTrackInterferometric P-band SAR[C]∥Proceedings of IEEE 2001 International Geoscience and Remote Sensing Symposium:1.Sydney:IEEE,2001: 502-504.

[12] W ANG Yanping,PENG Hailiang,YUN Risheng.Locating Calibrators in Airborne InSAR Calibration[J].Journal of Electronics&Information Technology,2004,26(1):89-94.(王彦平,彭海良,云日升.机载干涉合成孔径雷达定标中的定标器布放[J],电子与信息学报,2004,26(1): 89-94.)

[13] ROTH A,KNOPFLE W,RABUS B,et al.GeMoS:A System for the Geocoding and Mosaicking of Interferometric Digital Elevation Models[C]∥Proceedings of IEEE 1999 International Geoscience and Remote Sensing Symposium: 2.Hamburg:IEEE,1999:1124-1127.

[14] MORA O,PEREZ F,PALA V,et al.Development of a Multiple Adjustment Processor for Generation of DEMs Over Large Areas Using SAR Data[C]∥2003 IEEE International Geoscience and Remote Sensing Symposium: 4.Toulouse:IEEE,2003:2326-2328.

[15] JIN Guowang,ZHANG Wei,XIANG Maosheng,et al. A New Calibration Algorithm of Interferometric Parameters for Dual-antenna Airborne InSAR[J].Acta Geodaetica et Cartographica Sinica,2010,39(1):76-81.(靳国旺,张薇,向茂生,等.一种机载双天线InSAR干涉参数定标新方法[J].测绘学报,2010,39(1):76-81.)

[16] J IN Guowang,XU Qing,ZHU Caiying,et al.Initial Baseline Estimation of InSAR Based on the Phases of Flat Earth[J].Journal of Zhengzhou Institute of Surveying and Mapping,2006,23(4):278-283.(靳国旺,徐青,朱彩英,等.利用平地干涉相位进行InSAR初始基线估计[J].测绘科学技术学报,2006,23(4):278-283.)