数形结合思想在低年级数学教学中的渗透与应用

王 薇

（如皋市安定小学，江苏 如皋 226500）

数形结合思想在低年级数学教学中的渗透与应用

王 薇

（如皋市安定小学，江苏 如皋 226500）

数学是研究现实世界的空间形式和数量关系的科学，数学中的数和形关系非常密切。笔者认为，在低年级数学教学中可有意识渗透“数形结合”思想，利用“形”的直观形象来认识抽象的数和数量关系，是符合儿童认知规律的。“数形结合”，既有助于发展学生的数感，又能促进学生数学思维的发展。

一、以“形”为起点，认识抽象的数

以《认识小数》为例

片断一

师：（出示购物情境图）

水彩笔 美工刀 铅笔 橡皮

12元 3元5角 0.4元 0.8元

师：0.4元是多少钱？

生：4角。

师：对了，4角就等于0.4元。如果用 表示1元，你能画一画、涂一涂，表示出4角吗？

学生独立尝试探究。

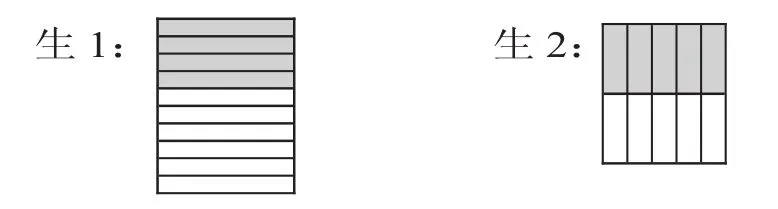
多媒体演示，将一个长方形平均分成10份，涂出其中的4份。 0.4元

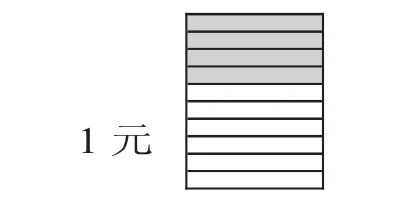
师：看到这个图，你还能想到什么数？生：想到分数，4/10。

师：4角=0.4元=4/10元。

师：橡皮0.8元，你还能用长方形表示1元，表示出0.8元吗？

生：略。

思考：认识小数是苏教版三年级下册的内容，在此之前，学生初步认识了分数。对于“小数”这样一个全新的数，教者从学生已有的“元、角”的十进制的认知切入，尝试在代表1元的长方形上表示出0.4元，利用直观图形，数形结合认识了“0.4元”的实际意义，沟通了分数与小数的联系。

片断二

师：如果继续用长方形表示“1”，平均分成10份，你还能表示出其他的小数吗？

生独立探究完成。

交流整理，师用多媒体显示图形由0.1到1的变化。（略）

师：0.1=1/10，0.2=2/10，0.3=3/10……0.9=9/10，再加1格，10个0.1是多少？

生：10个0.1是1。

思考：这样的设计，堪称“数形结合”的完美演绎。将1元抽象成“1”，表示出其他的小数，由学生的交流反馈整理出从“0.1”到“0.9”再到“1”的发展变化，有效地建立了十进制分数的模型，让学生体会了十进制计数法从整数到分数再到小数的扩展，丰富了数的内涵。因为有了“图”这样一个桥梁，学生对“数”的认识不再是抽象的被动接受的行为，而变成主动的内化沟通的过程。

二、以“形”助数，有效发展数感

用图形来表示数的大小，通过数形结合的方法让学生感悟数的相对大小关系，不仅能培养学生的数感，还有助于低年级学生进行“数学化”的思考。同时，这种方式有效沟通了“数与代数”、“空间与图形”领域的联系。

片断：万以内数的认识

师：老师从五星电器了解到一些电器的价格：海尔电冰箱3600元，联想笔记本电脑的价钱比海尔电冰箱贵得多，小天鹅洗衣机的价钱比海尔电冰箱便宜一些。你能根据线段图估计出笔记本电脑和洗衣机的价钱吗？

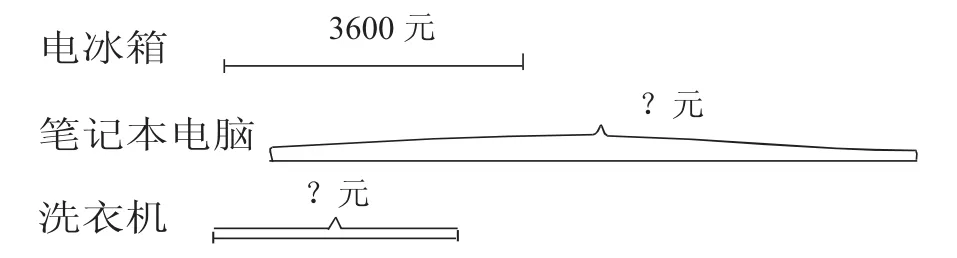
学生根据线段之间的相对大小关系，估算出笔记本电脑大约是7500元，洗衣机大约是2500元。

师：创维平板电视的价钱是4050元，想一想，表示电视机价钱的线段大约该画多长？

这时，有些学生根据电冰箱的价钱来估计，说比表示电冰箱的线段长一些；也有的学生根据表示电脑价钱的线段来估测，说比电脑的线段的一半多一些。

……

思考：这样的设计，因为有了直观图形的支撑，数的相对大小关系也变得形象起来。用线段图表示数量的多少，让学生在这样的数学活动中，感悟相关两个数量之间的关系，从而有效地发展了学生的数感。

三、数形结合，理解数量关系

在低年级解决问题教学中，如果能将一些复杂的数量关系用图形表示出来，无疑可以将复杂的问题简单化，将抽象的数量关系形象化、直观化。对于低年级学生来说，适时地用简单的线段图来帮助分析数量关系，充分利用“数形结合”的思想，对于学生数学思维的发展和解决问题能力的提高都大有益处。

片断：水果店原有600千克水果。第一天卖出125千克，第二天卖出352千克。现在比原来少了多少千克水果？

方法一：（多数学生的解题方法）

现在的重量：600-125=475（千克）

475-352=123（千克）

现在比原来少的重量：600-123=477（千克）

方法二：（少数学生的解题方法）

现在比原来少的重量：125+352=477（千克）

教师请这个同学来说明想法

生：现在比原来少的部分就是第一天和第二天卖出的数量，所以直接用125+352=477（千克）。

教师将数量关系用线段图表示出来后，学生恍然大悟。

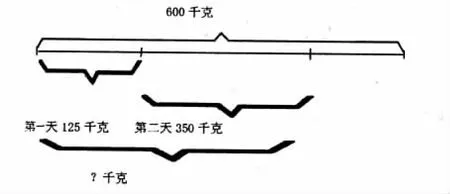
思考：对于二年级学生来说，分析整理数量关系的能力还较弱，解决问题时通常从条件出发进行思考：“水果店原有600千克水果，第一天卖出125千克，第二天卖出352千克。”学生自然而然想先求出现在的水果重量，再用原来的重量减去现在的重量得出减少的部分；或者根据问题进行思考：求现在比原来少多少千克，已知原来的重量，先求出现在的重量。于是大多数学生都是采用第一种解题方法。而教师教学时渗透利用线段图表示稍复杂的数量关系的方法，让学生在直观图形的引导下，发现别有洞天的简单解法，有助于学生数学思维的培养。

总之，在低年级数学教学中，适时地渗透数形结合思想，让学生利用直观形象的图形，将抽象的数量关系具体化，把复杂的解题思路简单化，无形的数形象化，不仅有利于学生顺利、高效地学好数学知识，更有利于学生学习兴趣的培养、数学思维的发展，使教学起到事半功倍之效。

巧妙地渗透、应用数形结合思想，既能为小学数学教学开辟一片广阔的天地，又能为学生的终生学习和可持续发展奠定扎实的基础。

王薇（1978-），女，江苏如皋市人，小学高级教师，本科学历。

李雪虹）