基于贝叶斯网络的平面磨削状态智能监测技术研究

林 峰 焦慧锋 傅建中

1.衢州学院,衢州,324000 2.浙江大学浙江省先进制造技术重点实验室,杭州,310027

基于贝叶斯网络的平面磨削状态智能监测技术研究

林 峰1焦慧锋2傅建中2

1.衢州学院,衢州,324000 2.浙江大学浙江省先进制造技术重点实验室,杭州,310027

为解决平面磨削过程中工件表面粗糙度预测和砂轮钝化监测困难的问题,利用贝叶斯网络建立了平面磨削状态智能监测模型。该模型在获取系统磨削用量和工件材料的基础上,在线提取磨削声发射信号的峭度系数,可以有效预测工件粗糙度和识别砂轮钝化状态,为数控系统调节加工参数提供参考。该模型在平面磨床的磨削监测试验中取得了良好的效果。

平面磨削;贝叶斯网络;声发射技术;粗糙度预测

0 引言

磨削技术在机械制造业中占有极其重要的位置,而平面磨床是光学零件、精密量具部件、机床平面导轨等关键零件精密加工的重要设备。由于磨削往往是零件的终加工工序,所以磨削效果的好坏直接影响到产品的最终质量和性能。但平面磨削普遍存在工件表面粗糙度在线检测困难、砂轮钝化监测困难等直接影响产品质量和生产效率的问题。

国内外学者在磨削加工的状态监测方面进行了大量研究。范兴国[1]采用多元线性回归分析方法进行了大量磨削工艺实验和分析,但由于各影响因素之间存在复杂的关系,给定的模型存在主观性且很难恰当表示复杂的关系,磨削过程又具有很强的随机性,所以预测粗糙度精度并不高;王家忠等[2]将模糊集理论应用于外圆磨削控制中,模糊集理论有逻辑严谨、易于解释等优点,但存在学习能力差、语言变量与隶属度转换难等缺点;T rmal等[3]提出一个基于磨削数据库和知识库的专家系统,但存在容错能力较差等缺陷;史金飞等[4]将粗糙集理论应用到磨削故障诊断中,但是发生多重磨削故障时,其决策表会变得非常庞大。人工神经网络在粗糙度预测和磨削故障诊断中都有应用[5-6],有容错能力强和学习能力强等优点,但是自学习时需要较多的训练数据,在非并行处理系统中的运行速度很慢。

本文采用的贝叶斯网络与传统的模型相比具有以下优点:贝叶斯网络用图形的方法描述变量间的相互关系,可理解性强;贝叶斯网络包含了所有变量之间的因果关系,使得在数据丢失的情况下也能很方便地进行学习。由于磨削过程中产生的声发射信号包含了丰富的磨削加工状态信息,且与磨削状态具有很大的相关性,因此本文将磨削声发射信号中的有效特征提取出来,加入贝叶斯网络,与工件材料、磨削用量等相结合,共同判断砂轮钝化状态和工件粗糙度。

1 平面磨削状态监测系统的构建

1.1 平面磨削状态监测系统的总体结构

本文搭建了平面磨削状态监测系统,它主要由工控机、声发射(AE)采集系统、Surtronic 25型粗糙度仪、工件以及Starline800型数控平面磨床构成,见图1。声发射采集系统的基本构成包括SR150C型AE传感器、PAI型前置放大器、前放供电分离信号器、DAQ-2010高速数据采集卡。工控机主要实现对声发射原始信号进行存储、噪声去除、信号特征提取等功能,并通过磨削状态监测贝叶斯网络实现粗糙度预测和砂轮钝化识别。传感器依靠铁磁吸力固定在工作台上,在传感器和工作台之间涂有黄油,传感器距离磨削区150mm以内。

图1 磨削监测系统结构图

1.2 磨削声发射信号处理

(1)噪声去除。经过声发射采集系统获得的原始信号AE0中含有大量背景噪声,包括低频的机械噪声、环境噪声、摩擦信号及高于2.0MHz的电气噪声。本文设定采样频率为1.0MH z,所以电气噪声不会引入信号中。将空运行过程中采集到的信号与磨削过程中采集到的信号进行FFT变换,对比分析得知背景噪声主要集中在5kH z以下,而磨削信号主要在5～350kH z之间。本文使用MATLAB设计了IIR高通数字滤波器,对磨削噪声进行滤除后得到信号AE1。

(2)生成有效值波形。经过滤除背景噪声的信号AE1包含了复杂的磨削信息,其时域波形中包含了高密度的振荡,因此对其时域有效值(RMS)波形的研究更具有实用价值。本文通过数字方法在工控机内将声发射信号转化为有效值信号,并通过下式进行计算:

式中,T为积分时间常数;N为T内离散数据点的个数;λ为时间变量;Δλt为采样时间间隔。

为了能够有效地提供直观的波形振荡信息用于砂轮接触判断,选定T为1m s,即N=1000,由此得到磨削声发射的RMS信号AE rms。

(3)磨削过程信号提取。进刀过程中的声发射信号只有背景噪声,幅值较小。在砂轮与工件接触后,AE rm s幅值迅速增大,且在磨削过程中保持较大幅值。退刀过程中,AE rm s幅值迅速减小。为了后期更有效地提取磨削信息,在对磨削过程信号处理时,去除了磨削加工开始前及磨削加工结束之后的空行程阶段的信号,只选取磨削加工过程的信号AE g。此外,本文通过监测AE信号RMS值大小来实现砂轮接触判断,设定阈值为0.2V。

(4)信号特征值提取。峭度(kurtosis)是信号的四阶原点矩,将磨削行程声发射信号AEg用离散序列xi来表示,则峭度系数k[7]为

它反映了波形中是否有冲击及曲线的尖峭和平坦程度,本文选取该特征值加入贝叶斯网络中,并通过MATLAB中kurtosis()函数予以实现。

2 基于贝叶斯网络的平面磨削状态智能监测模型的建立

2.1 贝叶斯网络的定义

贝叶斯网络是贝叶斯方法与图模型理论的有机结合,它用一个有向无圈图来描述各随机变量之间的依赖和独立关系。

贝叶斯网络可表示为二元组N=(S,θ),S称

为网络结构,θ称为网络参数。该二元组从定性和定量层面上表示了联合概率分布P(X)。

2.2 磨削状态监测贝叶斯模型构造

贝叶斯网络构建的过程分三个步骤:确定变量集和变量域、确定网络结构和确定网络参数。

2.2.1 确定网络节点及状态

平面磨削状态监测模型的目标是预测工件粗糙度和监测砂轮钝化。磨削产生的声发射信号和工件粗糙度都与磨削用量、工件材料、砂轮状态等相关[9],因此,本文确定变量集为工件材料、砂轮钝化状态、磨削深度、AE rm s波形的峭度系数和工件粗糙度,即确定变量集X={x1,x2,…,x5},网络中的节点分别代表这个变量集中的各个变量。为简化实验验证模型,本文将磨削用量只选取磨削深度进行研究。此外,白刚玉砂轮WA 80G25VCF-2宽度为 50mm,外圆直径为400mm。采用粗糙度仪测量磨削工件的表面粗糙度,由轮廓算术平均偏差Ra表示。工件材料分别为45钢和 Q235钢,长度为 250mm,宽度为40mm。

表1～表3列出了各个节点的状态值离散划分。

表1 各变量节点及其状态

表2 节点x4的离散划分

表3 节点x5的离散划分

2.2.2 确定网络结构

首先要确定变量顺序。本文通过因果关系来建立网络,因果关系的本质就是原因变量在前,结果变量在后。每次磨削过程的磨削深度值都由操作人员在数控系统内设定,工件材料也是提前选定的。工件粗糙度和磨削声发射信号受磨削深度、工件材料、砂轮钝化情况影响,所以选用变量顺序α={x1,x2,…,x5}来构造一个贝叶斯网络结构。

其次,完成有向无圈图。从一个空的有向无圈图N出发,按照变量顺序逐个将变量集X中的变量加入图2中。根据因果关系及各变量之间的条件独立关系,在原因变量到结果变量间连上有向边来表示变量间的因果关系。得到 x4和 x5的父节点集合都为π(x)={x1,x2,x3},而{x1,x2,x3}集合内的变量间相互也无直接明显关系,所以从π(x)的每个变量节点添加一条有向边指向x4和x5,完成有向无圈图N。

2.2.3 确定网络先验参数

确定网络先验参数可以根据大量的经验数据或者通过咨询有经验的专家来进行,但是对于新的磨削机床来说,往往缺乏经验。本文假设网络参数的先验概率分布p(θ)为均匀分布,则本模型中的网络参数为θ={θijk|i=1,2,…,5;j=1,2,…,qi;k=1,2,… ,ri},其中

图2 磨削状态监测有向无圈图N

3 基于贝叶斯网络的平面磨削状态智能监测模型的验证

3.1 基于样本数据的网络参数学习

贝叶斯网络的模型学习包括网络结构学习和参数学习。本文的网络结构S已确定,只需进行参数学习,即通过分析样本数据修正参数的先验分布而获得后验贝叶斯网络参数θ,本文选用计数法进行学习。设αijk和mijk分别代表先验知识和样本数据库D中满足X i=k、π(Xi)=j的样本数目,本文αijk设定都为1。对于p(θ),需假设不同变量的参数相互独立、父节点不同取值时节点的参数相互独立、p(θij.)是狄利克雷分布 D[αij1,αij2,…,αijri],其中 θij.={θijk|k=1,2,…,ri}。

本文设定砂轮线速度为20m/s,工作台纵向进给速度为24m/min。在每次磨削深度和工件材料不变的条件下,砂轮修整完后分别加工8个零件,待砂轮钝化后加工3个零件,实验现场见图3。通过8组实验采集到的各个变量的数据建立了完整数据组D,它由44个样本(D1,D2,…,D44)组成,将D离散化并储存。将样本离散数据代入式(2),计算得到网络的后验参数见表4～表6。

表 4 x1、x3的后验条件概率表 %

表5 x2的后验条件概率表 %

表6 x4、x5的后验条件概率表 %

图3 杭州机床集团实验现场

3.2 模型推理的实验验证

在应用贝叶斯网络推理时,通常将磨削深度和磨削声发射有效值波形的峭度系数作为证据变量,同时,求粗糙度和砂轮钝化的后验条件概率表属于贝叶斯网络的混合推理。本文采用了团树传播法,它是已知的最快的精确推理的算法。团树是一种无向树,其中的每个团代表一个变量集合。假设证据为 x1=1,x3=1,x4=3,求x5和x2的后验条件概率分布表。

3.2.1 构建覆盖平面磨削监测贝叶斯网 N的团树

首先将N端正化。将N中每个节点的不同父节点之间加一条边,然后将所有有向边变为无向边,得到的无向图成为N的端正图Nm,如图4所示。

其次,使用图消元算法构建团树。从端正图Nm出发,按顺序β={x5,x4,x1,x2,x3}在 Nm中进行消元。先消去变量x5,构造一个由x5及图中剩余的所有与其相邻的节点组成的团C1={x1,x2,x3,x5}和用于将该节点与其他节点分隔开来的分隔集S1={x1,x2,x3}。然后消去变量x4,得到 C2={x1,x2,x3,x4}和S2={x1,x2,x3}。因为 C1和C2已包含所有节点,故不再消去剩下的变量x1,x2,x3。将团C2与C1连接,得到一棵覆盖贝叶斯网络N的团树 T(图5)。

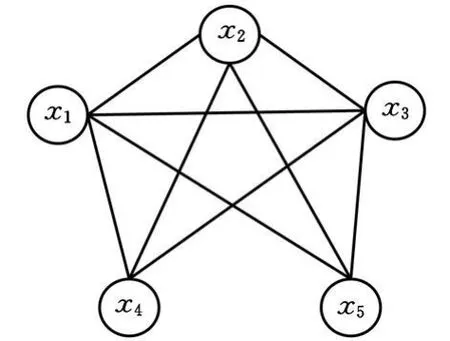
图4 端正图N m

图5 团树T

3.2.2 团树推理算法实现

首先初始化团树。将网络N中每个节点xi的概率函数存储在T中的对应的团内,如图6所示。然后设置证据变量x1=1,x3=1,x4=3,并将C2作为推理的枢纽节点,进行信息传递,如图7所示。

图6 团树T初始化

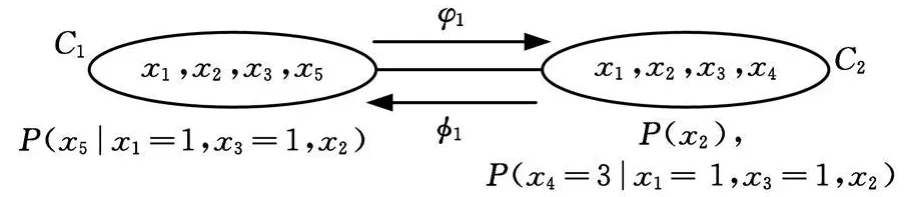
图7 设置证据、信息收集和分发

本文要实现粗糙度预测推理和砂轮钝化识别,网络中对应节点的最大后验概率的状态对实际应用更有意义。在每次磨削深度和工件材料不变的条件下,砂轮修整完后和砂轮钝化后分别加工1个零件,将采集到的样本数据离散化。将证据变量x1,x2,x4输入网络中,根据式(3)和式(4)计算得查询变量x5和x2的最大概率的状态值并与其实测状态值进行对比,见表7。

表7 x2和 x5的实测状态和网络输出状态比较

通过表7中砂轮钝化状态的实际值与网络识别值的对比得平均预测误差为6.3%,粗糙度的实际状态值与预测状态值对比得平均预测误差为7.7%,证明了贝叶斯网络有较好的推理效果。在刚开始学习的阶段,样本量很小,本网络参数的后验概率受先验数据影响较大;经过长时间学习,样本量增大时,后验概率将越来越多地依赖于样本数据,越来越接近真实值。

4 结语

本文研究表明,贝叶斯网络应用于复杂的平面磨削过程分析时,不需要建立确定的数学模型,学习时间和推理时间都很短,且过程具有透明性。通过条件概率分布表来表达磨削参数和磨削粗糙度之间的关系,容易理解。砂轮钝化状态的实际值与预测值对比得平均预测误差为6.3%,粗糙度的实际状态值与预测状态值对比得平均预测误差为7.7%,证明了贝叶斯网络有较好的智能监测效果,表明贝叶斯网络在预测平面磨削的工件表面粗糙度和监测砂轮钝化状态中具有良好的应用前景。

[1] 范兴国.成形磨削表面粗糙度的试验研究[D].长沙:湖南大学,2005.

[2] 王家忠,王龙山,李国发.外圆纵向磨削表面粗糙度的模糊预测与控制[J].吉林大学学报(工学版),2005,35(4):386-390.

[3] T rmal G J,Zhu C B,M idha P S.An Expert System for Grinding Process Optim ization[J].Journal of Materials Processing Technology,1992,33(4):507-517.

[4] 史金飞,钟秉林.基于粗糙集理论的磨削烧伤与砂轮磨钝在线监测[J].中国机械工程,2001,12(10):1151-1154.

[5] 倪其民,林建平,李从心,等.基于人工神经网络和遗传算法的平面铣削加工参数自适应优化[J].组合机床与自动化加工技术,2000(2):5-7.

[6] 巩亚东,吕洋,王宛山,等.基于多传感器融合的磨削砂轮钝化的智能监测[J].东北大学学报(自然科学版),2003,24(3):248-251.

[7] 张利群,朱利民,钟秉林.几个机械状态监测特征量的特性研究[J].振动与冲击,2001,20(1):8,20-21.

[8] 柏航州,王隆太.基于声发射技术的磨削监测系统开发与试验研究[J].现代制造工程,2008(5):121-125.

[9] 张连文,郭海鹏.贝叶斯网引论[M].北京:科学出版社,2006.

Research on IntelligentMonitoring Technique of Machining State for Sur face Grinder Based on Bayesian Network

Lin Feng1Jiao Huifeng2Fu Jianzhong2
1.Quzhou University,Quzhou,Zhejiang,324000 2.The Zhejiang Province Key Lab of Advanced Manufacturing Technology,Zhejiang University,Hangzhou,310027

In order to solve the problem of predicting workpiece quality and identifying blunt level of wheel in surface grinding,a Bayesian netw ork m odel for monitoring grinding states of surface grinder was set up.The model can realize predict workpiece quality and identify b lunt level of wheel by detecting kurtosis of acoustic emission w ith known grinding parameters and w orkpiece m aterial.The results provide reference for NC system to optimize parameters.The technique obtains good effect by experiments on CNC surface grinder.

surface grinder;Bayesian network;acoustic emission;prediction of roughness

TG582

1004—132X(2011)11—1269—05

2011—02—22

国家科技重大专项(2009ZX 04001-131)

(编辑 苏卫国)

林 峰,男,1969年生。衢州学院机械工程学院副教授、高级工程师。主要研究方向为数控技术、精密加工技术。发表论文20余篇。焦慧锋,男,1987年生。浙江大学机械工程学系硕士研究生。傅建中,男,1968年生。浙江大学机械工程学系教授、博士研究生导师。