T-S模糊故障树重要度分析方法

姚成玉 张荧驿 王旭峰 陈东宁

1.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004 2.宁波三星电气股份有限公司,宁波,315191 3.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,066004

T-S模糊故障树重要度分析方法

姚成玉1张荧驿1王旭峰2陈东宁3

1.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004 2.宁波三星电气股份有限公司,宁波,315191 3.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,066004

传统部件重要度分析方法建立在布尔逻辑门的基础上,需要精确已知部件之间的联系,并且不能全面考虑部件所有状态及部件之间的联系对多状态系统可靠性的影响。针对上述问题,首先通过给出传统二态、多态逻辑门的T-S门规则形式,验证了T-S模糊故障树分析方法的可行性,进而将传统二态和多态部件重要度分析方法推广到T-S模糊故障树中,提出了T-S重要度概念及其计算方法,包括T-S结构、概率及关键重要度。然后,与传统部件重要度分析方法进行算例对比与分析,验证方法的可行性。最后,给出了液压系统T-S模糊故障树分析及其重要度计算实例。

故障树;重要度;T-S模型;逻辑门

0 引言

重要度是故障树定量分析的一个重要指标,它不仅能够用于系统的可靠性分析,还可以用于系统的优化设计和指导系统进行维修与诊断。重要度描述了部件发生故障时对顶事件的贡献。传统的故障树重要度主要有结构重要度、概率重要度和关键重要度等。

传统故障树重要度分析基于二态假设,实际系统往往表现为多种故障模式和多种故障程度。文献[1]以多状态串联系统和多状态并联系统为例,利用最小割集和最小路集的概念给出了一般多状态系统的定义。文献[2-3]给出了多态系统元件重要度的一般性定义及其计算方法。

考虑两个元件对系统可靠性的影响,文献[4]提出了联合重要度的概念。文献[5]将两个元件的联合重要度扩展到了多个元件。为了揭示元件所处的状态对状态本身和整个多状态系统故障的影响,文献[6]拓展了传统的概率重要度和关键重要度分析方法,将重要度划分为状态重要度和转移重要度。

上述文献的故障树均以与门、或门等传统逻辑门为基础,使得进行重要度分析时仍需弄清楚故障机理,找到事件间的联系。针对这一问题,文献[7-8]研究了T-S模糊故障树分析方法,将故障树由传统逻辑门拓展到T-S门,降低了建树难度,但是并未给出重要度指标的定义与计算方法,难以全面发挥T-S模糊故障树在可靠性工程中的指导作用与实用价值。

为此,本文在T-S模糊故障树算法基础上,将传统故障树部件重要度分析方法推广到T-S模糊故障树中,提出T-S重要度概念及其计算方法,并与传统故障树方法进行算例对比,结合液压系统实例,验证了该方法的有效性和实用性。

1 T-S模糊故障树分析

用T-S模型取代传统逻辑门来描述事件联系,构造 T-S模糊故障树。图 1所示为一个T-S模糊故障树,其中,y2为顶事件,y1为中间事件,x1、x2、x3为底事件,G1、G2为T-S门。

图1 T-S模糊故障树

1.1 事件描述

在实际系统应用中,部件的状态往往由各种模糊数及语言值来表示,为了便于进行故障树分析,选取图2所示的梯形隶属函数,其中,c为模糊数支撑集的中心,s为支撑半径,f为模糊区。由隶属函数μ(x)描述的模糊数称为模糊数c。

图2 梯形隶属函数

1.2 T-S门算法

1.3 传统逻辑门的T-S门规则形式

1.3.1 二态故障树逻辑门的T-S门规则形式

常见的二态故障树的逻辑门都可以转换为相应的 T-S门规则形式。假设部件 x1、x2为输入,y为输出,且 x1、x2和y有以下两种状态:故障和正常,分别用1和0表示。

在二态与门中,当所有输入事件同时发生时(即x1=1且x2=1),门的输出事件才发生(y=1)。二态与门可用T-S规则表示,见表1。表1中的每一行均代表一条T-S规则,例如第1行的规则是:如果x1为0,x2为0,则y为0的可能性为1,y为1的可能性为0。

表1 二态与门的T-S门规则形式

在二态或门中,至少有一个输入事件发生时(x1=1或x2=1),门的输出事件就发生(y=1)。二态或门可用T-S规则表示,见表2。

表2 二态或门的T-S门规则形式

1.3.2 多态故障树逻辑门的T-S门规则形式

假设部件 x1、x2为输入,y为输出,且 x1、x2和y有以下三种状态:正常、半故障和完全故障,分别用模糊数0、0.5、1来表示。由文献[1]的定义可知,在多状态系统中与门的输出事件的状态为所有输入部件状态中最坏的部件状态;而或门的输出事件的状态为所有输入部件状态中最好的部件状态。三态与门可用T-S规则表示,见表3。例如,第2行所代表的规则是:如果 x1为0,x2为0.5,则y为0的可能性为1,y为0.5的可能性为0,y为1的可能性为0。三态或门可用T-S规则表示,见表4。

表3 三态与门的T-S门规则形式

1.4 故障树算例对比与分析

1.4.1 二态故障树与T-S模糊故障树对比

假设由部件x1、x2和x3组成的T-S模糊故障树如图1所示,令T-S门1为表2所示的二态或门,且 x2、x3和y1分别对应表2中的 x1、x2和y;T-S门2为表1所示的二态与门,且x1、y1和y2分别对应表1中的x1、x2和y;部件x1、x2和x3的故障率(10-6/h)分别为10、2和5。

表4 三态或门的T-S门规则形式

(1)用传统二态故障树分析方法计算y1、y2发生故障的概率分别为

(2)采用T-S模糊故障树分析方法,利用表1、表2和式(1)、式(2)计算 y1、y2发生故障的概率分别为

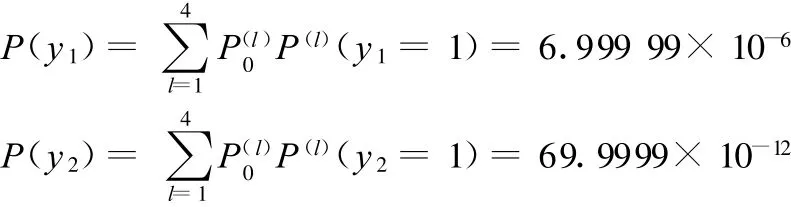
二态故障树分析方法与T-S模糊故障树分析方法的计算结果相同,表明二态故障树分析方法完全可以由T-S模糊故障树分析方法来代替。

1.4.2 多态故障树与T-S模糊故障树对比

假设由部件x1、x2和x3组成的T-S模糊故障树如图1所示,令T-S门1为表4所示的三态或门,且 x2、x3和y1分别对应表4中的 x1、x2和y;T-S门2为表3所示的三态与门,且x1、y1和y2分别对应表3中的x1、x2和y;部件x1、x2和x3的故障程度为1,即部件完全故障的故障率(10-6/h)分别为10、2和5,假设部件发生半故障的故障率与完全故障的故障率相同。

(1)利用传统多态系统故障树分析方法计算y1、y2出现各种故障程度的概率分别为

(2)用T-S模糊故障树分析方法,利用表3、表4和式(1)、式(2)计算y1、y2出现各种故障程度的概率分别为

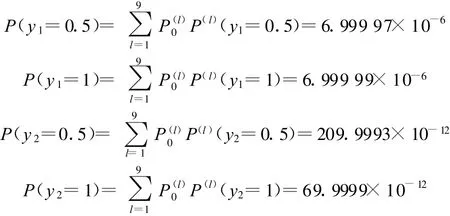
多态故障树分析方法和T-S模糊故障树分析方法的计算结果相同,表明多态故障树分析方法完全可以用T-S模糊故障树分析方法来代替。

通过上述算例对比与分析可知,传统故障树可以看作是T-S模糊故障树中已知部件的模糊可能性时的特例,用T-S门能够描述传统逻辑门,T-S模糊故障树分析方法完全能够胜任传统故障树的计算。

2 T-S模糊故障树重要度分析

2.1 T-S重要度分析步骤

T-S重要度分析步骤如下:①选择顶事件,建立T-S模糊故障树;②将部件和系统各种故障程度分别用模糊数描述,并给出部件处于各种故障程度的模糊可能性;③结合专家经验和历史数据构造T-S门规则表,根据T-S门规则计算部件的T-S结构重要度;④利用T-S模糊故障树分析算法,计算出中间事件和顶事件出现各种故障程度的模糊可能性;⑤定义部件故障程度的T-S概率重要度,进而由顶事件的模糊可能性求得部件故障程度的T-S关键重要度;⑥综合各种故障程度,得到部件的T-S概率重要度以及T-S关键重要度;⑦对T-S重要度进行综合分析,获得部件的重要度序列。

从传统故障树部件重要度出发推广到T-S模糊故障树中,结合T-S门规则给出了T-S重要度定义。令T为故障树顶事件,其故障程度用模糊数Tq(q=1,2,…,kQ)描述。

2.2 T-S结构重要度

定义1 部件xj故障程度为x(ij)j对系统顶事件 T处于水平 Tq的 T-S结构重要度

2.3 T-S概率重要度

(i)

2.4 T-S关键重要度

2.5 重要度算例对比与分析

2.5.1 二态故障树与T-S模糊故障树的重要度算法对比

以1.4.1节的算例为例进行对比分析,以验证T-S重要度定义的可行性。

(1)概率重要度。利用二态系统故障树概率重要度方法计算部件 x1的概率重要度为

二态故障树重要度分析方法与T-S模糊故障树重要度分析方法的计算结果相同,表明T-S模糊故障树重要度分析方法可以用来计算二态故障树部件重要度。

2.5.2 多态故障树与T-S模糊故障树的重要度算法对比[2-3]

以1.4.2节的算例为例进行对比分析,验证T-S重要度定义的可行性。

(1)结构重要度。利用多态系统故障树概率重要度方法计算部件 x1故障程度为0.5对于系统处于水平0.5的结构重要度为

(3)关键重要度。利用多态系统故障树关键重要度方法,由1.4.2节求得的顶事件概率,计算部件x1故障程度为0.5对y2为0.5的关键重要度为

多态故障树重要度分析方法与T-S模糊故障树重要度分析方法的计算结果相同,表明T-S模糊故障树重要度分析方法可以用来计算多态故障树部件重要度。

通过上述算例对比与分析可知,T-S模糊故障树重要度分析方法完全能够胜任传统故障树部件重要度计算。

3 T-S模糊故障树重要度分析实例

3.1 T-S模糊故障树分析

以文献[8]某液压系统为例,建立以动力源系统为顶事件的T-S模糊故障树,如图1所示。其中,顶事件y2代表动力源系统;中间事件y1代表调压块;底事件 x1、x2、x3分别液压泵、插装阀和电磁溢流阀。

假设 x1、x2、x3和 y1、y2的常见故障程度为(0,0.5,1)。其中,0表示无故障,即压力流量正常,系统可完成规定功能;0.5表示半故障状态或轻度故障程度,即压力流量不稳定且达不到规定值,系统不能全部完成规定功能;1表示完全故障或严重故障程度,即压力流量几乎为零,系统不能工作。结合图2所示的梯形隶属函数,参数选为s=0.1,f=0.3。根据文献[8]可得到T-S门规则,见表5和表6。

表5 T-S门 1规则

表6 T-S门 2规则

下面根据上述规则并结合T-S门算法,给出顶事件出现各种故障程度的模糊可能性,计算过程详见文献[8]。

(1)底事件x1、x2、x3的故障率(10-6/h)分别为10、2.4、9.4,这些数据为各部件故障程度为1时的模糊可能性,假设 x1、x2、x3的故障程度为0.5的故障率与为1的故障率相同。由底事件的模糊可能性计算顶事件出现各种故障程度的模糊可能性分别为

3.2 T-S模糊故障树重要度分析

3.2.1 T-S结构重要度

利用式(5)得出部件x1故障程度为0.5对于系统处于水平0.5的T-S结构重要度为

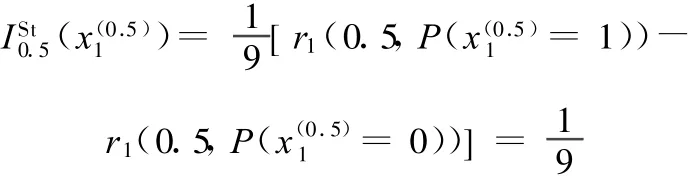
同理可得各部件故障程度为0.5和1的T-S结构重要度见表7。

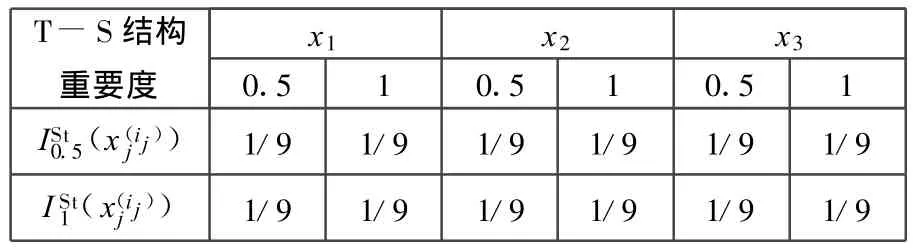
表7 各部件的T-S结构重要度

由表7可知,部件 x1、x2、x3的 T-S结构重要度是相同的,表明它们在故障树逻辑结构中的位置重要程度相同。

3.2.2 T-S概率重要度

利用式(6),得到部件x1故障程度为0.5对y2为0.5的T-S概率重要度为

同理可得各部件故障程度为0.5和1的T-S概率重要度见表8。

表8 各部件故障程度的T-S概率重要度

利用式(7),综合部件x1故障程度为0.5和1的 T-S概率重要度,得到部件 x1对y2为0.5的T-S概率重要度为

同理可得各部件的T-S概率重要度见表9。

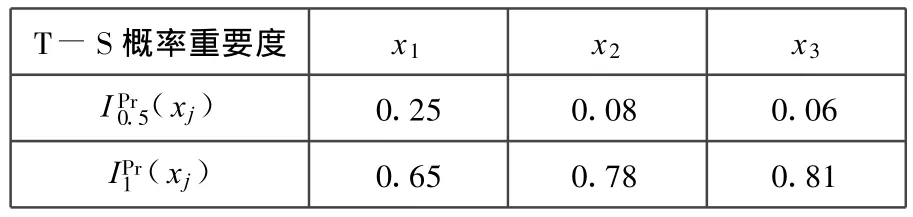
表9 各部件的T-S概率重要度

由表9可知,当系统处于半故障时,x1的T-S概率重要度最大;当系统处于完全故障时,x3的T-S概率重要度最大。

3.2.3 T-S关键重要度

利用式(8),由3.1节求得的顶事件的模糊可能性,得出部件 x1故障程度为0.5对y2为0.5的T-S关键重要度为

同理可得各部件故障程度为0.5和1的T-S关键重要度见表10。

表10 各部件故障程度的T-S关键重要度

利用式(9),综合部件x1故障程度为0.5和1的T-S关键重要度,得到部件 x1对y2为0.5的T-S关键重要度为

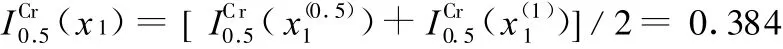
同理可得各部件的 T-S关键重要度见表11。

表11 各部件的T-S关键重要度

由表11可知,当系统处于半故障时,x1的T-S关键重要度最大,则提高液压泵的可靠性对系统可靠性的提升的效果最为明显,同时可按以下次序进行故障排查:x1、x3、x2;当系统处于完全故障时,x3的T-S关键重要度最大,则提高电磁溢流阀的可靠性对系统可靠性的提升的效果最为明显,同时可按以下次序进行故障排查:x3、x1、x2。

上述方法表明,已知的部件故障程度的模糊可能性的T-S重要度,其实质仍是以T-S算法为基础的,T-S结构重要度仅取决于部件状态对应的T-S规则,T-S概率重要度和T-S关键重要度取决于部件故障程度的模糊可能性和对应的T-S规则。

4 结论

T-S重要度分析与传统部件重要度分析方法相比较,具有以下优点:

(1)与传统逻辑门相比,结合专家经验和历史数据的T-S门更接近实际系统情况,能够发挥模糊逻辑推理的优势,从而解决了系统故障机理的不确定性问题,降低了建树的难度。

(2)T-S重要度分析以T-S门为前提,使得重要度分析不再以弄清与、或等传统逻辑关系和最小割集为前提,降低了定量分析的难度。

(3)T-S重要度分析方法更为一般化和精确化,是对传统故障树重要度分析方法的继承与发展,传统故障树重要度分析方法只是T-S模糊故障树重要度分析一个特例。

因此,该方法在机电液复杂系统的可靠性分析及故障诊断中有广泛的应用前景。

[1] Barlow R E,Wu A S.Coherent Systemsw ith Multistates Com ponents[J].Math.of Operation Research,1978,37(3):275-281.

[2] 曾亮,郭欣.多状态单调关联系统可靠性分析[J].方法与应用,1997,70(4):30-33.

[3] 曾亮,郭欣.多状态单调关联系统元件重要度分析[J].系统工程与电子技术,1998(2):72-74.

[4] Wu S M.Joint Importance of Mu ltistate Systems[J].Computers&Industrial Engineering,2005,49(1):63-75.

[5] Gao X L,Cui L R,Li J L.Analysis for Joint Importance o f Components in a Coherent System[J].European Journal of Operational Research,2007,182(1):282-299.

[6] And rew s JD.Birnbaum and Criticality Measures o f Component Contribution to the Failure of Phased M issions[J].Reliability Engineering and System Safety,2008,93(12):1861-1866.

[7] Hua Song,H ong Yuezhang,Chan C W.Fuzzy Fault Tree Analysis Based on T-SModelw ith App lication to INS/GPS Navigation System[J].Soft Computing,2009,13(1):31-40.

[8] 姚成玉,赵静一.基于T-S模型的液压系统模糊故障树分析方法研究[J].中国机械工程,2009,20(16):1913-1917.

Importance AnalysisMethod of Fuzzy Fault Tree Based on T-SModel

Yao Chengyu1Zhang Yingyi1Wang Xufeng2Chen Dongning3

1.Key Lab of Industrial Computer Control Engineering of Hebei Province,Yanshan University,Qinhuangdao,H ebei,066004 2.Ningbo Sanxing Electric Co.,Ltd.,Ningbo,Zhejiang,315191 3.Key Lab of Heavy Machinery Fluid Power Transmission and Control of HebeiProvince,Yanshan University,Qinhuangdao,Hebei,066004

The component importance based on Boolean logic gates,which needed to know exactly the relationships among the components,and could not take into account the influences of all states and components interrelations on the reliability ofm ulti-state system.Therefore,it is p roved thatan analysismethod of fuzzy fault treebased on T-Smodel is feasible by giving the T-S rules of conventionalbinary andmulti-state logic gates.Further,this paper extended the component importance analysism ethod of conventional fault tree to fuzzy fault tree based on T-Smodel.The concept and calculationmethod of T-S importance were presented,including T-S structural,probability and criticality im portance.Finally,an example of fuzzy fau lt tree analysis based on T-Smodel and impo rtance computation of hyd raulic system were given for illustration.

fault tree;im portance;T-Smodel;logic gate

TH 137.7

1004—132X(2011)11—1261—08

2010—08—02

国家自然科学基金资助项目(50905154);高等学校博士学科点专项科研基金资助项目(20091333120005);河北省择优资助博士后科研项目

(编辑 苏卫国)

姚成玉,男,1975年生。燕山大学河北省工业计算机控制工程重点实验室副教授、博士。研究方向为液压系统故障诊断与可靠性。获河北省科技进步二等奖1项。获中国专利3项。出版专著3部,发表论文35篇。张荧驿,女,1986年生。燕山大学电气工程学院系统工程专业硕士研究生。王旭峰,男,1984年生。宁波三星电气股份有限公司助理工程师、硕士。陈东宁,女,1978年生。燕山大学河北省重型机械流体动力传输与控制重点实验室副教授、博士。