基于灰色模型的城市用水量预测

邓丽娟,魏光辉

(1.新疆水利水电科学研究院,新疆 乌鲁木齐 830049;2.新疆 农业大学水利与土木工程学院,新疆乌鲁木齐 830052)

基于灰色模型的城市用水量预测

邓丽娟1,魏光辉2

(1.新疆水利水电科学研究院,新疆 乌鲁木齐 830049;2.新疆 农业大学水利与土木工程学院,新疆乌鲁木齐 830052)

介绍灰色理论建模原理和模型参数辨识方法,并结合实例建立灰色 GM(1,1)预测模型,运用残差检验与后验差检验 2种方法对模型进行精度检验,其模型拟合精度达 99%。用所建立的模型对某市 2010-2013年城市用水量进行外推预测。结果表明,该灰色模型用于城市用水量预测,符合其灰色特性,通用性好,并且所需数据少,计算量适中,预测结果与当地实际情况比较吻合。

GM(1,1)模型;精度检验;城市用水量;水资源利用

0 前言

近年来,随着我国经济的飞速发展,城市规模不断扩张,现有供水系统已经不能满足未来几年的供水需求,必须依照未来城市发展与城市布局进行科学合理的供水系统规划。在充分研究现状资料基础上,对城市未来的人口变化、社会经济发展情况、用水要求和水源保障、现状给水设施、管网布局存在的问题等进行综合分析,合理确定供水规模和相应的供配方式。用水量的预测,既要符合城市发展的需要,又要与水环境和水资源的承载力相适应,以维持水资源平衡及可持续利用[1-2]。

用GM(1,1)模型预测城市用水量,就是利用已发生年份城市用水量数据,建立城市用水量与时间关系函数,通过关联分析等措施提取建模所需要的变量,并在研究离散函数性质的基础上,对离散数据建立微分方程动态模型,进而获得变量时间响应函数[3]。实践证明,灰色建模所需信息较少,精度较高,能较好地反映系统的实际状况[4],可预测未来年份的城市用水量。

本文利用某市 2002～2009年城市用水量资料,建立 GM(1,1)灰色预测模型,对该市用水量的变化进行预测。结果表明,模型精度检验满足要求,可用来对该市的年用水量进行预测。

1 GM(1,1)基本原理

GM(1,1)模型是最常用的一种灰色预测模型,其灰色方程是一个只包含单变量的一阶微分方程。GM(1,1)模型是灰色理论中用于预测的最广泛的模型,建立 GM(1,1)模型只需要一个数列。用微分拟合方程拟合数据的方法来描述事物的发展变化规律,算法简单、速度快捷。最显著的特点是在历史数据较少的情况下,利用 GM(1,1)模型的建立方法预测能达到很好的预测效果。

GM(1,1)模型[5,6]是将随机数经生成后变为有序的生成数据,然后建立微分方程,寻找生成数据的规律,再将运算结果还原的一种方法,其基础是数据的生成。常用的生成方式有累加生成和累减生成。

1.1 GM(1,1)模型的数列预测原理

设某原始序列:式中:α为发展灰数,α的可容区为(-2,2);μ为内生控制灰数。

1.2 为待估参数向量,可利用最小二乘法求解

式(3)、(4)即为 GM(1,1)模型进行灰色预测的基本计算公式。

1.3 灰色预测检验[7]

(1)残差检验

残差检验就是计算相对误差,以残差的大小来判断模型的好坏。

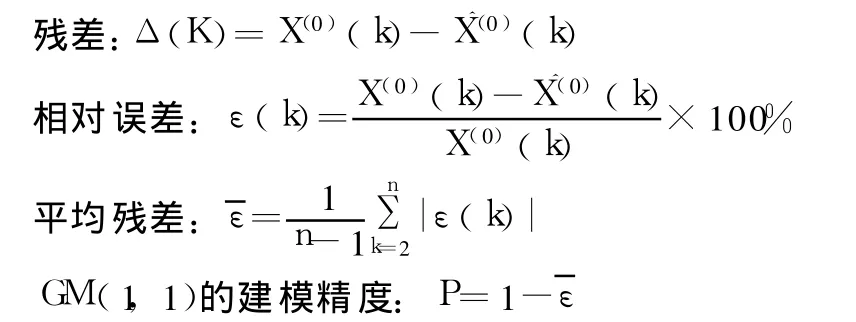
则 ε(k)越小越好,p越大越好,一般要求 ε(k)＜20%,p＞80%;最好是 ε(k) ＜10%,p＞90%。X(0)为原始数列,X^(0)是由式(3)、(4)得到的预测数据列。

(2)后验差检验

式中:S1为原始数列 X(0)的均方差;S2为残差序列{Δ(k)}的均方差;C越小,模型越好。

表1 评价指标等级标准

2 实例应用

2.1 模型计算

运用上述方法,根据某市 2002～2009年用水量数据资料(见表 2),建立 GM(1,1)模型。

表2 某市 2002～2009年用水量

首先对原始数据列 X(0)(t)作准光滑性检验[8]与准指数规律检验:由于 ρ(t)=X(0)(t)/X(1)(t-1),得 ρ(3)=0.521＞0.5,ρ(4)=0.353＜0.5,ρ(5)=0.268＜0.5。当 t≥3时,满足准光滑条件。

检验 X(1)(t)是否具有准指数规律:,σ(1)(t)=X(1)(t-1),得 σ(2)=2.027,σ(3)=1.521,σ(4)=1.353,σ(5)=1.268,当 t≥4时 , σ(1)(5)∈[1,1.5],δ=0.5,准指数规律满足,故可对 X(1)(t)建立 GM(1,1)模型。

依据灰色模型原理建立 GM(1,1)模型,并求得模型参数:a=-0.0335,μ=16.3885,最终得模型计算式为:

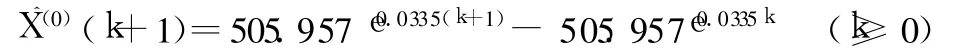
2.2 模型检验

(1)残差检验。经检验,相对误差值为-1%～1%(见表 3)。

表3 模型拟合效果检验

(2)后验差检验。经计算,后验差比值 C=0.0852＜0.35,小误差概率 P=1,模型级别为好。

2.3 用水量预测

经过检验的模型符合精度要求后,可用于外推预测。2010～2013年该市用水量预测结果见表 4。

表4 2010-2013年该市用水量预测

3 结语

针对我国城市中长期用水量序列多属于记录时间较短、历史数据较少的小样本用水量序列的特点,本文提出了灰色系统 GM(1,1)用水量预测方法,建立了 GM(1,1)用水量预测模型,实际验证其精确度可以满足预测的要求。由预测结果看,城市用水量呈逐渐增加趋势,与实际较吻合。随着经济的发展,城市工业化进程的加快以及城市人口逐渐增加,从而导致城市用水量呈增加趋势。

[1]刘百仓,马军,余海艳,等.哈尔滨市水资源开发利用现状及其可持续发展战略研究[J].水利学报,2007(S1):482-484.

[2]赵楠,刘毅,陈吉宁.城市规划实施过程的水资源承载力自适应评估[J].中国环境科学,2008,28(10):944-949.

[3]KUO Hsingchia,WU Lijen.Prediction of heat-affected zone using grey theory[J].Journal of Materials Processing Technology,2002,120:117-119.

[4]TRIVEDIH V,SINGH JK.Application of grey system theory in the development of a runoff prediction model[J].Biosystems Engineering,2005,92(4):521-526.

[5]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990:175-264.

[6]邓聚龙.灰色预测与决策[M].武汉:华中理工大学出版社,1988:59-135.

[7]罗佑新,张龙庭.灰色系统理论及其在机械工程中的应用[M].长沙:国防科技大学出版社,2001:99-103.

[8]东亚斌,段志善.灰色关联度分辨系数的一种新的确定方法[J].西安建筑科技大学学报:自然科学版,2008,40(4):489-492.

Prediction of City W ater Dem and based on GM(1,1)M odel

DENG L i-juan1,WE IGuang-hui2
(1.Institute of Hydrau lic＆Hydropower Research of X in jiang Province,Urumqi 830049,China;2.School of Water Resources＆Civil Engineering,X in jiang Agricu ltural University,Urumqi 830052,China)

Themodeling princip le of grey theory and the recognition method ofmodel parameter were presented.A grey GM(1,1)model was established based on the data of certain city from 2002 to 2009.The precision test of residualerror examination and posterior difference examination showed that the fitting precision reached 99%.The model was applied to the prediction of city waterdemand from 2010 to 2013.The resu lt indicates that this greymodel used in city water demand p rediction conforms to its grey characteristic.Themodelhas the advantages of good versatility,few requirements of data,andmoderate computation quantity,and the result accords with the practical condition.

GM(1,1)model;precision test;city water demand;water resources utilization

TV 213.4

B

1004-1184(2011)01-0100-02

2010-07-01

邓丽娟(1980-),女,新疆乌苏人,工程师,硕士,主要从事水利工程质量检测工作。