嵌入式EPROM数据保持能力评估方法优化

徐海涛，王智勇

（1.无锡华润上华科技有限公司，江苏 无锡 214028；2. 苏州大学电子信息学院微电子系，江苏 苏州 215021）

1 引言

在半导体存储器的产品评估过程中，可靠性评估占有重要的地位。在FAB中开发生产EPROM的晶圆时，当前期的工艺、设备稳定后，EPROM的功能性测试成品率已经达到较高水平后，数据保持能力的评估就摆到了首要的位置。如何有效、经济、快速地评估，对晶圆厂紧跟市场、获取较高利润有直接的影响。由于存储器数据丢失的机理不同，往往在实验的后半程才发现失效，晶圆厂需重新投片、评估，往往半年到一年的时间都没有完成。数据保持能力评估方法的效率高低，往往能够决定这个项目从开发到量产的周期。项目能够尽早开始盈利，是每一个晶圆厂技术研发部门追求的目标。

要使产品满足数据保存“常温下20年/85℃下10年”的业界标准，必须进行老化测试。为了提高评估效率，往往会在不同的高温下进行加速老化并进行验证，150℃/1000h和250℃/24h是业界常用的方法。如何尽快找到产品开发中的问题并采取最终的评估原则是储存器开发阶段的关键工作。其中，确定产品失效中的重要参数——激活能，是一项重要工作。

0.18μm工艺的EPROM从项目引进开始到芯片级（CP）测试良率达到85%后，随后进行数据保持（DR）可靠性测试。测试结果发现在150℃/1000h后数据保持测试始终是通过的，而在250℃/2h后，数据开始有明显的丢失。针对各种失效情况，工艺开发部门做了一些工艺改进，使之能够在250℃下保持到8h~12h时出现失效。如何确定老化温度，提高测试效率（即引入合适的加速因子如24h，确定评估原则）就成为首要的工作。

2 评估测试原理介绍

在可靠性实验中，加速因子的引入对可靠性评估极为重要。产品寿命根据Arrhenius公式可以表示为[1]：

其中k为波尔兹曼常数（8.617×10-5eV/K），T为工作绝对温度，A为一时间常数，Ea为激活能。在同一批次产品中，A、Ea为一常数，与产品失效机制有关，可由实验测定。由公式（1）可得结论一：Ea越大，产品的寿命越长，越不易失效。

为确定某一批产品在某一温度下的寿命（通常指一批产品的平均寿命），进而求得加速评估温度，需确定A和Ea。通常采用以下方法：定义热加速因子TAF，

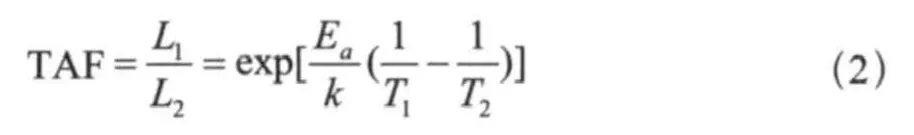
T1、T2为加速温度（如85℃、150℃）。由（2）式得到结论二：激活能越大，温度加速因子TAF也越大；在同样的加速温度下，在同样的时间内没有失效，更能够保证85℃下的寿命，加速试验效果越明显。图1所示为两个不同Ea下的寿命曲线。可见Ea小的电流下降速率快，说明加速老化条件下其失效也快。Ea理论上是一常数（假设所有bit的状态都一样），由不同温度下测试的预估寿命可以得到Ea，由公式（2）知老化温度差值越大，TAF越大。

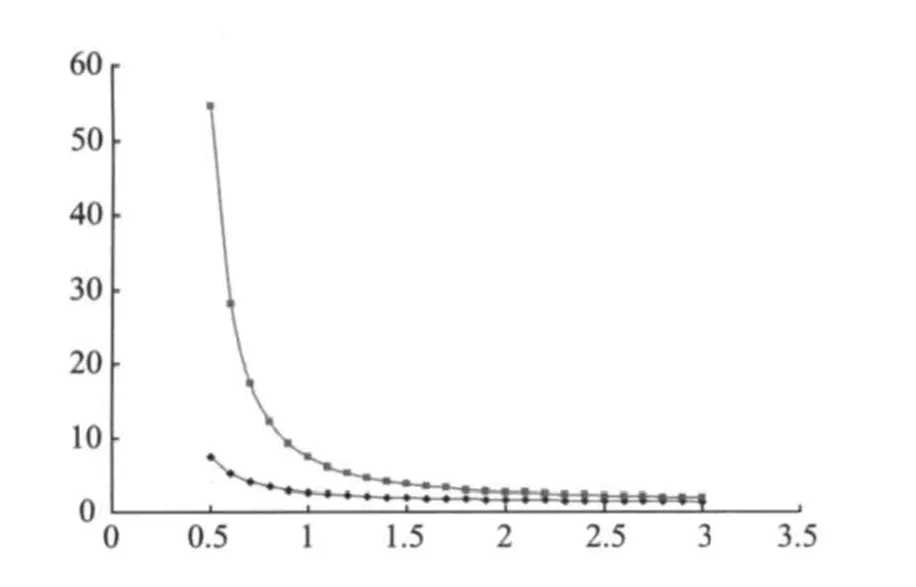
图1 两个不同Ea下的寿命曲线

TAF由要求达到的寿命的比值确定（即理想值），算出来的Ea是理论计算值。将算出来的Ea值代入公式（1），可以得到A。

例如，用150℃/1000h的标准评估在85℃下保存1 0年的激活能，可根据公式（2）首先计算出TAF=365×10×24/1000=87.6，进而得到理论计算值Ea=0.898eV，A=常量。同时，我们看到，老化温度越高，寿命越短。老化温度T2>150℃时，TAF>87.6，产品寿命更短；假如该温度下产品仍然可靠，则在150℃/1000h时产品必然是可靠的，更能满足85℃下10年的要求。

如何确定最终的理论加速老化温度呢？在产品评估的初期150℃/1000h下的标准能够保证产品质量。在批量生产时，鉴于生产控制和成本的考虑，加速老化时间一般设为24h（该老化时间是优化的目标），同样可计算得到TAF=1000/24=41.67，T1=150+273=423，将求得的Ea=0.898eV代入公式（2），可以求得理论加速温度T2=225℃。

实际测量时，TAF由实际测得的寿命决定，算出来的Ea称为实测值。比较理论值和实测值的大小可以判断该产品寿命是否符合要求，实测值大于理想值时，产品是合格的。实际计算加速老化温度时，要以实测的Ea为准。

实际工作中，IC产品可靠性评估通常是以最差的情况来衡量的，所以找出最差的Ea是一个重要的任务。当Ea>0.898eV时，150℃/1000h的评估已经足够了。

已测定的不同电荷漏电机制对应的激活能如表1所示。通常DR失效模式包含多种模式，必须设计实验去确定激活能，从而发现其失效模式。

表1 常见的失效模式和激活能

3 实验方法

由基本器件物理知识知道，存储单元的阈值电压Vt反映了EPROM浮栅的数据保持能力。Vt的变化导致开关电路中源漏电流的变化，它们之间呈线性关系。

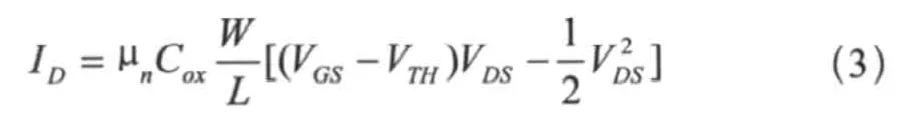
因此，可以通过测量开关电路中源漏电流的变化来检验存储电荷丢失的情况。通过测量来确定激活能，发现失效原因，进而确定评估原则（即使用什么加速因子）。

如何确定产品在某一加速老化温度下的寿命（即失效时间）呢？通常认为，源漏电流与老化时间之间呈负线性关系；低于某一大小的电流，即可判为电路失效，从而可以确定该温度下的寿命。一般可以根据所测的若干个数据点，利用线性规划来求得。Excel软件提供了该功能，可以方便地得到。本实验中，根据开关电路的开关特性，以源漏电流低于6 μ A为失效标准。

4 实验结果

4.1 平均激活能

取EPROM的2000个单元的源漏电流平均值，评估在温度150℃和200℃时随时间变化的趋势，测试数据如表2所示，拟合规划图如图2所示。

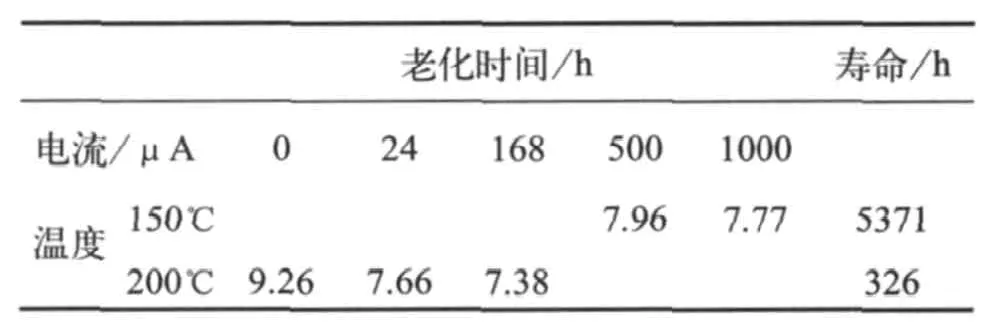
表2 不同老化温度下源漏电流随老化时间的变化

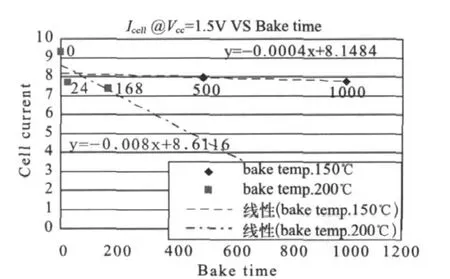
图2 拟合规划图

对所测数据进行线性规划，寿命的规划拟合结果为：5371h（150℃）和326h（200℃）。规划拟合结果也在表2中示出。

由此二数据，再根据公式（2）可计算得到Ea=0.97eV，可见其大于之前的的理论计算，从评估方法来讲，已经能够满足。

同时根据公式（1）对寿命进行指数规划，确定待定的系数A=2×10-8，由此计算得到不同温度下的平均寿命数据为：48 949.4年（25℃）、89.7年（85℃）、25.5年（100℃）。可见该数据满足85℃下10年的要求。

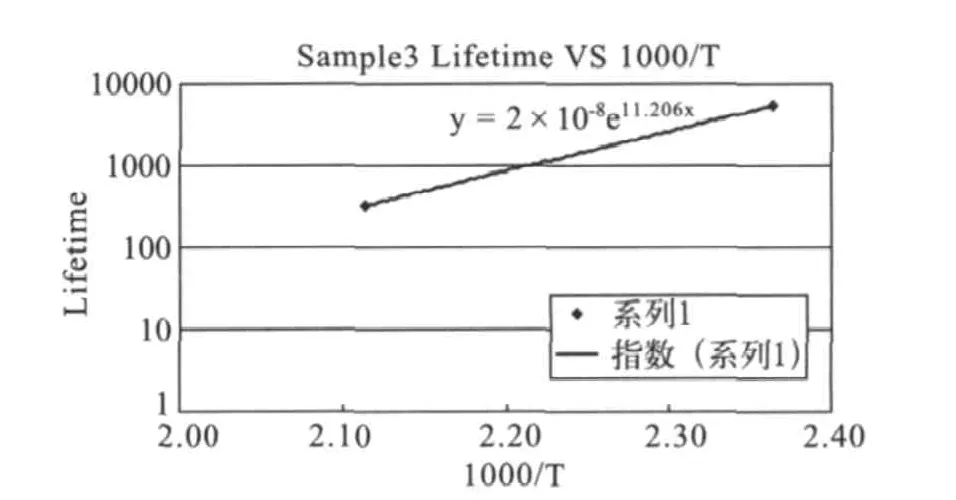
图3 寿命数据图

4.2 最差激活能

评估的第一个阶段，是先用250℃/168h的条件来评估，中间可以采样6h、12h、24h、48h、168h。如果在较短时间内数据丢失严重，可以用紫外线擦除后写入数据，再在150℃下进行评估，可以得到一个较小的Ea。与表1列出的典型值相比较，往往对工艺改进有帮助。

如果150℃/1000h可以通过，而250℃/24h不能通过，同样可以计算Ea，利用Ea反推合适的温度作为评估标准。

选取6组（每组3个存储单元，该3个单元在室温下所测源漏电流尽可能相等，从而表明其可比性）存储单元进行测试，根据失效的判别原则，以大于6 μA输出为0，小于6 μA输出为1，来评判是否有足够的电荷保留在栅级上。测试数据如表3所示。

250℃/12h后的源漏电流均小于6μA，全部判为失效。其中最差的第4个单元，250℃下仅能保存9.21h。这并不意味着不能满足85℃/10年的标准。6个单元的Ea分别为1.05eV、1.08eV、1.03eV、1.06eV、1.06eV、1.08eV，满足85℃/10年的标准。这说明用250℃/24h的评估标准并不适用于该产品。因而选取合适的温度来评估数据保持特性是一个非常重要的工作。

200℃/168h下，采用同样的计算方法得到6个存储单元的Ea分别为0.88eV、0.92eV、0.79eV、0.86eV、0.85eV、0.90eV。选取最差单元的数据Ea=0.79eV，根据公式（1），经拟合计算得到A=9×10-7。由此计算得到不同温度下的寿命数据为：2238.6年（25℃）、13年（85℃）、4.7年（100℃）。这个结果也能满足85℃下保存10年的要求。

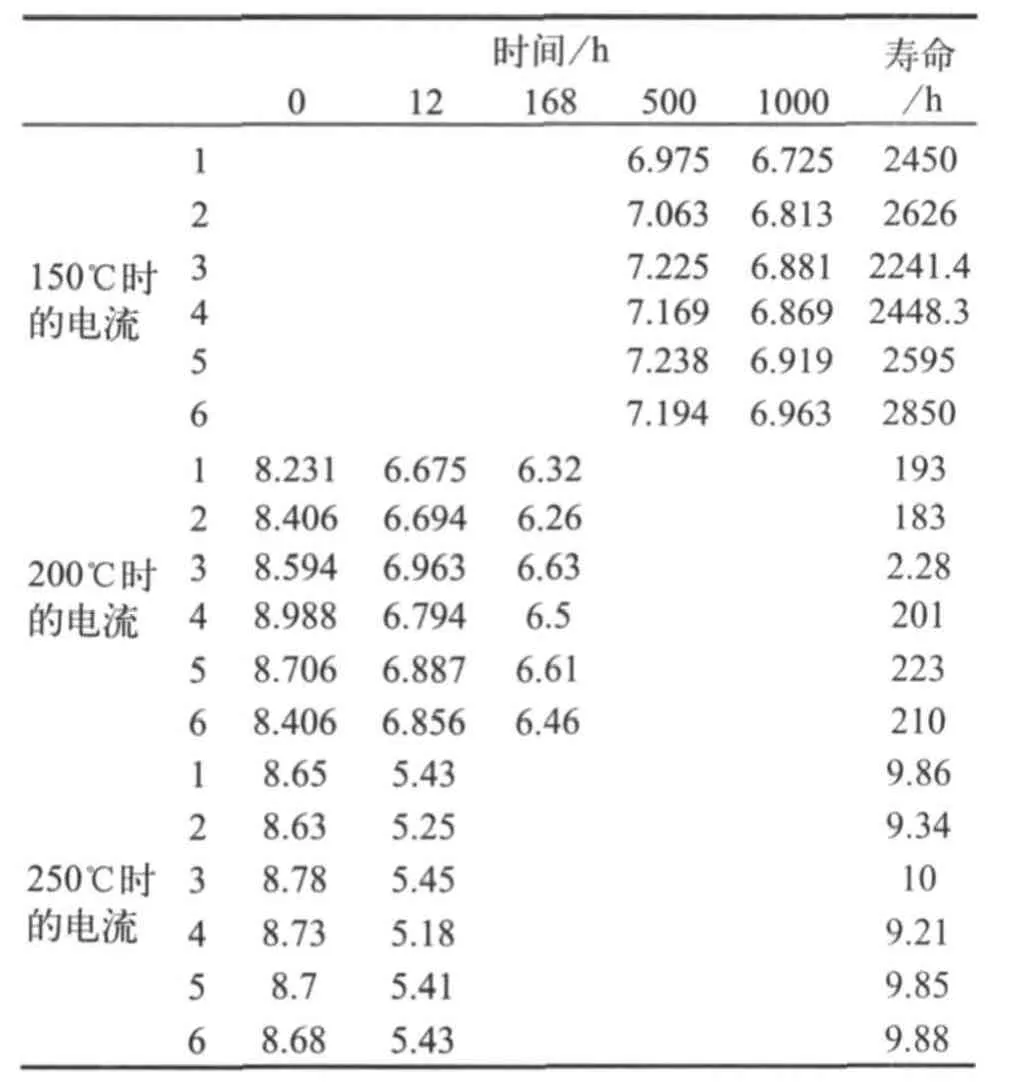
表3 不同老化温度下源漏电流随老化时间的变化二

在做数据保持可靠性评估时，当250℃/24h评估失效时，并不意味着在85℃下不能保持10年。当产品通过150℃/1000h的数据保持评估后，生产工艺往往就固定下来了。个别失效的点可能是生产制造过程中的异常，我们需要计算的是代表正常生产工艺的Ea值，基本上用统计方法来定出典型值（本例用取平均值的方法），便于不同客户通常根据提供的Ea值来评估嵌入式系统中的EPROM在自己电路中的应用情况。但是批量生产前，EPROM的生产工艺稳定后，由Ea的平均值可以推算在什么温度下烘烤24h，可以用来评估85℃/10年的标准。本例为225℃（Ea=0.97eV）。

5 结束语

随着半导体存储器业界越来越关注成本控制和评估中激活能的界定方法、开发周期，合适的只读存储器数据保持能力评估方法愈来愈重要，这里着重探讨经济有效的评估方法，供业界同仁参考。

［1］J.E Brewer, M.Gill. Nonvolatile Memory Technologies with Emphasis on Flash[P]. The Institute of Electrical and Electronics Engineers,INC.2008.

［2］JEDEC Solid State Technology Association. Failure Mechanisms and Models for semiconductor Devices[S].JEDEC PUBLICATION No.122B. 2003.

［3］Ashok K.Sharma. Semiconductor Memories Technology,Testing, and Reliability[M].IEEE Press ,1997:103,270.

［4］马春霞，李冰. 0.5 μm OTP工艺开发与器件特性研究[J].电子与封装，2008，8（7）：34-38.

［5］江英武.Arrhenius方程应用仍须澄清的问题[J]. 含能材料，2009，17（13）.