绝对零度与可溶性物质质量密度的等压膨胀法测量

俞晓明，崔益和

（盐城工学院a．基础教学部b．实验教学部，江苏 盐城224051）

1 引 言

绝对零度是热力学温标的起点，目前公认值为－273．15℃，因其为低温极限，不能用实验的方法直接测量，但可根据气体状态方程用外推的方法进行测量［1－3］．Robert Otani［1］在厨房洗涤槽中利用玻璃管、吸管、橡皮泥、家庭温度计等简易器材进行了实验，实验时吸管竖直放置，水柱难以控制，易滑入玻璃瓶中．Dragia Trifonov Ivanov［2］采用等体升压法和等压膨胀法来测量，实验时文献［2］中图5中气体的压强等于外界大气压，图6中气体的压强大于外界大气压，密闭气体并非严格的等压变化，测得绝对零度值为－273．29℃，偏低．代伟等［3］用贮气球体与压力传感器和温度传感器取代用玻璃管测体积和水银温度计测温度测得绝对零度值为－272．00℃，该实验对器材要求较高，实验步骤相对复杂，实验误差相对较大．

固体物质密度的测量多用流体静力称衡法［4－5］，该方法要求待测物质不溶于水、不吸水或与水不发生化学反应．青一平［6］借助于U型水银压强计等利用玻－马定律测得了大米的密度；饶黄云［7］分别用饱和溶液法、抽气法和玻－马公式法测量了食盐的密度；曹惠贤［8］用玻－马定律测得了食盐的密度，在这些实验中因大米的产地不同，食盐的成分不同，其密度没有公认值，所测结果较难令人信服．

教材［9］将竖直吸管改进为“弯成直角的均匀玻璃管”，张弘权［10］进一步改进为“水平玻璃管两头作钝角弯曲”，同时“在水平玻璃管部分附有刻度尺”．作者借鉴文献［10］中的装置，将水银柱换成水柱，回避取装水银，采用等压膨胀法，既验证了盖吕萨克定律，同时利用该定律测得了绝对零度值和可溶性物质的质量密度．

2 盖吕萨克定律的验证

2．1 实验原理

设一定量气体从状态1经3个等压膨胀分过程依次到达状态2、状态3和状态4，3个分过程中气体体积的变化分别为ΔV1，ΔV2和ΔV3，相应热力学温度的变化为ΔT1，ΔT2和ΔT3，若，则盖吕萨克定律得证．

2．2 实验装置及步骤

如图1所示，A为锥形平底烧瓶，B为橡皮塞，其上插有温度计C、带有密封旋塞的细玻璃管D和两头作钝角弯曲的水平玻璃管E，F为玻璃管后附带的刻度尺，G为水柱，H和I为铁架台，J为铁夹，L为铁圈，K为玻璃杯．

首先，将烧瓶A用铁夹J夹住并固定在铁架台H上，用乳胶滴管向玻璃管E中注入约2 cm的水柱G并将玻璃管、温度计C和细玻璃管D一并插入橡皮塞B，旋开细玻璃管的旋塞使得在用橡皮塞塞紧烧瓶的过程中瓶内气体始终与大气相通．调节固定在铁架台I上玻璃管另一端的高度，使得玻璃管水平．调节固定在铁架台H上铁圈L的高度使平底烧瓶能够浸入装有低温冷水的玻璃杯K中．待烧瓶内气体与低温冷水达到热平衡时旋转细玻璃管的旋塞，使瓶内气体与大气隔断，读时温度计C的读数t1和玻璃管E内水柱在刻度尺F上的读数n1．忽略玻璃管中水柱到烧瓶间空气的体积和细玻璃管中旋塞与烧瓶间的体积，视烧瓶的容积V1为被密封气体的体积．

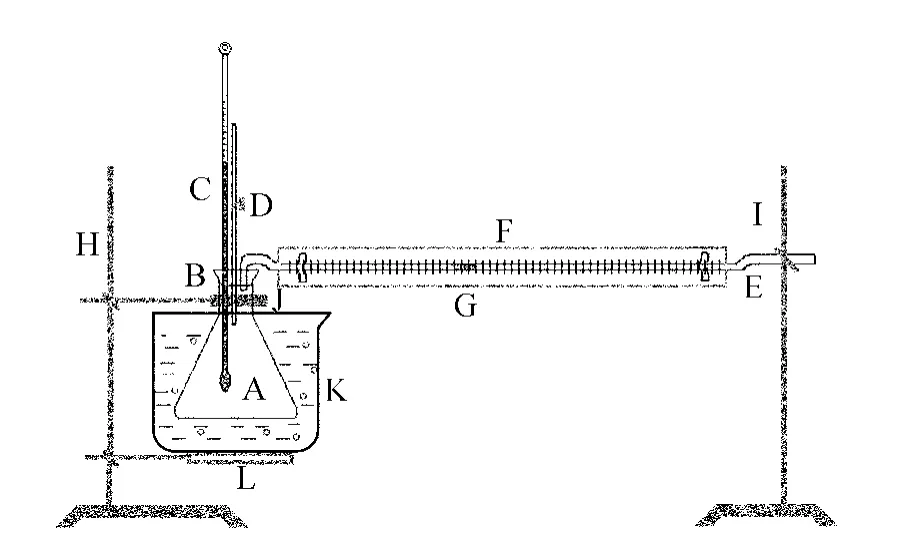
图1 验证盖吕萨克定律实验装置图

其次，移去铁圈和盛水的烧杯，用毛巾擦干平底烧瓶外的水，让烧瓶内被密封的气体在周围空气的加热下等压膨胀，观察玻璃管内水平向右移动的水柱，待瓶内气体与室内气体达到热平衡时读出此时烧瓶内温度计的读数t2及玻璃管内水柱所对应的读数n2．

接着，打开室内空调和取暖器使室内气体温度升高，水柱继续向右移动，平衡时读出此时瓶内温度计的读数t3与水柱所对应的读数n3．

增开暖风机使室温再升高，水柱继续右移，平衡时读出温度计的读数t4和刻度尺读数n4．

最后，旋开细玻璃管上的旋塞，拔掉烧瓶上的橡皮塞，用充水法将平底烧瓶装水至橡皮塞处，倒入量筒内读出水的体积V1，并用游标卡尺测量玻璃管的内直径D，计算玻璃管的横截面积S．

重复以上操作，多次测量求平均值．

2．3 实验数据及结论

表1 盖吕萨克定律验证的实验数据

表2 计算数据 （10－6 m3／K）

3 绝对零度值的测量

3．1 实验原理

一定量的气体在压强不变的情况下，其体积与温度成线性关系（如图2）．设绝对零度值的摄氏温度值为t0．气体在状态1时的摄氏温度为t1、体积为V1，在状态2时的摄氏温度为t2、体积为V2．由盖吕萨克定律得

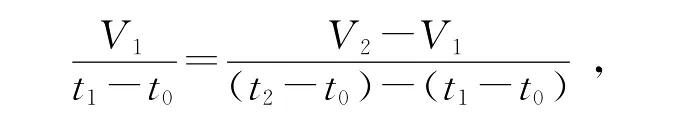
改写上式得绝对零度值

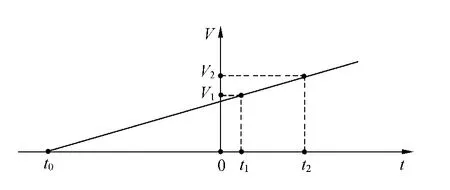
图2 测量绝对零度实验原理图

式（1）中S为玻璃管的横截面积，Δl＝n2－n1为气体从状态1等压变化到状态2的过程中水柱移动的距离．

3．2 实验数据及结论

验证盖吕萨克定律时已测量到了容器的体积V1、玻璃管的横截面积S、气体在状态1和2时的温度t1与t2及此分过程中水柱移动的距离Δl＝n2－n1等数据，利用这些数据计算出绝对零度值如表3所示，得出¯t0＝－272．81℃，δ＝（¯t0－t理）／t理＝0．124%．

表3 绝对零度值的测量数据

4 可溶性物质质量密度的测量

4．1 实验原理

测量溶于水、吸水或与水发生化学反应的不规则固体物质的密度关键在于准确测量体积．通常情况下固体物质与气体的体积膨胀系数相比很小，在一定的实验精度范围内，可认为不随温度变化．

设图1中烧瓶的容积为V1，所装待测物质的体积为Vs，平底烧瓶内气体初始摄氏温度为t1，热力学绝对零度值为t0；保持气体压强不变，使烧瓶内气体的温度升高至t2，相应体积的变化ΔV＝SΔn，S为玻璃管的横截面积，Δn为水柱移动的距离．根据盖吕萨克定律有

整理得

式（2）中V1，t1，t2，S 和 Δn 都可通过实验测量出或计算出．

式（2）从原理上讲是可行的．考虑到实验所用玻璃管较细且长，气体进入玻璃管后散热快，容易冷却到室温．因此，根据气体状态方程将式（2）修正为

得

根据式（3）计算出待测固体的体积Vs，然后由质量密度公式计算出待测物质的密度．

4．2 实验过程

首先，取适量待测物质大米测其质量m后装入烧瓶，用铁夹夹住烧瓶并固定在铁架台上，用滴管向玻璃管中注入水柱，旋转细玻璃管的旋塞使得在用橡皮塞塞紧烧瓶的过程中瓶内气体始终与大气相通，片刻后旋转细玻璃管的旋塞，使瓶内气体与大气隔断，读出此时温度计的读数t1和玻璃管内水柱对应的读数n1．

接着，调节铁架台上铁圈的高度，使烧瓶浸入玻璃杯．向玻璃杯中加入适量的热水，用水浴法对平底烧瓶加热，待瓶内气体与热水达到热平衡时，记录此时气体的温度t2和水柱处刻度尺的读数n2．

4．3 实验数据及分析

应用图1所示的实验装置对大米密度进行了测量，所测数据及计算结果如下：mr＝144．49 g，t1＝8．45 ℃，n1＝10．48 cm，t2＝39．90 ℃，n2＝103．67 cm，S＝2．12×10－5m2，V1＝2．77×10－4m3，V3＝8．01×10－5m3，ρr＝1．80×103／（kg·m－3）．

实验中由于大米的产地不同，密度没有公认值，可信度不高，用同样的方法测量标准锌粒的密度，数据如下：mZn＝501．41 g，t1＝11．13℃，n1＝9．25 cm，t2＝32．36 ℃，n2＝76．46 cm，S＝2．12×10－5m2，V1＝2．77×10－4m3，V3＝7．17×10－5m3，ρZn＝6．99×103／（kg·m－3）

实验测出锌粒密度ρZn测＝6．99×103kg／m3，标准值ρZn标＝7．12×103kg／m3，误差δ＝1．83%，表明测量可溶性物质的质量密度采用等压膨胀法测量是可行的，所测结果是可信的．

5 误差分析及注意事项

实验误差产生的主要原因有：1）水存在表面张力，引起气体体积增量ΔV＝SΔn小于理论值，加之在不同温度时水的表面张力不同［11］，而验证盖吕萨克定律和测量绝对零度的实验中，气体末态的温度要高于初态的温度．2）为防止水银中毒，实验时将水银柱换成了水柱，而密闭气体在不同温度下因水蒸气所导致的压强不同［12］，这一点文中尚未考虑．

实验时应注意合理选择玻璃管．若玻璃管内径过小，则因气体膨胀水柱移动的距离将很大，实验所需玻璃管过长，不利于实验；若玻璃管内径过大，则不能形成水柱．

6 结束语

通过巧设实验装置，采用等压膨胀法既验证了盖吕萨克定律，同时提供了除玻－马定律以外的方法测量了绝对零度值和可溶性物质的质量密度．该方法对实验器材的要求不高，既可作为绝对零度和固体物质质量密度测量实验的有力补充，也可作为学生课外探究的实验选题．

［1］ Otani R，Siegel P．在厨房洗涤槽中测定绝对零度［J］．郑青岳，译．物理教师，1992（6）：23－24．

［2］ Ivanov D T．Experimental determination of absolute zero temperature［J］．Physics Teacher，2003，41（3）：172－175．

［3］ 代伟，兰小刚，谢春茂．用压力传感器和温度传感器测量绝对零度［J］．大学物理，2008，27（9）：30－32．

［4］ 刘映栋．大学物理实验教程［M］．2版 ．南京：东南大学出版社，1998：41．

［5］ 何捷，陈继康．基础物理实验［M］．南京：南京师范大学出版社，2003：27．

［6］ 青一平．可溶性固体微粒密度的测量［J］．物理实验，1992，14（6）：278－279．

［7］ 饶黄云．测量可溶性物质的密度［J］．物理实验，2001，21（12）：32－34．

［8］ 曹惠贤．可溶性物质质量密度的测量［J］．大学物理，2004，23（1）：37－38．

［9］ 人民教育出版社物理室．初级中学课本（第二册）［M］．北京：人民教育出版社，1983：33．

［10］ 张弘权．盖吕萨克定律演示实验的改进［J］．技术物理教学，2002，10（6）：26．

［11］ 朱海，邓若鹏，陈元杰．设计控温装置研究液体表面张力系数与温度的关系［J］．物理实验，2009，29（9）：40－42．

［12］ Ivanov D T．Experimental verification of Boyle’s law and the ideal gas law ［J］．Physics Education，2007，42（2）：193－197．