一种基于磁敏感加权成像技术的三维脑静脉提取方法
【作 者】锁时,窦菲菲,王成,许建荣,黄昕,钱黎俊,许修
1 上海交通大学医学院生物医学工程系,上海,200025
2 上海交通大学医学院附属仁济医院,上海,200127
3 上海交通大学物理系,上海,200240
磁敏感加权成像(SWI)是一种较新的磁共振成像技术。它利用成像中产生的相位图来增强具有不同磁敏感系数的组织之间的对比度[1],在显示大脑微小静脉的效果上优于其它成像技术。在高强磁场下获得的SWI图像中,可以看到更加完整的大脑静脉结构[2]。如能进一步分割提取出静脉血管,则可为诊断颅内静脉病变和微出血灶等提供新的手段,也可为测量脑静脉血氧饱和度等新技术的开发建立良好的基础[3]。
尽管SWI能够显示出0.25 mm粗细的静脉血管[4],但要从SWI图像中分割出静脉却并不容易。其原因主要有两方面:其一,因为静脉分支十分细小,且一些细小侧枝的信号十分微弱,因此在分割提取的过程中极易造成缺失;其二,虽然在经过处理后的SWI图像中静脉表现为低信号,与周围组织有较大的对比度[5],但是由于其它顺磁性组织的干扰,尤其是铁质沉积部位,如基底红核区域及豆状核、纹状核等组成的基底活动中心区域,也呈现出跟静脉相似的低信号,极易与静脉信号混淆,使得静脉的分割变得十分困难。为解决上述问题,从而准确地分割出SWI中的静脉信息,本研究在综合考虑了血管的形状特征及灰度特征后,提出了一种基于血管增强扩散滤波的自适应阈值生长法。
1 原理和方法
由于SWI图像中静脉形态复杂,管径细小,且存在其它顺磁性组织的干扰,因此采用任何单一的分割方法,都无法达到令人满意的效果。本研究在自适应阈值分割的基础上,加入了血管增强扩散滤波器(VED),既考虑了静脉的管状结构特征,又考虑了静脉在SWI图像中的灰度特征,以期获得更好的分割效果。
1.1 血管增强扩散滤波
血管增强扩散滤波器(VED),由Manniesing[6]提出,是建立在Frangi[7]的血管增强函数基础上的。因为Hessian矩阵[8-9]的特征值与物体的几何结构有关,为增强血管的管状结构,可用Hessian矩阵特征值构造的函数作为VED法的扩散系数,以此控制扩散的方向朝着血管的管状方向进行,而其它方向则受到抑制。Hessian矩阵对于血管的检测有十分重要的意义,图像的最小特征值对应的特征向量代表着最小曲率的方向,即表示了血管的方向,而最大特征值对应的特征向量的方向表示了与血管方向垂直的方向。假设Hessian矩阵的三个特征值大小排列为:│λ1│≤│λ2│≤│λ3│,为区别出血管和其他结构,Frangi利用Hessian矩阵的特征值构造了一个血管增强函数,此函数由三个变量组成。
第一个变量可区别管状结构与板状结构,用长宽比进行定义:

第二个变量可区别管状结构与圆块状结构,可用球形度进行定义:
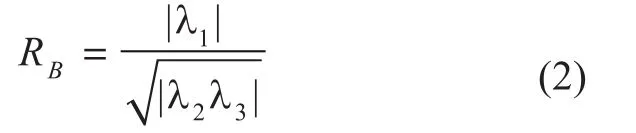
第三个变量可区别出图像噪声信号,定义为:
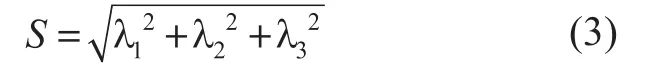
对于不同形状,三个变量所代表值的关系可用表1清楚表示出来。
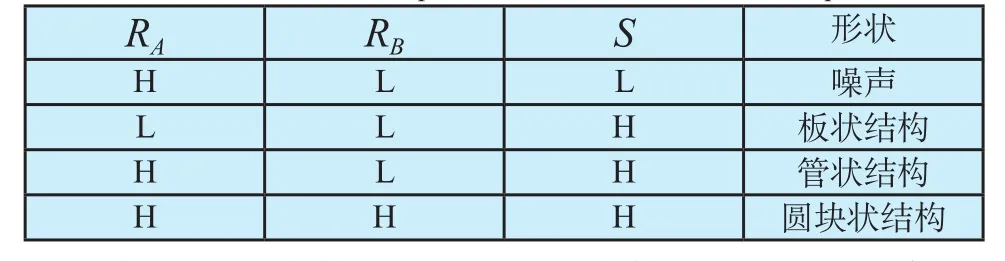
表1 三个变量与形状的关系表Tab.1 The relationship between three variables and shape
表中 L代表较小的值,H代表较大的值。可见每个变量可区别出一种非管状结构,综合考虑这三个变量,血管增强函数可定义为:
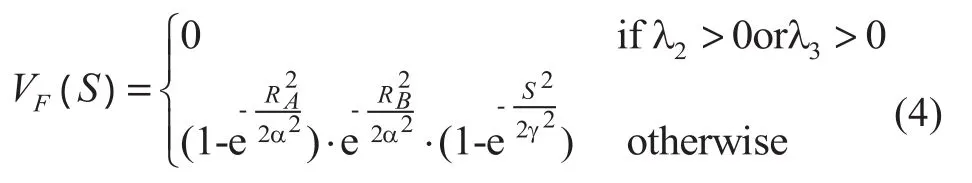
式中:α、β和γ可调节血管增强函数对RA,RB,S这三个变量的敏感性。在本研究中,α和β都取0.5,γ 取决于SWI图像的平均灰度值,一般取为平均灰度值的10%[10]。对于图像中的每一点,VF(S)为一个从0到1的值,定义了此点属于血管结构的可能性。
针对血管具有不同管径的问题,采用多尺度的方法对血管增强函数的响应进行计算,即对图像计算不同尺度下的血管增强函数响应,比较各尺度下的响应值,选取其中最大的响应作为最终的响应值:
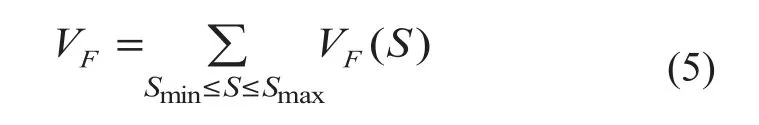
在此血管增强函数的基础上,即可构建扩散系数D。为满足仅在血管方向上进行扩散,而垂直于血管方向的扩散被抑制的要求,对D作出如下定义:

式中:Q是Hessian矩阵的特征向量矩阵;∧'为以血管增强函数定义的对角矩阵,其对角线上的值为:
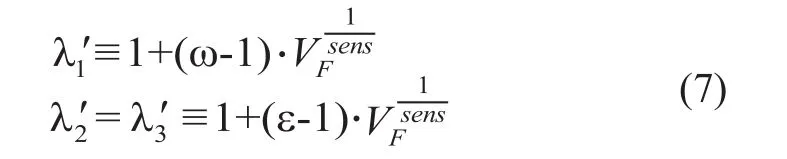
式中:参数ω一般设为较大的值,表示各向异性扩散滤波器的强度,ε则一般设为很小的值,但必须大于0,以满足扩散系数的D正定性的要求。sens可调节扩散函数的敏感性。在本研究中,ω=25,ε =0.01,sens=5.0[6]。
对于非血管结构,VF接近于0,则三个特征值相等,扩散强度很高,且为各向同性;而对于血管结构,VF接近于1,在最小曲率的方向(λ'1)(沿着血管方向)扩散强度达到最大值(为ω),在与血管的垂直方向(λ'2,λ'3)扩散强度极小(为ε),从而抑制了此方向上的扩散。最后通过扩散公式(8)对图像进行循环计算;

为了观察VED法对团块状的顺磁性伪影的抑制效果,从原始图像中截取出一块含有团块状伪影的感兴趣区域(如图1a所示),其VED滤波后的结果以及应用基于血管增强扩散滤波的自适应阈值生长法提取的结果分别如图1b、1c所示:由白色箭头指向的区域可见,对于非血管结构,经过VED滤波后,其信号被抑制,表现为灰度值居中的信号,且分割时将其滤除了;由红色箭头指向的区域可见,对于血管结构,经过滤波后,其信号被增强,表现为灰度较低的信号,且分割时将其提取了出来。
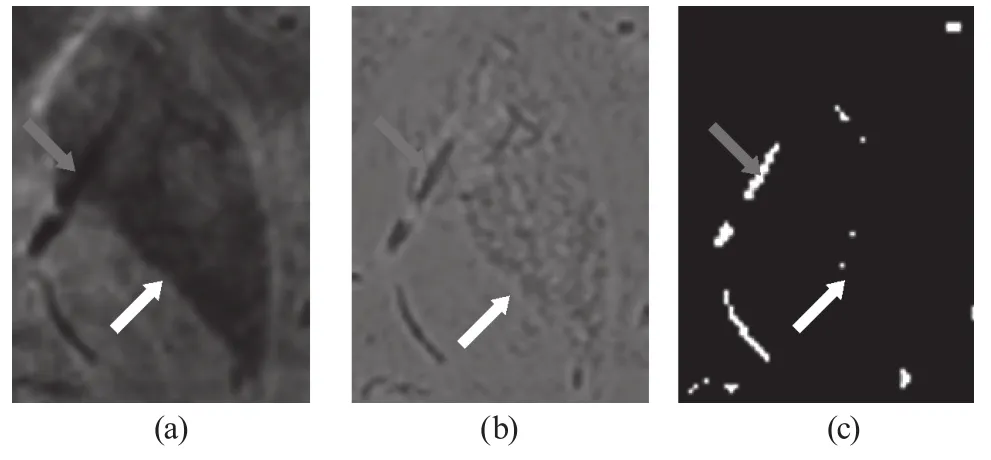
图1 (a) 含有团块状伪影的感兴趣区域(b) VED滤波后的结果图;(c) 分割后的结果图Fig.1 (a)The region containing nucleus areas;(b) The VED result;(c)The segmentation result
1.2 改进的自适应阈值生长法
自适应区域生长算法[11]是从总体灰度一致性较差的背景中分割提取感兴趣对象所常用的方法之一。然而由于微小静脉的信号较弱,容易被误认为是噪声,而在铁质或钙质沉积的部位,因其顺磁性特征而拥有与静脉相似的灰度特征,因此如果仅考虑图像的灰度信息,极易丢失重要的小静脉信息或错误地分割出铁质沉积区域。由上述可知,VED算法可沿血管方向对血管结构进行增强,并可对非管状结构进行抑制,因此可将VED的输出结果作为血管可能性的参数,将此参数与灰度信息结合,以综合考虑灰度信息和形状结构信息。具体算法如下所述。
1.2.1 种子点的自动选取
种子点的设置主要是基于像素灰度及形态要素。考虑到经过BER-SWI法[12]预处理后的图像中,静脉的信号被映射到了极高的强度,因此可采用Ostu法自动获得一阈值。将阈值以上的点作为种子点备选,然后对此备选集中的点进行判断,求出其同一层面中周围同类点的个数,即获得此种子点所属区域的面积。若此面积低于所设定的值Tseed,则将其作为种子点,这是因为单条静脉在单层中所占的面积一般较小。在本算法中,Tseed设为20。对Tseed的设置要求并不是很高,在15-30范围内皆可。因为生长方式是三维的,只要一段静脉的其中某一层面的点纳入种子点范围,则此段静脉即可被生长出来。
1.2 2 生长准则
本研究采用的生长准则,综合了对象的全局灰度信息、局部灰度信息以及管状结构信息,具有良好的分割性能。
为避免自适应阈值的结果陷入一个局部极值,本研究采用已生长出的静脉区域的平均灰度值作为其全局特征要素Tg:

局部特征Tl的设定参考了简单自适应阈值分割法的准则,选用邻域中包含的所有像素的灰度均值 μ和标准方差σ来确定。考虑到预处理后的图像中静脉显示为较高的信号,因此取拟合的高斯分布的前半部分作为其局部特征要素:

式中,f 是用户提供的系数因子,用以控制像素值的取值范围。
为达到对管状结构敏感的目的,应使属于管状结构的点容易通过阈值的筛选,即对应管状结构的阈值应尽可能小;而对于非管状结构,其对应的阈值应尽可能大。而是否为管状结构,可通过血管增强滤波后的结果It加以判定。在It中,血管管状结构被增强,其滤波结果为较暗的像素;非管状结构则被抑制,其滤波结果为较亮的像素(如图1c所示)。因此,可对It进行灰度映射操作,以使管状结构对应的像素点的灰度值映射到1以下的值,以减小其阈值,增加获取的可能性;而使非管状结构对应的像素点的灰度值映射到1以上的值,以增大其阈值,抑制获取的可能性。其公式可描述为:

式中,It为VED滤波后的结果图,其像素灰度范围是0~255,Th为选定的阈值,以区分管状结构和非管状结构,Th以上的值被映射到1以上的范围,Th以下的值被映射到1以下的范围;E为对比度调整参数,须为大于1的值。在本研究中,Th和E的经验值分别为125和3。综合以上三个特征,自适应的阈值公式为:
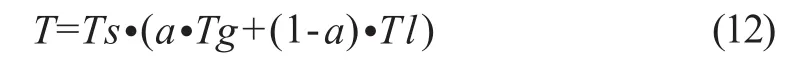
式中,a为调节全局阈值和局部阈值比例的参数,在本研究中的经验值为0.1。
2 实验结果及讨论
本研究的图像数据为Philips Acheiva 3.0T磁共振成像系统同时采集的幅值图与相位图(分辨率为336像素×336像素×180像素),并用BER-SWI方法处理后的SWI图像数据,在Visual C++ 6.0开发环境下采用本研究的方法对整个三维数据进行了静脉数据提取。图2显示了1例受试者的全脑静脉的三维绘制结果。本算法在原有算法的基础上有两方面的改进:① 原来无法获得的细小静脉被检测出来了,从而使得提取出来的微小静脉的数量大大增加;② 由图中箭头所指向的区域可见,团块状的基底活动区域已被滤除。
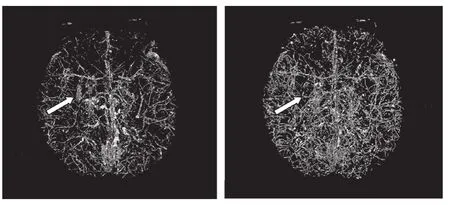
图2 (a)原始自适应分割结果的正视图(b)改进后的分割结果的正视图Fig.2 (a) The front view of the segmented; (b) The front view of the segmented result of the original method result of the improved segmented
我们对5例受试者的SWI图像进行了测试,分别应用普通自适应阈值生长法及本研究提出的基于血管增强扩散滤波的自适应阈值生长法进行分割,然后比较两种分割方法的结果。假定普通自适应阈值生长法分割出的静脉像素数为Norg,应用本研究提出的算法分割出的静脉像素数为Nimp,则提取出的静脉的增加率可用指标IR=((Nimp-Norg)/Norg)×100%来衡量,统计结果为,IR=(18.41±0.47)%。我们从这5例受试者的SWI图像中截取出既有不同粗细静脉又有团块状伪影的典型区域(图3a方框中所示区域的前后二十层数据)进行测试,将这一区域的静脉图像由医生作逐点修正后,保存作为对比的标准图像Istd(如3b所示),将分割的结果作比较,可说明以下两个问题。
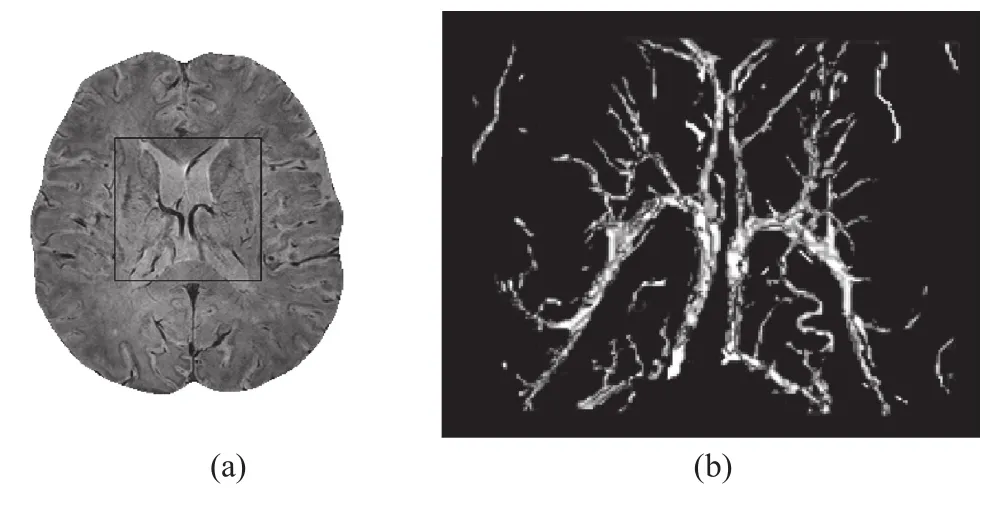
图3 (a) 典型的感兴趣区域 ;(b) 标准静脉图的三维显示Fig.3(a) The typical region of interest;(b) The 3D rendering of the standard vein image
(1) 新方法增加的静脉是否是真实的静脉 设在该区域中用普通自适应阈值法得到的静脉二值图为Iorg(以静脉像素为“1”,背景像素为“0”),新方法得到的静脉二值图为Iimp,将Iimp与Iorg重叠相减,得到二值图I0(其中Iimp-Iorg>0的像素为“1”,其余像素为“0”),为Iimp中增加的静脉。这由两部分组成:一部分与Istd重合,可认为是原方法没有提取的静脉,记为Io1;另一部分是在Istd之外的部分,可认为是噪声引起的伪静脉,记为Io2,I0=Io1+Io2。分别统计Io2、Istd中像素为“1”的个数,对应记为No2、Nstd,可用AR=100%×No2/Nstd来表达新算法增加的静脉部分的误差率。
(2) 团块状伪影的滤除率:将Iorg与Istd重叠相减,得到二值图IForg(其中Iorg-Istd>0的像素为“1”,其余像素为“0”),为Iorg中的伪静脉。同理,将Iimp与Istd重叠相减,同样可得到二值图IFimp,为Iimp中的伪静脉。将Iorg和Istd作“与”运算,得到二值图ITorg,为Iorg中的真实静脉。同样方法,将Iorg和ITorg作“与”运算,得到二值图IRES,为Iimp相对于Iorg保留的真实静脉。分别统计IForg、IFimp、ITorg和IRES中像素为“1”的个数,对应记为NForg、NFimp、NTorg和NRES,可用下述指标衡量新算法对团块状伪影的滤除性能。新、旧方法的相对误差之比,REM=(1-NFimp/NForg)×100%,其百分比越大,说明滤除的伪影越多。那么滤除的是否是伪影,则可通过测算经滤波措施后Iimp和Iorg中属于真实静脉的符合率(或称为保留率)RES来表达,RES=(NRES/NTorg)×100%。REM越大,说明新算法对团块状伪影的滤除率越高;同时RES越大,说明新算法相对于原算法,其滤除的部分确实是各种伪影,而对真实静脉的影响越小。
对5例数据的实验结果按上述方法作定量分析,其统计结果见表2所示。结果表明,本文提出的算法在原有基础上提高了微小静脉的检出率达18.41%,其误差率仅为1.57%。而且,因为REM=(86.11±0.48)%和RES=(98.41±0.39)%,都是比较大的百分比,可以认为新算法有较好的滤除效果,且滤除的部分基本都属于伪影,而非真实静脉。图1所示也证实了这点。
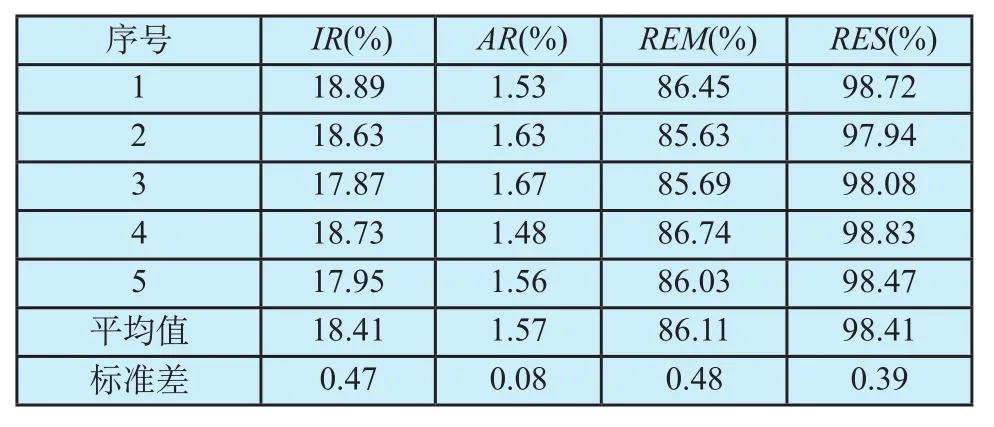
表2 定量分析结果Tab.2 The quantitative analysis results
3 结论与展望
本研究在对原始磁敏感加权图像进行一系列的预处理后,采用了血管增强扩散滤波器和改进的自适应阈值分割相结合的方法,综合考虑了脑部静脉的局部灰度特征、全局灰度特征以及管状信息,提出了一种基于血管增强扩散滤波的自适应阈值生长法,从而增强了静脉的连续性,提高了细微静脉的检出率,解决了团块状的顺磁性伪影干扰,准确无创地分割出了SWI图像中的静脉信息,并用专家勾勒的结果验证了算法的有效性。为进一步开展基于脑静脉的临床生理和病理方面的研究,以及脑静脉血氧饱和浓度无创测量的研究奠定了基础。
[1] E. Mark Haacke, Yingbiao Xu, Yu-Chung N. Cheng, et al.Susceptibility Weighted Imaging(SWI)[J]. Magnetic Resonance in Medicine, 2004, 52(3): 612-618.
[2] Yimin Shen, Zhifeng Kou, Christian W. Kreipke, et al. In vivo measurement of tissue damage, oxygen saturation changes and blood flow changes after experimental raumatic brain injury in rats using susceptibility weighted imaging[J]. Magnetic Resonance Imaging, 2007, 25:219-227.
[3] Yu-Kun Tsui, Fong Y. Tsai, Anton N. Hasso. Susceptibilityweighted imaging for differential diagnosis of cerebral vascular pathology: A pictorial review[J]. Journal of the Neurological Sciences, 2009, 287: 7-16.
[4] 王彩云, 张强, 薛敏. 磁化率加权成像:一种对颅内血管疾病敏感的MRI技术[J]. 国外医学(临床放射学分册), 2007, 30(2):135-140.
[5] 钱黎俊, 路青, 许建荣. 磁敏感加权成像的后处理算法与临床应用[J].计算机工程, 2008, 34(13): 1-3.
[6] Mannieshing R., Viergever M.A., and Niessen W. J. Vessel enhancing diffusion: A scale space representation of vessel structures[J]. Medical Image Analysis, 2006, 10:815-825.
[7] Frangi A. F, Niessen W. J, Vincken K. L, etal. Multiscale vessel enhancement filtering[J]. Medical Image Computing and Computer-Assisted Intervention. 1998, (1):130-137.
[8] C. Lorenz, et al. Multi-scale line segmentation with automatic estimation of width, contrast and tangential direction in 2D and 3D medical images. In J. Troccaz, E.Grimson, and R. Mösges,eds., Proc. CVRMed-MRCAS'97, LNCS, 1997, 233-242.
[9] Y. Sato, et al. 3D multi-scale line filter for segmentation and visualization of curvilinear structures in medical images. In J. Troccaz, E.Grimson, and R. Mösges, eds., Proc. CVRMed-MRCAS'97, LNCS, 1997, 213-222.
[10] Rashindra Manniesing and Wiro Niessen. Multiscale vessel enhancing diffusion in CT angiography noise filtering[J].Computer Science, 2005, (3565): 138-149.
[11] Pole R. and Toennies K. D. A new approach for model-based adaptive region growing in medical image analysis[C]. 9th Int.Conf. on Computer Analysis and Patterns, 2001: 238-246.
[12] 窦菲菲, 许建荣, 王成, 等.磁敏感加权脑静脉成像中的磁场不均匀性伪影滤除技术[J]. 中国生物医学工程学报, 2010, 29(1): 60-65.

