凸多边形闭区域的参数方程及应用

李 盛,阮建苗

(1.浙江省衢州第一中学,浙江衢州324000;2.浙江外国语学院理工学院,浙江杭州310012)

1 引言及主要结果

在传统的解析几何中,通常是将曲线作为点的轨迹进行研究,而平面闭区域则一般是讨论边界的光滑性问题,没有专题讨论过平面闭区域的方程问题.本文将凸多边形闭区域看作点的轨迹,给出它的一种简洁的参数方程,并简要叙述其应用.

凸多边形是指这样一类多边形,在多边形内任选两个点,将这两个点用线段连接后,此线段上所有的点都在多边形内.我们称,由凸多边形及其内部围成的平面闭区域为凸多边形闭区域.在凸多边形外部(不含凸多边形)的平面区域称为凸多边形外区域.

文献[1]利用三角形面积相等的方法,证明了点P在凸n边形A1A2…An闭区域上的充要条件是

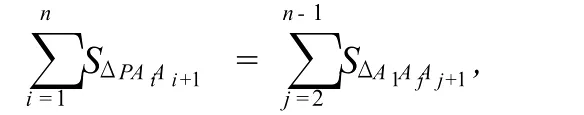
其中An+1=A1.求出了凸多边形闭区域的一种形式上较为复杂的用行列式表示的参数方程下面我们给出一种简洁的参数方程.

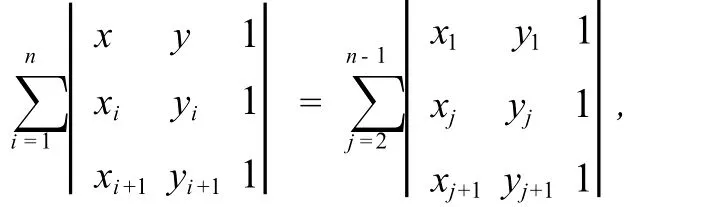
定理1 设凸n边形A1A2…An闭区域DA1…An的顶点坐标为Ai=Ai(xi,yi)(i=1,2,…,n),则DA1…An的参数方程为

注:当n=3时,凸3边形A1A2A3闭区域即为三角形△A1A2A3,此时(1.1)式的表示唯一,但当n≥4时,(1.1)式的表示不唯一,详细的理由可参见定理必要性的证明.

2 定理的证明

下述引理是显然的:

引理1 设A1(x1,y1),A2(x2,y2),则M(x,y)表示线段A1A2上任意一点的充分必要条件是存在λ∈[0,1],使即线段A1A2可看作动点M(x,y)的轨迹.

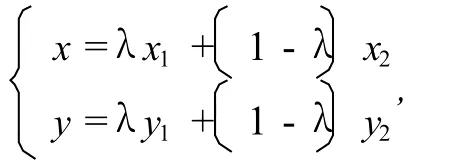
2.1 充分性

我们用数学归纳法来证明定理的充分性.

证明 当n=3时,如图1所示,若α3=1,则可得α1=α2=0,

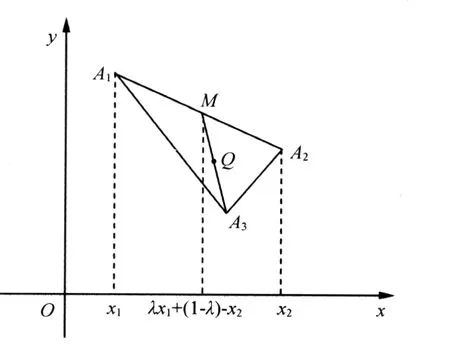
图1 凸3边形闭区域

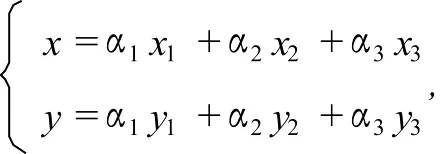
对应的点是A3(x3,y3).

若α3≠1,令α1=λ(1-α3),则故

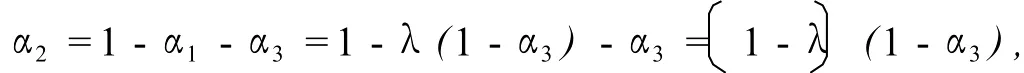
此时

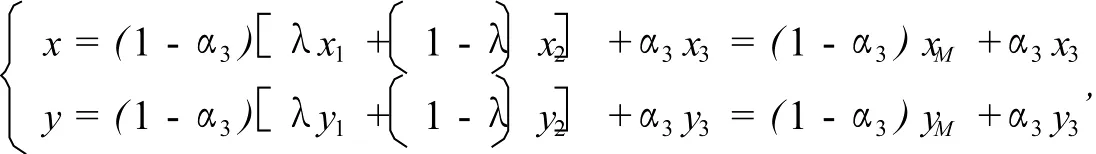
可见点Q(x,y)在线段MA3上,也在△A1A2A3中.

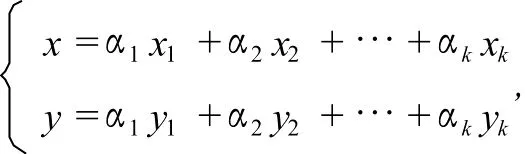
其中确定的点(x,y)都在凸k边形A1A2…Ak闭区域中.

当n=k+1时,需要研究由参数方程组

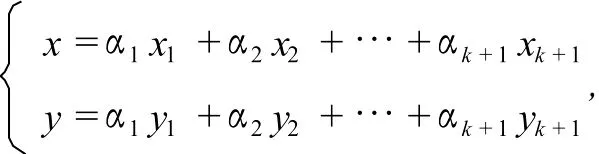
若αk+1=0,参数方程组变为

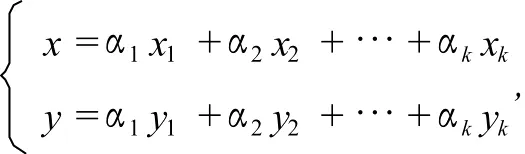
若αk+1=1,参数方程组变为

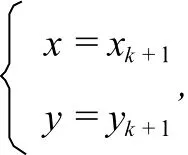
(x,y)表示顶点Ak+1.

当0＜αk+1＜1时,参数方程组可变为

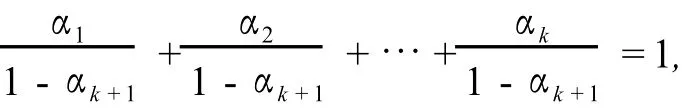
所以根据假设,由参数方程组

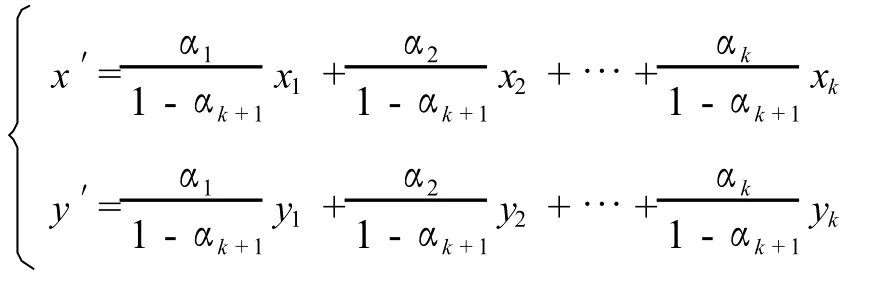
确定的点Q′(x′,y′)在凸k边形A1A2…Ak闭区域中.根据引理1,由参数方程组(2.1)确定的点在线段Q′Ak+1上,所以也在凸边形A1A2…Ak+1闭区域中.证毕.

2.2 必要性

证明 如果Q(x,y)是表示凸n边形A1A2…An闭区域DA1…An中的任意一点,若Q(x,y)位于DA1…An的某一条边上时,则由引理1知结论显然.若Q(x,y)位于DA1…An的内部时,不妨连接A1Q,其延长线必与某一边AiAi+1相交,记交点为M(xM,yM).又由引理1知,存在常数λ∈(0,1)与β∈[0,1]使得

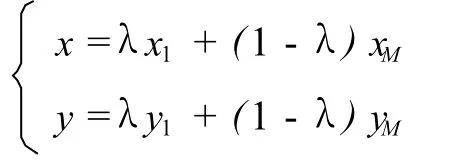
与

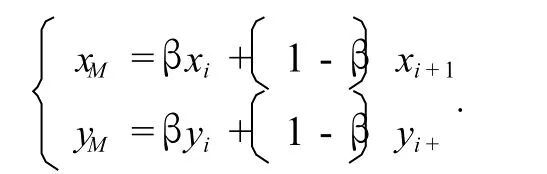
于是

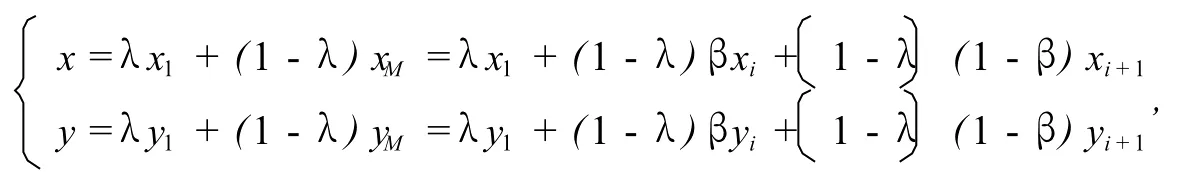
其余xi,yi前的系数取0,即为所求.证毕.

3 应 用

3.1 与凸多边形闭区域有关的面积和最小值问题

解1 令α3=1-α1-α2,则α3≥0,α1+α2+α3=1,已知α1,α2≥0,根据定理1,由参数方程

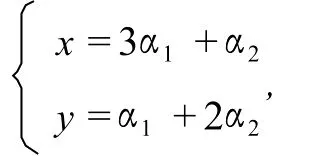
其中α1,α2≥0,且α1+α2≤1围成图形是三角形△OAB,其中O(0,0),A(3,1),B(1,2),容易求得面

解2 由参数方程可反解,得

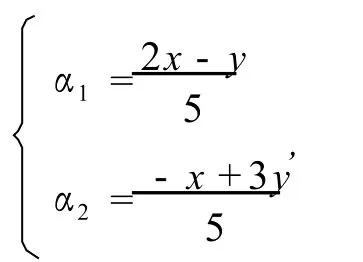
代入约束条件α1,α2≥0,且α1+α2≤1,得

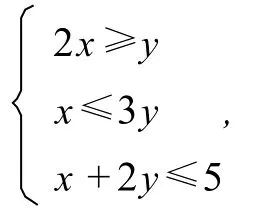
注:比较方法1与2,可知方法1的解法更简洁.

解 根据定理1,知由题设所给的参数方程围成的图形是凸4边形A1A2A3A4闭区DA1…A4,如图2所示,其中A1(1,2),A2到原点O(0,0)的距离,最小值就是原点到直线A1A2:y=-3x+5的距离,

3.2 Jensen不等式的几何解释

Jensen不等式作为数学中的一个著名不等式,在性质和应用方面都被广泛的研究过[2-7].

例3 Jensen不等式是指:设f(x)是定义在区间I上的连续函数,对于xi∈I(i=1,2,…,n),若

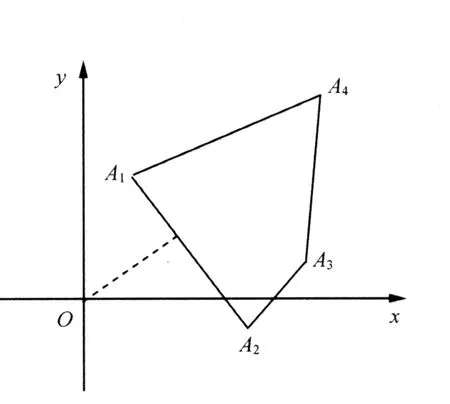
图2 凸4边形闭区域

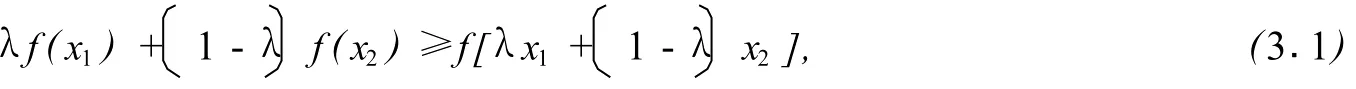
其中λ∈[0,1].则对αi≥

我们熟知(3.1)式的几何意义比较清晰,但(3.2)式又有怎样的几何意义呢?据我们所知,没有人对此问题作出过回答.下面给出答案.

当n=2时,如图3,若λ∈[0,1],则M点坐标

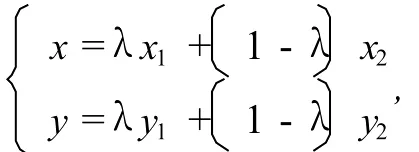
这时我们看到,λf(x1)示P点纵坐标,由(3.1)式知,此时函数为凸函数,由图3,(3.1)式表明

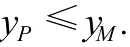
一般地,记Ai(xi,yi),x1＜x2＜…＜xn,1≤i≤n,n≥3.则对任意的=1,记

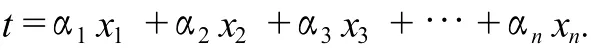
由定理1知,

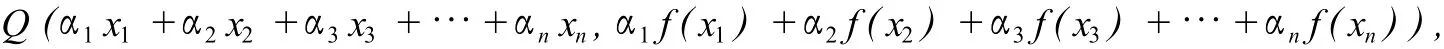
表示DA1…An中的一个点,即图4中的点Q,而f(α1x1+α2x2+…+αnxn)即P点纵坐标,由图4知Jensen不等式的几何意义即

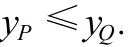
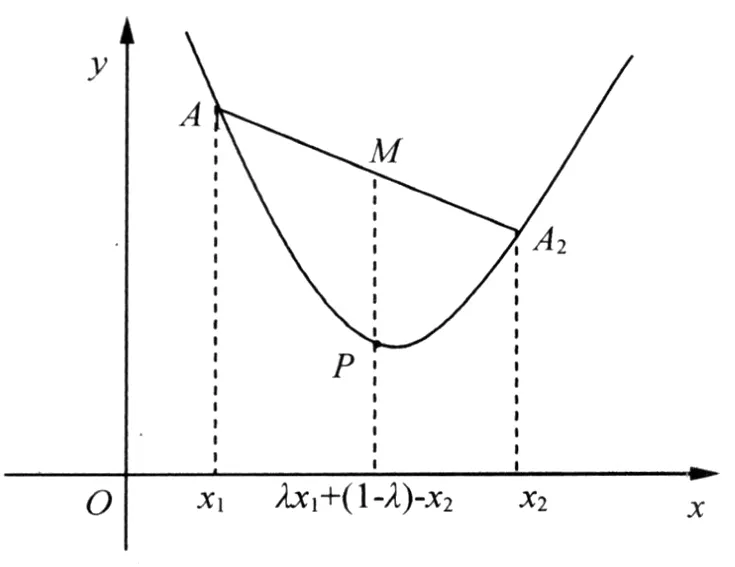
图3 Jensen不等式(n=2)

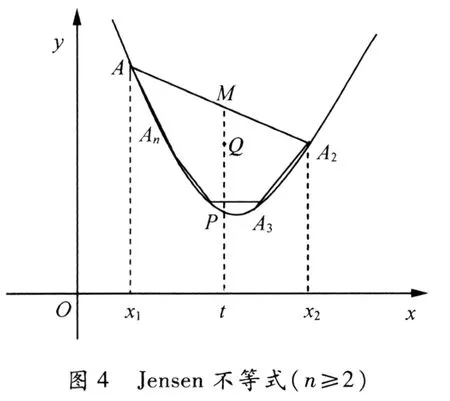
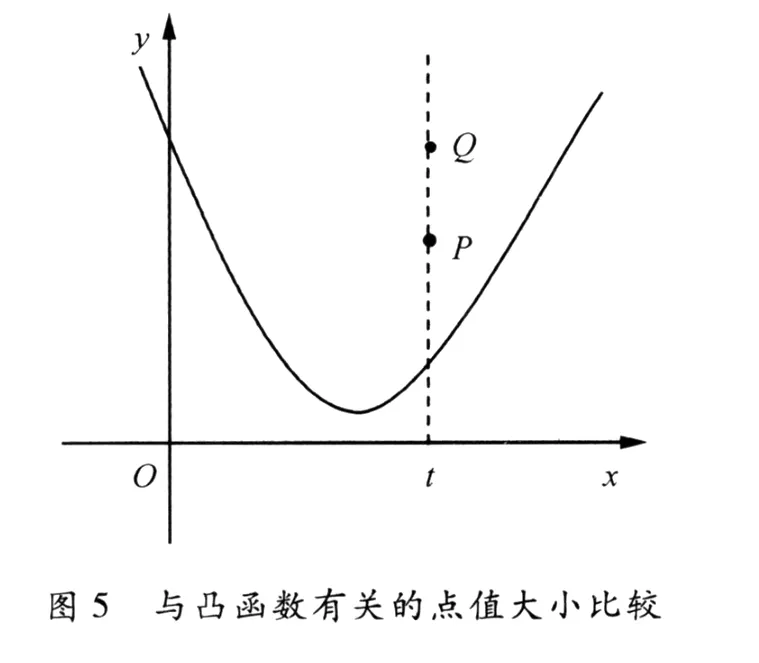
类似地,根据定理1,在图5中,我们可把P点看作顶点在凸曲线上的凸n边形中的点,Q点看作顶点在同一凸曲线上的凸2m边形中的点,则可得如下结论.

推论1 设f为区间I上的凸函数,若

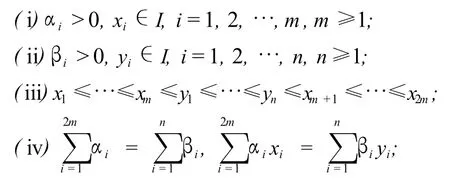
则有

成立,而对f为区间I上的凹函数,(3.3)式中的不等号反向.

特别地,设f为定义在实数集R上的凸函数,有

(1)取n=2,m=1,若x1≤y1≤y2≤x2,且α1x1+α2x2=β1y1+β2y2,α1+α2=β1+β2,α1,α2,β1,β2＞0,则

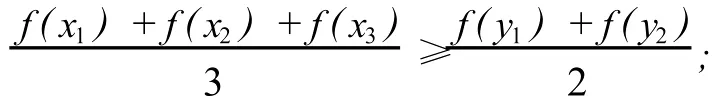
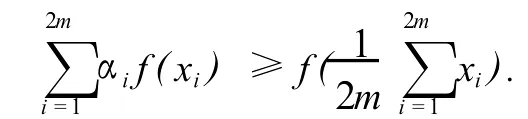
这些不等式有着广泛的应用[8].

3.3 用参数方程表示凸闭区域

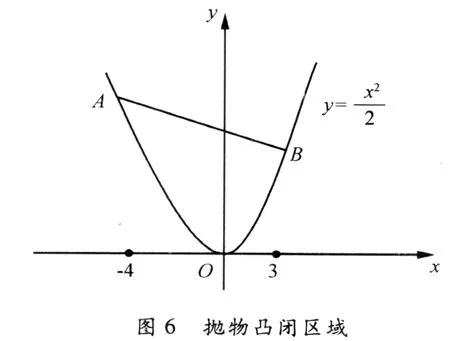
例4 用方程表示图6中的OAB闭区域.

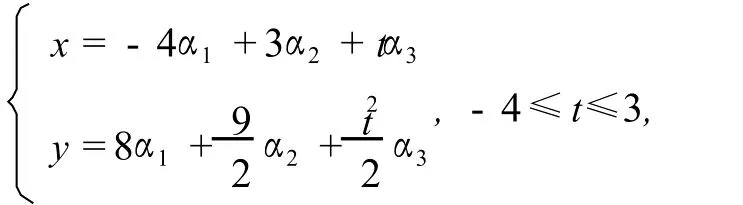
其中α1+α2+α3=1,且α1,α2,α3≥0.

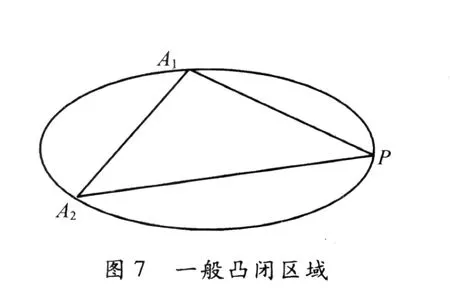
一般地,如图7所示,设A1,A2是凸闭区域边界上的两个定点,P是动点,则凸闭区域A1A2P的参数方程为

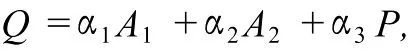
其中α1+α2+α3=1,且α1,α2,α3≥0(参数方程中的英文字母表示原点到字母的向量).

4 几个有待继续研究的问题

4.1 凸多边形外区域的参数方程问题

设三角形三个顶点坐标为A1(x1,y1),A2(x2,y2),A3(x3,y3),由于三角形闭区域表示方法是唯一的,所以ΔA1A2A3外区域的参数方程为

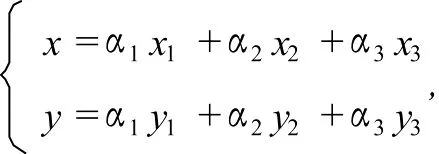
其中α1+α2+α3=1,且α1,α2,α3中至少一个为负数.

当n≥4时,由于凸n边形A1A2…An闭区域参数方程表示的不唯一,可推知凸n边形外区域参数方程表示也不唯一.如何确定满足

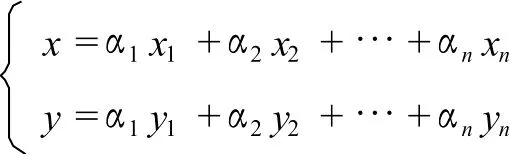
表示的是凸n边形的外区域,还有待进一步研究.

4.2 空间几何体的参数方程问题

作为本文定理的应用,还可以把结论推广到三维空间中.下文约定参数方程中的英文字母表示原点到字母的向量.

如对于底面是凸n边形A1A2…An的棱锥体,见图8,我们把棱锥体P-A1A2…An及其内部空间称为凸空间P-A1A2…An.

设Ai(xi,yi),1≤i≤n,n≥3,P(x0,y0),则由引理1及定理1可得凸空间P-A1A2…An的参数方程可表示为

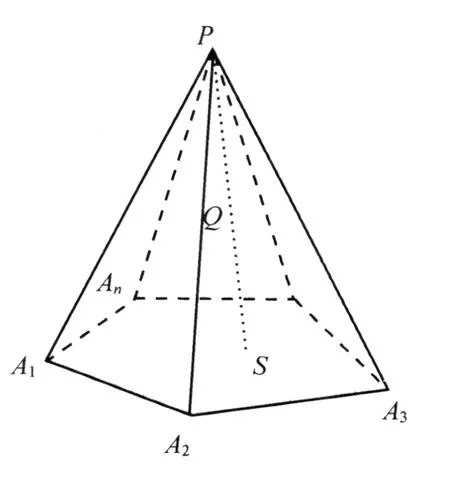
图8 凸n边形棱锥体

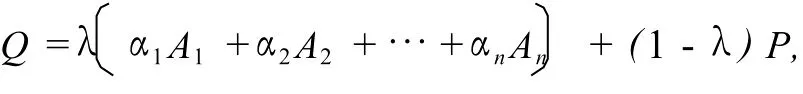
留下的问题是:对于一般的空间几何体,能否用参数方程表示它及其内容空间呢?

[1]肖运鸿.凸多边形区域的方程[J].赣南师范学院学报,1997(6):12-16.

[2]Prudnikov V Y.The Jensen Inequality in Ideal Spaces[J].Journal of Applied and Industrial Mathematics,2009,3(2):275-283.

[3]王玉芳,唐汝琴.Jensen积分不等式的应用[J].荆州师专学报:自然科学版,1988,21(5):16-18.

[4]胡学刚,韦艳利,胡春,等.Jensen加权不等式的几个推论与应用[J].内江科技,2007(3):32.

[5]陈欣.关于Jensen不等式的应用[J].武汉工业学院学报,2005,24(3):113-115.

[6]林铀.詹生(Jensen)不等式的推广[J].福州大学学报:自然科学版,1994,22(6):13-19.

[7]朱永娥.凸函数的一个性质与Jensen不等式[J].信阳师范学院学报:自然科学版,2007,20(4):399-400.

[8]李世杰.凸函数Jensen不等式的一个推广及其应用[J].抚州师专学报:自然科学辑刊,1988(3):30-37.