世博轴阳光谷结构风致响应分析及频域时域方法计算结果比较

韩志惠， 周晅毅，顾 明，张安安，张伟育，方 卫

(1.同济大学 土木工程防灾国家重点实验室，上海 200092;2.上海世博土控公司，上海 200125;

3.华东建筑设计研究院有限公司，上海 200002)

世博轴阳光谷结构风致响应分析及频域时域方法计算结果比较

韩志惠1， 周晅毅1，顾 明1，张安安2，张伟育3，方 卫3

(1.同济大学 土木工程防灾国家重点实验室，上海 200092;2.上海世博土控公司，上海 200125;

3.华东建筑设计研究院有限公司，上海 200002)

基于刚性模型风洞试验获得的建筑表面风压分布结果，分别采用频域和时域方法，对一个特大型复杂空间结构进行了风振响应计算。分析了结构的响应特性，并对两种计算方法得到的典型节点位移及单元轴力的均方根值、峰值及功率谱曲线进行了比较。结果表明，频域方法计算结果小于时域方法;两种方法计算的响应功率谱曲线反映了类似的能量分布;225°风向角是结构的最不利工况。

风致响应;频域方法;时域方法

近年来涌现出了许多造型新颖、极具现代感的空间结构，如上海铁路南站、国家体育场、国家游泳中心“水立方”等。这类结构一般跨度大、阻尼小，是典型的风敏感结构，风荷载是其设计的主要控制荷载之一，大跨空间结构的抗风研究一直是风工程领域中研究的热点问题。这类结构处于高湍流度的大气边界中，由于其复杂的外形，目前的荷载规范尚不能提供其表面的风压系数及风振系数，主要通过风洞试验和随机动力学计算来获得结构设计所需要的荷载［1，2］。

计算大跨空间结构的风致响应时一般包括频域和时域两种方法。顾明，周晅毅等［2］应用非定常风荷载试验加抖振响应计算的频域方法研究上海南站的风荷载和响应，计算中考虑多模态及模态之间的耦合效应。Yasushi Uematsu等［3］利用模态正交性对运动方程解耦，采用Newmark β法对模态坐标进行了时程分析。武岳，沈世钊等［4］利用非线性时程分析方法对弱非线性结构进行了风振分析，认为这类结构可以采用简化计算方法。频域计算方法中的模态叠加法是结构振动计算的常用方法，其概念清晰，计算简便，但这一方法主要适用于线性结构。时域计算方法建立在数值积分的基础上，可以较方便地考虑结构体系的非线性效应，直接反映结构在动力荷载作用下随时间变化的过程，缺点是花费的时间比较长。特别是对大型复杂结构，计算处理方法不同和误差常导致两种方法的计算结果存在一定差别。

为了对世博轴阳光谷这一大型复杂结构提供更为准确的抗风设计参数，在风洞试验数据的基础上，分别采用频域的模态叠加法和时域数值积分法来计算结构的线性风振响应。然后分析结构的响应特性，并对两种结果进行比较。本文简介计算方法和主要计算结果。

1 工程简介

世博轴工程是2010年上海世博会园区最大的单体工程，而“阳光谷”是世博轴建筑重要组成部分。世博轴中共有六个独立的单体阳光谷，排列位置如图1所示。阳光谷是由三角形网格组成的空间曲面单层钢结构体系，杆件截面高度为180 mm～500 mm，宽度为65 mm ～140 mm，杆件长度为 1.00 m ～3.5 m，面层为幕墙玻璃，整个结构仅在下部固定支承。每个单体形状略有不同，基本都呈上大下小的圆锥状，截面为变曲率的双曲面，形如盛开的喇叭花。限于篇幅，本文在下面的分析中仅选取阳光谷结构体系中第六个单体结构作为研究对象，下面简称“六号阳光谷”(图1中标号为6)。六号阳光谷位于结构体系端部，高约40 m，顶部最长轴约为90 m，最短轴约70 m，整体结构轻柔。由风洞试验结果可知，作用在该结构上的风荷载比其它阳光谷的荷载更大。其它阳光谷的风致响应特性和六号阳光谷类似。

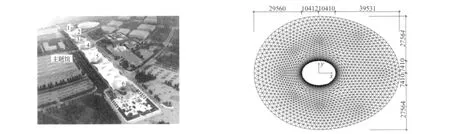
图1 世博轴效果图及六号阳光谷基本尺寸Fig.1 Picture of Expo Axis and size of Number Six sun-valley

2 风洞试验概况

世博轴刚性模型测压试验是在同济大学土木工程防灾国家重点实验室TJ－3大气边界层风洞中进行的(见图2)。试验模型用双层有机玻璃板和ABS板制成，具有足够的强度和和刚度，每个测点位置布置内外两个测压孔。模型的几何缩尺比为1/200，且考虑了实际建筑物和周边建筑之间的干扰情况。测点最终压力为内外表面测压孔压力之差，对于悬挑水平结构部分，压力作用向结构下表面为正，作用离结构下表面为负;对于竖直结构部分，压力作用向结构外表面为正，作用离结构外表面为负。为了准确获得结构表面风压间的相关性能，试验中采用了多通道同步测压技术，并对多信号的管路畸变进行了修正。

图2 风洞试验模型图和风向角定义Fig.2 Model for wind tunnel test and wind directions

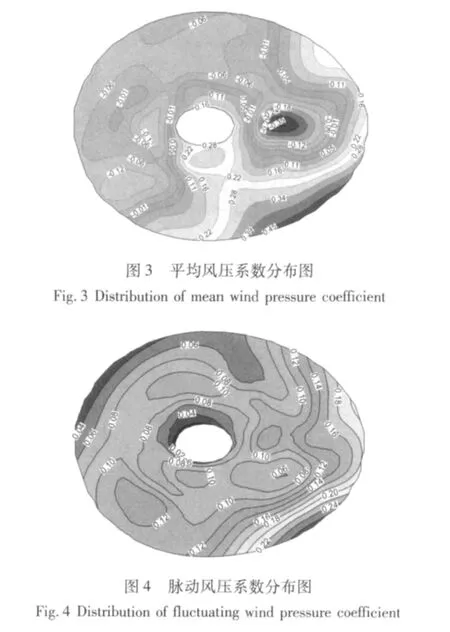
定义无量纲风压系数为测点压力与参考点压力的比值。风洞试验数据［5］显示，225°风向角(风向角定义见图2、图3、图4)是结构的最不利工况，限于篇幅，本文仅给出225°风向时的平均风压系数和脉动风压系数分布(见图3和图4)，而不给出其它风向的结果。详细的风洞试验结果见文献［5］。从图3和图4中可以看出，来流在结构顶部迎风侧严重分离，顶部迎风侧受吸力作用，平均风压系数为正。由于结构中间部分开口是由下至上逐渐增大，来流很快再附，导致结构表面出现大片的受压区，平均风压系数为负值。脉动风压系数较大的区域主要出现在结构顶部的迎风侧，变化梯度也较大，其它区域则相对较小。

3 风致响应计算方法

限于篇幅，这里不介绍平均风荷载作用下结构响应的计算方法，而只简单介绍结构抖振的计算方法。

3.1 频域计算方法(平稳激励下随机振动的模态叠加

法)

有限自由度结构体系在抖振荷载作用下的运动方程为:

利用平稳激励下线性系统随机振动的模态叠加法［6］，位移响应功率谱密度矩阵可由下式计算:

其中［H］为传递函数矩阵，［Φ］为振型矩阵，［Spp(ω)］为力谱矩阵。式(2)为精确的CQC(Complete Quadratic Combination)计算公式，包括了所有振型交叉项，考虑了振型之间的相互影响。基于上述理论，本课题组编制了动力计算程序SWDP，可以方便地计算结构的各种响应。

3.2 时域计算方法

时程分析法就是对运动方程进行直接积分，仅在一系列离散的时间点上求运动方程的解。本文基于商业有限元软件平台，将风荷载时程作为外荷载作用于有限元模型上，采用Newmark逐步积分法和Newton-Paphson迭代理论，得出结构的动力响应。

结构的运动平衡方程为:

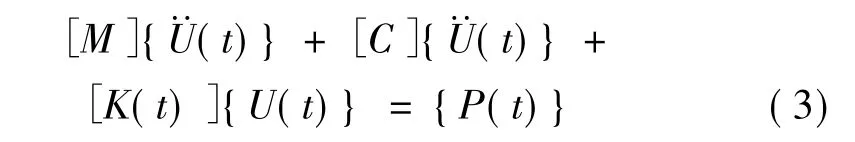
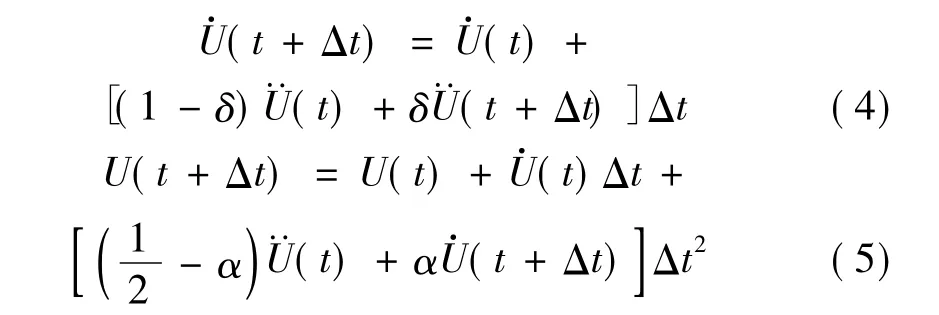
利用式(4)、式(5)将运动微分方程转化为代数方程，采用Newton-Paphson迭代法进行循环迭代，最终可得到结构在风荷载作用下的响应时程。

4 风振响应计算结果

图5 结构振型Fig.5 Mode shapes of structure

4.1 结构振型分析

六号阳光谷结构的第1阶自振频率为0.771 Hz;在0.771 Hz到3.084 Hz之间，存在40 阶频率，振型分布密集。图5为结构的前6阶振型。图中可以看出，结构振动都以悬挑边的竖向振动为主，且较长悬挑边振动幅度相对更大一些。这说明悬挑边是整个结构中最薄弱的部分，且随着阶数的增加，悬挑边上的波数也越来越多。

4.2 计算参数选取

结构响应的计算参数为:(1)地貌类型:C类;(2)基本风压:0.55 kPa(50年重现期);(3)结构阻尼比:ζ=0.02;(4) 频域积分步长 Δf=0.006 7 Hz，参振模态:第1～50阶模态;(5) 时域积分步长Δt=0.072 6 s，阻尼常数:α =0.126 8，β =0.003 1。

4.3 时域和频域方法获得的结构响应的比较

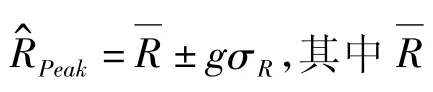
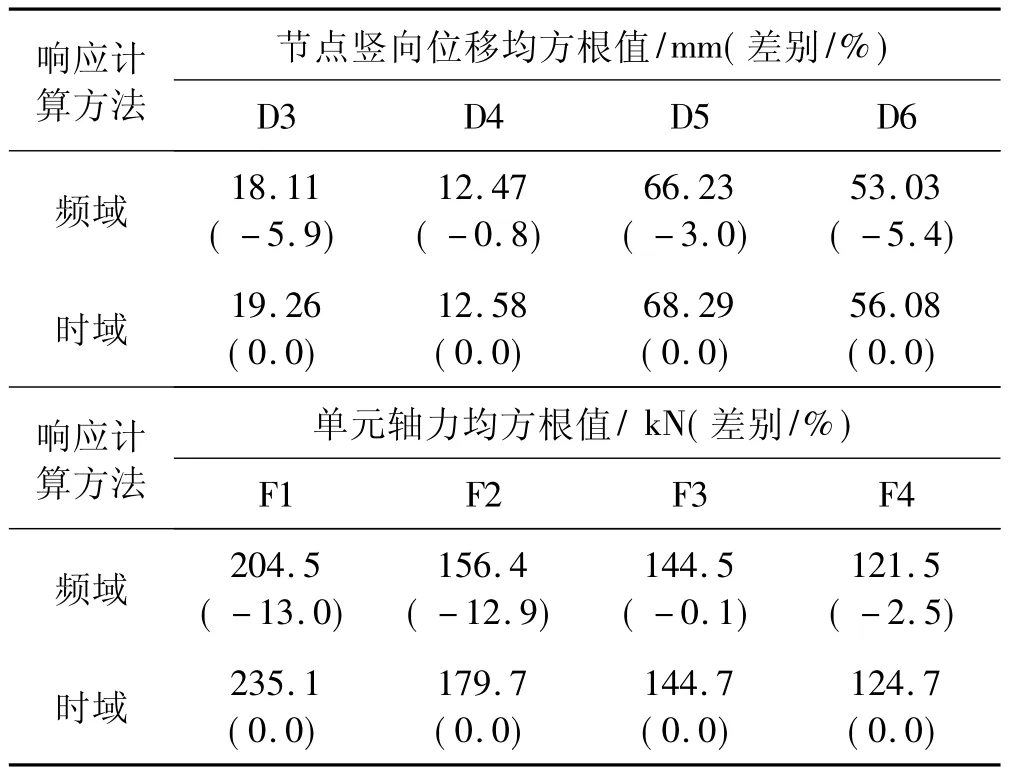
表1 响应均方根值对比(225°风向角)Tab.1 Comparison of RSM values(225°wind direction)

表2 响应峰值对比(225°风向角)Tab.2 Comparison of peak values(225°wind direction)

图6为225°风向角下动力响应较大的节点D5、D6和单元F1、F2的响应功率谱对比结果。两种方法都反映出脉动风荷载激发了相同的模态。对于节点D5、D6，共振能量主要由第1、2、3、4阶振型提供，由于第1、2阶频率和第3、4阶频率值相差很小，故图中只出现两个峰值。而对于单元F1、F2，第3、4阶振型是其能量的主要提供者，第1、第2阶振型提供能量相对较小。响应功率谱曲线显示时域方法计算的功率谱数值要大于频域方法，这也是上文中时域方法计算的响应均方根大于频域计算结果的原因。定义共振部分能量与总脉动能量的比值为σ2R/σ2，其中σ2R为共振部分的响应方差，σ2为总脉动响应方差。图7给出共振部分能量与总脉动能量的比例关系，可以看出对于位移响应，共振部分能量和背景部分能量各自约占总脉动能量的50%左右;而对于轴力响应，共振部分所提供的能量都在60%以上，大于背景部分。

4.4 节点位移响应和单元轴力响应随风向变化规律

上文分析可知，虽然频域计算方法结果小于时域计算方法，但是频域计算方法省时简便，且两者差别不大，故本文给出频域方法得到的典型节点和单元响应随风向的变化规律。节点D1～D6和单元F1～F4位置如图2所示。图8分别为节点的竖向位移响应和单元轴力响应的平均值、以及应用频域方法得到的均方根值、峰值随风向角的变化情况。

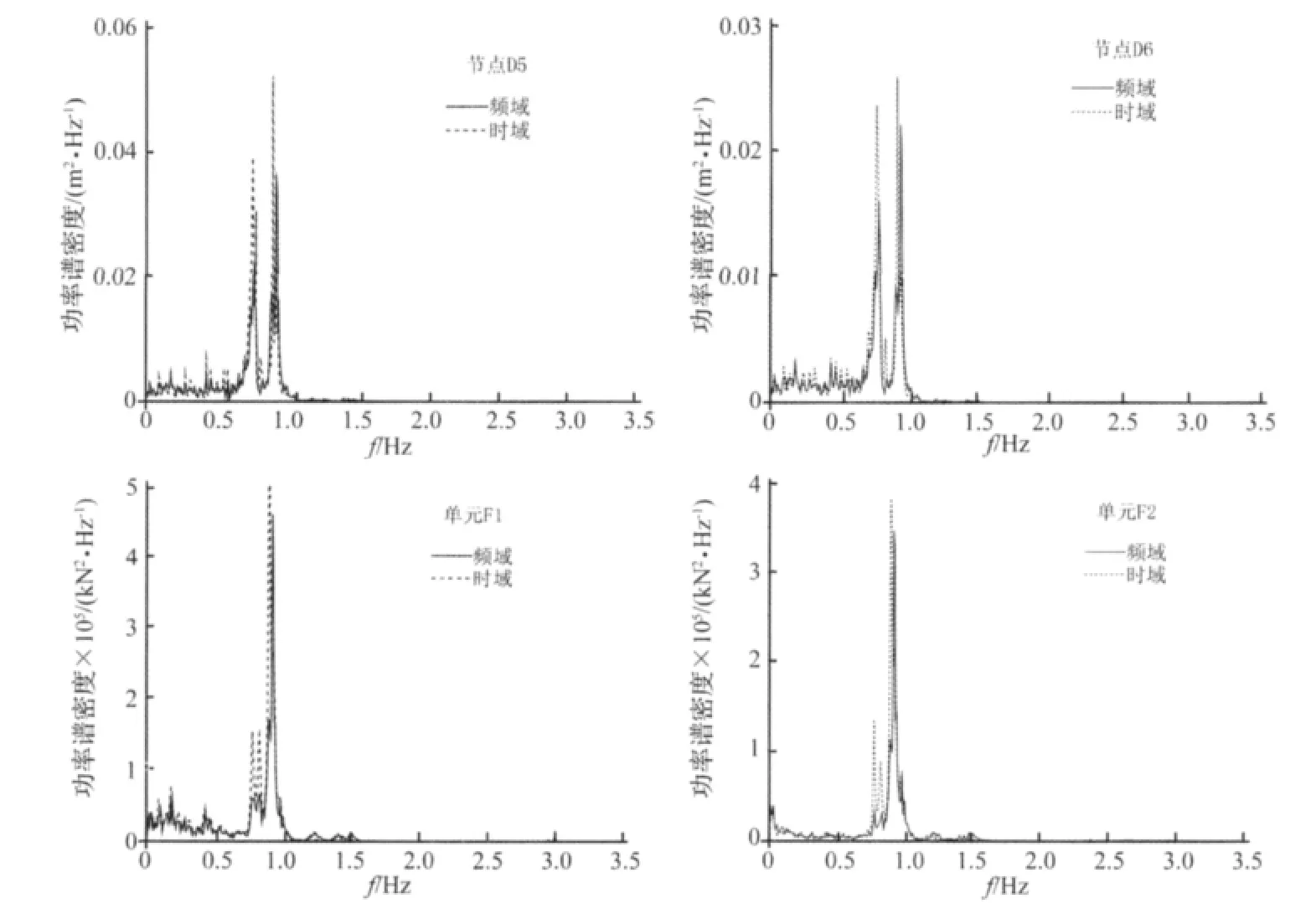
图6 节点和单元响应功率谱曲线对比Fig.6 Comparison of power spectral density of typical nodes and elements

图7 共振部分能量与总能量比例关系Fig.7 Ratio of resonant component energy to total energy

竖向位移响应显示，在来流作用下，位于迎风侧的节点向上运动;位于背风侧的节点向下运动。节点D1、D2、D5、D6分别位于迎风侧时(分别对应图中45°、135°和225°风向角)，其位移平均值出现极大值。这是因为来流经过结构时，在顶部迎风侧发生分离，迎风前缘受到较大的吸力作用，加之结构的长悬挑边刚度相对较小(参见图5)，作用荷载的整体效果导致迎风侧竖向位移较大。节点D3、D4由于受到前方建筑物“主题馆”(见图1)的阻挡，其位移平均值并没有在315°风向角(没有遮挡时的正迎风位置)下出现极大值，而是出现在0°风向下。此外，这些点的均方根值极值全部出现在225°风向下。所以，可以认为225°风向角是结构位移响应的最不利工况。此工况下，节点D5由于位于悬挑边的最外边且受到正面迎风作用，其位移均方根值最大，是位移响应的控制点。

由轴力响应结果可知，单元轴力平均值分别在45°、135°和225°风向角下的出现极值，且135°风向角下的响应较大。但是225°风向角下，单元F1的均方根值出现极值，峰值达到－818KN(压力)。可以认为，对应于结构位移响应，结构轴力响应的最不利工况也是225°风向。

5 结论

本文基于风洞测压试验结果，用两种方法对世博轴阳光谷结构进行了风致抖振响应计算，分析了结构的响应特性，并比较了两种方法计算得到的响应结果，得到主要结论如下:

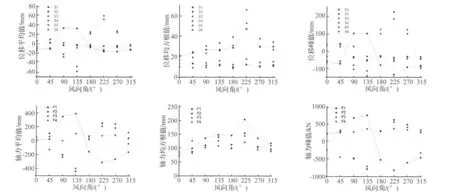
图8 节点和单元响应随风向变化的曲线Fig.8 Responses of typical nodes and elements as a function of wind direction

(1)频域方法计算的响应均方根值和峰值小于时域方法，轴力的计算差别大于位移。

(2)对于位移响应，共振部分能量和背景部分能量各自约占总脉动能量的50%左右;而对于轴力响应，共振部分所提供的能量在60%以上。两种方法计算的响应功率谱反映了类似的能量分布，说明共振能量主要由前四阶振型提供。

(3)极大值位移出现在结构顶部迎风侧，此时风向为225°;单元轴力响应均方根值极值也出现在225°风向。225°风向角是结构的最不利工况。

［1］顾 明，黄 鹏，周晅毅，等.北京首都机场3号航站楼风荷载和响应研究［J］.土木工程学报，2005，38(1):40－44.

［2］顾 明，周晅毅，黄 鹏.大跨屋盖结构风致抖振响应研究［J］.土木工程学报，2006，39(11):37 －42.

［3］ Uematsu Y，Watanabe K.Wind-induced dynamic response and resultant load estimation of a circular flat roof［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，83，251－261.

［4］武 岳，郭海山，陈新礼，等.大跨度点支式幕墙支承结构风振性能分析［J］.建筑结构学报，2002，23(5):49－55.

［5］顾 明，周晅毅，等.世博轴及地下综合体工程抗风研究风洞试验和响应计算［R］.同济大学土木工程防灾国家重点实验室，2007.

［6］俞载道，曹国敖.随机振动理论及其应用［M］.上海:同济大学出版社，1988.

Analysis＆comparison of wind-induced responses of sun-valley structure of expo axis using frequency and time domain methods

HAN Zhi-hui1，ZHOU Xuan-yi1，GU Ming1，ZHANG An-an2，ZHANG Wei-yu3，FANG Wei3

(1.State Key Laboratory for Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China;2.Shanghai World Expo Land Holding Co.Ltd，Shanghai 200125，China;3.East China Architectural Design and Research Institute Co.Ltd，Shanghai 200002，China)

Based on wind pressure data from wind tunnel tests，the wind-induced responses of sun-valley structure of Expo Axis were calculated both in frequency domain and time one.Then，the characteristics of the wind-induced responses were analyzed.The RSM values，the peak values and the power spectral density of some typical displacements and element axial forces obtained with two different methods mentioned above were compared.The results indicated that the RSM values computed in frequency domain are smaller than those in time domain;the comparison of power spectral density curves shows similar energy distributions;the most unfavorable condition is 225°wind direction.

wind-induced response;frequency domain method;time domain method

TU312

A

国家科技支撑计划世博科技专项(2009BAK43B06);上海市科学技术委员会科研计划项目世博科技专项(08dz0580305)

2010－01－04 修改稿收到日期:2010－03－09

韩志惠 女，博士生，1985年生