长周期结构地震瞬态反应研究

吴 琛，周瑞忠

(1.福建工程学院 土木工程系，福州 350108;2.福州大学 土木工程学院，福州 350108)

长周期结构地震瞬态反应研究

吴 琛1，周瑞忠2

(1.福建工程学院 土木工程系，福州 350108;2.福州大学 土木工程学院，福州 350108)

传统动力学理论通常认为地震瞬态反应可以忽略。基于简谐地震反应的基本理论，引进小波包分解技术，推导了实际地震动作用下，多自由度体系瞬态反应的计算方法。分析了等效单自由度体系的反应谱特性以及瞬态振动的规律。明确了长周期结构的最大位移可能出现在结构瞬态振动中，其值甚至超过结构在地震激励期间所发生的共振位移。通过实际地震动作用下长、短周期结构瞬态反应的比较，表明短周期结构主要由稳态振动控制，而长周期受瞬态振动影响显著。因此，长周期结构抗震不仅要避免共振发生，还须充分考虑到结构瞬态振动的位移破坏。

振动与波;长周期结构;瞬态反应;小波包分析;反应谱

传统的结构动力学理论［1］认为，由于阻尼的影响，由自由振动和伴生自由振动构成的瞬态自由振动随时间很快就消失了，因此通常不予讨论，而只强调稳态振动的作用。关于这一点，近期的研究［2－4］以简谐荷载为输入，经位移解析解分析认为，当激震频率相对结构自振频率较大时，瞬态自由振动可以引起结构很大的位移反应，因而对于长周期高柔结构或基础隔震结构而言，瞬态振动不能被简单地忽略。

简谐震动的位移解析解为地震瞬态反应的研究提供了理论基础。但在工程实践中，研究结构的实际地震反应才更具有实用价值。问题的难点在于:实际地震动是一种典型的宽频带非平稳信号，地震反应无法如简谐荷载般用解析解来表示。当采用数值计算时，所得的计算结果为全解，无法区分瞬态反应与稳态反应，因此结构的地震瞬态反应在计算方法上具有一定的难度。本文将利用小波包分解［5］可将任意宽频带信号分解成若干个窄带频率成分之线性叠加的强大功能，以简谐地震反应为理论基础，实现长周期结构在实际地震作用下的瞬态反应计算与分析。

1 地震瞬态反应的解析数值求法

为利用简谐波瞬态反应的解析法求解，现将地震动通过小波包分解成若干个频率的线性叠加。对每个分量按照小波包系数进行线性调幅，从而将各分量拟合成简谐波。于是，在小波空间内可建立k振型等效单自由度体系的简谐振动方程:

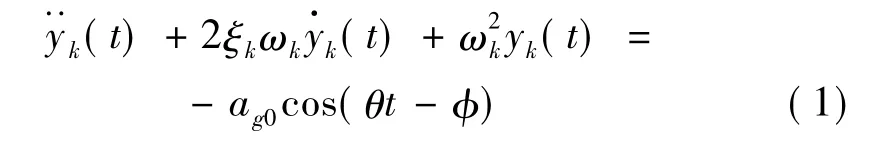
经推导，方程(1)的k振型等效单自由度体系位移yk(t)由三部分组成:

至此，小波空间内等效单自由度体系在拟合简谐波作用下的瞬态反应yk1(t)+yk2(t)已得解，进而通过一次线性调幅的逆过程即可实现小波空间到物理空间的映射。然后将各小波包分量产生的分项位移进行线性叠加，即可获得等效单自由度体系的瞬态反应与稳态反应。

对于弹性多自由度体系而言，其动力计算可利用各振型相互正交的特性转化为若干个等效单自由度体系的问题。于是，N自由度体系i质点的瞬态位移xti(t)和稳态位移xsi(t)可分别表达为:

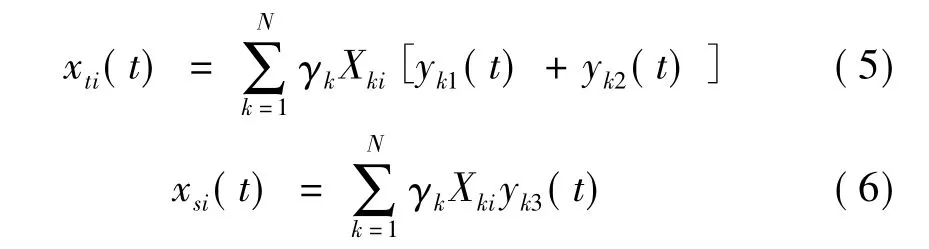
其中γk为第k振型的参与系数，Xki为振型幅值。

2 等效单自由度体系瞬态反应分析

现以福州地区一座基本自振周期T1=2.10 s的27层长周期结构为例分析瞬态反应对长周期结构的影响。输入峰值为35 gal的Taft波，持时10 s，将其经过8层“db4”小波包分解，并利用小波变换可安全有效地滤去地震动超高频成分，提高信噪比的特点［6］，选取其中前30个分量参与计算，这30个分量经重构后仍能较好地反映原始地震波的基本特性，如图1所示。

2.1 等效单自由度体系反应谱研究

图1 Taft地震波及小波包分量重构信号Fig.1 Taft earthquake and the reconstructed signal by wavelet packet components

抗震设计所关注的主要是结构在地震作用下的最大反应，反应谱恰好表现出了这一要求，至于最大反应究竟发生在结构的稳态振动阶段还是瞬态振动阶段，当采用传统的数值计算方法时并不明确。在本文解析数值解法的基础上，现以结构第一自振周期T1与小波包分量振动周期Tg之比为横坐标，分别绘制等效单自由度体系位移全解、瞬态解和稳态解的反应谱图，见图2。

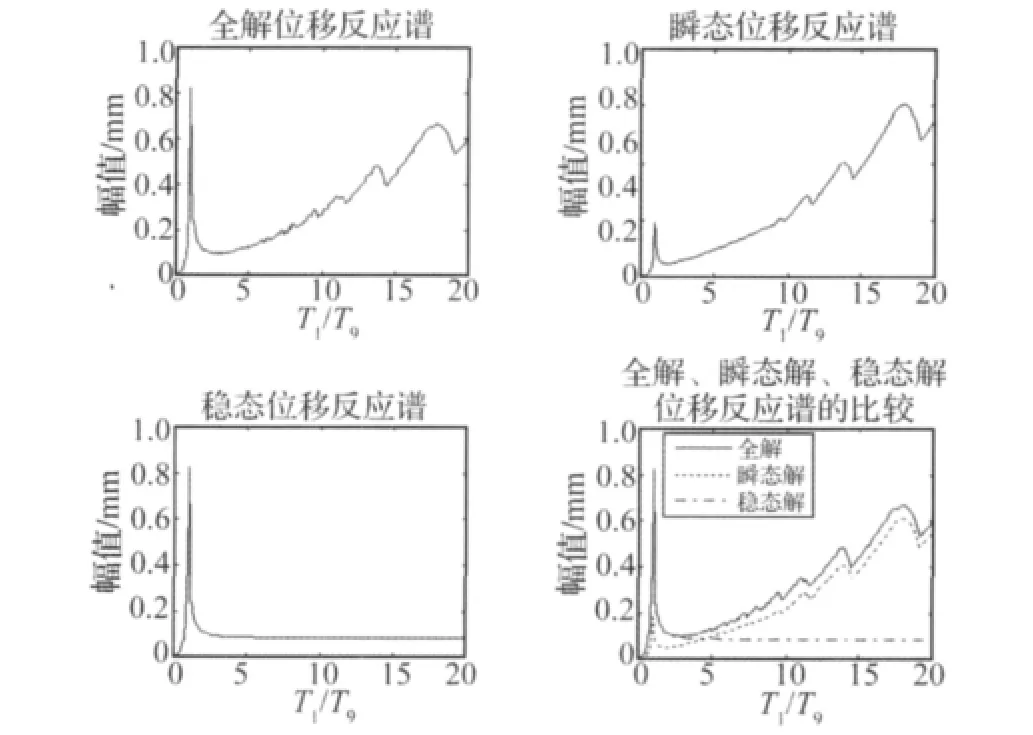
图2 等效单自由度体系位移全解、瞬态解、稳态解反应谱Fig.2 Response spectra of equivalent SDOF system for complete solution，transient solution and steady state solutions

由图可见:

(1)三类反应谱均在共振区出现峰值，这与动力学及抗震理论的共振原理完全相符。

(2)全解反应与瞬态反应在长周期段的最大位移随结构基本自振周期的增长而增大，当T1≫Tg时，结构的最大位移甚至可超过共振体系的最大位移。可见，大位移不仅可能发生在共振体系中，还可能发生在外载频率较高，结构基本自振频率较低的长周期体系中。

(3)在长周期段，瞬态反应谱的形态与全解反应谱大致相同，而稳态反应谱则趋于一个小值常数，说明了当地震动高频分量极为丰富时，长周期结构的最大位移往往出现在结构的瞬态振动阶段，因而必须充分考虑到瞬态反应对长周期结构的影响。

2.2 等效单自由度体系瞬态反应计算与分析

为讨论外载频率较高时长周期体系瞬态振动的影响，现在30个小波包分量中，选取周期Tg≈0.32 s的高频分量作用于上述长周期结构各振型对应的等效单自由度体系，按本文方法计算其位移瞬态解与稳态解。图3显示了第1、3、5阶等效单自由度体系的计算结果。为验证本文推导公式(2)～(4)之正确性，将瞬态与稳态振动叠加之总位移与Duhamel积分数值全解进行了比较。

图3 第1、3、5阶等效单自由度体系位移瞬态解、稳态解、全解及Duhamel积分数值解Fig.3 The transient solution，steady state solution and complete solution of No.1，No.3＆No.5 equivalent SDOF syst

由该图可见:

(1)本文所提供的解析数值法能有效地从位移全解中区分出瞬态与稳态振动，二者叠加后与Duhamel积分结果基本吻合，说明该方法是有效的。

(2)当地震动高频分量作用于第一振型时，等效单自由度体系的瞬态反应幅值较大且衰减缓慢，总位移的形态与幅值更接近于瞬态振动。可见，当高频地震动作用于低阶振型(Tj≫Tgi)时，该等效体系的位移主要受控于瞬态振动。

(3)当地震动高频分量作用于第三振型时，瞬态解约在4 s处衰减完毕，4 s内瞬态振动对于总位移的影响不可忽略，同一时刻稳态位移与总位移在方向以及幅值上的差异正是由于瞬态振动的存在引起的;当地震动高频分量作用于第五振型时，瞬态解约在1.5 s处就衰减完毕，说明此时瞬态振动对总位移的贡献几乎可以忽略。可见，随着振型阶次的提高，瞬态反应的衰减越来越快，位移的振动由受瞬态反应控制逐渐转变为受瞬态与稳态振动的共同影响，最后转变为受稳态振动控制。由于低阶振型特别是第一阶振型为结构振动提供了最主要的能量［7］，因此当激震频率较高时，长周期结构受瞬态反应的影响是很大的。

抗震基本原理［8］认为:由于地震波在由震源向外扩散传播时，高频分量衰减快而低频分量衰减慢，因此当长周期柔性建筑物处在大地震、远震中距时，易与低频地震动分量产生共振，其震害往往要比处于中小震级、近震中距时严重。然而在近年来的几次大地震中，近场地震动对长周期结构都产生了不同于理论的显著影响。通常我们将这种现象归因于近场地震动中的低频分量对长周期结构产生了共振［9］，但经过以上分析，还必须注意到，在近断层场地，地面结构主要受到地震动中体波的影响。体波中含有丰富的纵波和横波分量，其中纵波的周期短，振幅小，而横波的周期较长，振幅较大。尽管振幅较小的纵波本身不会使结构产生较大的位移反应，但如果再与横波造成的结构位移反应进行叠加，那么高频分量丰富的体波对地面结构的位移反应影响将是十分显著的。

3 长、短周期结构瞬态反应比较

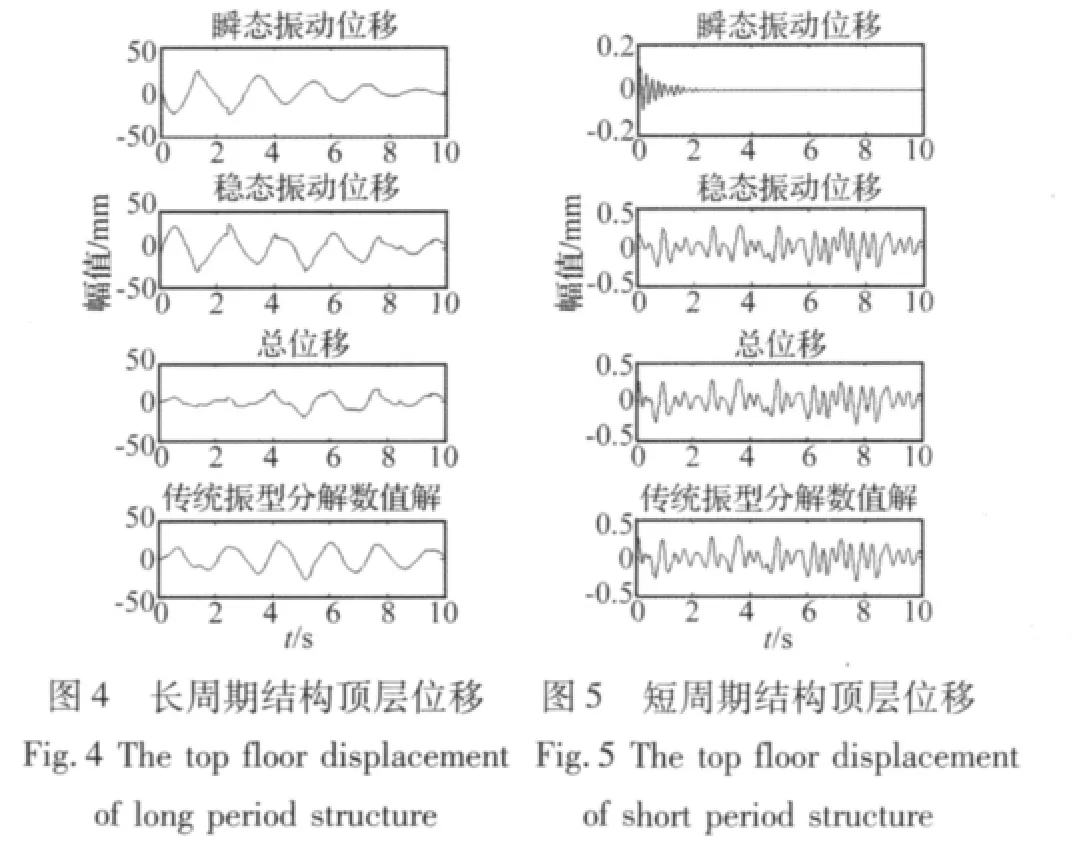
现将峰值为35 gal的Taft波分别输入上述基本自振周期T1=2.10 s的27层长周期结构和一座T1=0.22 s的3层短周期结构中，按本文方法分别计算长、短周期结构在实际地震动作用下的顶层瞬态反应与稳态反应，并将叠加后的总位移与传统振型分解法进行比较，见图4、图5。

如图可见:

(1)采用本文所述的解析数值法进行结构地震反应计算，由瞬态振动和稳态振动叠加之总位移与传统振型分解法的结果是相近的，说明采用本方法讨论结构瞬态振动的影响是可行的。

(2)在实际地震动作用下，短周期结构的瞬态振动因阻尼的存在而迅速衰减，顶层位移的形态与幅值更接近于稳态解，说明短周期结构的振动主要由稳态反应控制，正如动力学理论所述，此时瞬态反应可以不考虑;但在长周期结构的振动中，瞬态振动对于结构变形的形态、幅值、方向都起着至关重要的作用。特别是对于考虑了基底隔震的结构，其周期远大于原基础固定结构的周期［10］，因而，瞬态反应在总地震反应中的作用是不可忽略的。

4 结论

(1)本文利用小波包分解将地震信号分解成有限窄带信号，并通过线性调幅拟合简谐波形，借助简谐地震反应解析解实现等效单自度体系瞬态反应与稳态反应的分离，最后通过振型叠加及小波包分量叠加，求得结构在实际地震动作用下的分项位移，这一方法为地震瞬态振动的研究奠定了基础。严格说来，幅值调整和线性叠加等方法只适合于线性时不变系统。但基于结构地震反应的分项定量计算目前尚无其他计算方案可资比较，并且非线性弹性阶段仍可以用分段线性作为计算依据，因此，本文方法仍具有较大的工程实用意义。如何进一步增强对非线性反应的适应性、实现在实际工程中的合理应用将是我们下一步的工作，以期真正对工程设计有所裨益。

(2)从等效单自由度体系的反应谱来看，对于基本自振周期远大于激震卓越周期的长周期结构而言，最大反应不仅可能发生在共振情况下，还可能发生在自由瞬态振动阶段。因此，长周期结构抗震不仅要避免共振发生，还须充分考虑到瞬态自由振动阶段的位移破坏。

(3)在高频分量丰富的体波作用下，长周期结构振动主要受控于瞬态振动，随振型阶次的提高，位移的振动逐渐由受瞬态反应控制过渡到受稳态振动控制。由于低阶振型为结构振动提供了最主要的能量，因此，高频分量引起了长周期结构很大的位移，该位移甚至超过结构在地震激励期间所发生的共振位移，这是除共振外，近场地震动频频引发中心城市高层建筑破坏的重要原因之一。

［1］Chopra A K.Dynamics of structures:Theory and applications to earthquake engineering［M］.Prentice Hall:Englewood Cliffs，NJ，1995.

［2］祁 皑，范宏伟，陈永祥.简谐荷载作用下伴生自由振动的研究［J］.地震工程与工程振动，2002，22(6):156－161

［3］祁 皑，范宏伟，陈永祥.简谐地面运动作用下系统瞬态振动的研究［J］.振动、测试与诊断，2003，23(3):199－201.

［4］徐龙军，谢礼立，郝 敏.简谐地震动反应谱研究［J］.工程力学，2005，22(5):7－13.

［5］ Ingrid Daubechies.Ten Lectures on Wavelets［M］.SIAM，Philadelphia，PA，1992.

［6］吴 琛.小波分解法在多自由度线性体系地震反应分析中的应用［J］.福建工程学院学报，2008.6(3):213 －218.

［7］吴 琛，周瑞忠.基于小波变换的结构地震响应与能量计算分析［J］.地震工程与工程振动，2006，26(6):24 －30.

［8］Rosenbueth E.Design of Earthquake Resistant Structures［M］.London:Pentech Press Ltd，1980.

［9］Hall J F，Heaton T H，Halling M W，Wald D J.Near-source ground motions and its effects on flexible buildings［J］.Earthquake Spectra，1995，11(4):569－605.

［10］ Skinner R I，Robinson W H，McVerry G H.An introduction to seismic isolation［M］.Chichester:Elsevier Science Ltd，1995.

Earthquake transient response of a long period structure

WU Chen1，ZHOU Rui-zhong2

(1.Department of Civil Engineering，Fujian College of Technology，Fuzhou 350108，China;2.College of Civil Engineering，Fuzhou University，Fuzhou 350108，China)

The transient response of a structure is usually ignored in traditional dynamic analysis.Based on the theory of harmonic earthquake response and wavelet packet analysis，the transient vibration of a MDOF system subjected to real earthquake ground motion was studied.Response spectra and transient vibration rules of the equivalent SDOF system were analyzed.It was concluded that the maximum displacement of a long period structure may occur in transient vibration and its value is greater than its resonance displacement.By comparing the transient response of a long period building with that of a short period one，it was shown that short period structures are mainly controlled by steady state vibration and the effects of transient vibration on a long period structure is prominent.Therefore，transient displacement and resonance one should be considered in earthquake-resistant design of long period structures.

vibration＆wave;long period structure;transient response;wavelet packet analysis;response spectra

TV312

A

福建省自然科学基金资助项目(2010J05103);福建省教育厅A类科研项目(JA08173);福建工程学院引进人才科研启动基金项目(GY－Z0804)

2009－09－08 修改稿收到日期:2010－03－29

吴 琛 女，博士，1978年生