刚性转子自动平衡寻优控制方法与实验研究
黄立权,王维民,苏奕儒,李 燕,高金吉
(北京化工大学 诊断与自愈工程研究中心,北京 100029)
刚性转子自动平衡寻优控制方法与实验研究
黄立权,王维民,苏奕儒,李 燕,高金吉
(北京化工大学 诊断与自愈工程研究中心,北京 100029)
在线消除转子系统的振动对保证旋转机械的可靠和高效运行是至关重要的。在转子振动控制初期,需要一个试探性的控制力,该力可能会使系统振动加剧或减小,这取决于控制力与原激振力相位之间的关系。为此该研究在转子系统动力学及电磁力可控特性分析的基础上对控制力相位进行区域划分,建立系统寻优控制模型并提出具体寻优策略;采用有限元分析的方法获取工作转速下转子系统理论滞后角,初步确定控制力相位;以此相位值作为寻优参数起始值,按照既定寻优策略实现转子自动平衡控制,并确保控制全过程转子振幅不大于初始不平衡故障振幅;最后建立实验台并对算法进行实验验证,结果表明该方法是有效的。
电磁力;自动平衡;自愈调控;有限元分析;寻优控制
工业生产中,旋转机械不平衡故障振动导致的停产事故通常会造成巨大的经济损失。该类故障可采用动平衡技术进行消除,但动平衡技术工作量大,效率低,且需熟练的平衡技巧[1]。因此,研究一种能够在线抑制振动的控制策略,实现故障的自愈调控,具有重要的理论意义和工程应用价值[2]。
随着技术的发展,旋转机械对自动平衡控制技术提出了更高的要求,比如更快的控制响应速度,更高的控制精度等。通常情况下,不平衡振动对旋转机械而言是一种有害运动,在振动控制的初始试探阶段,由于试探控制力相位选取不当可能会导致振动加剧,从而带来不良后果。所以在满足高精度和快速性等控制要求的情况下,避免振动加剧的控制要求也应给予考虑。也即稳定工作状态时,在转子故障振动的基础上施加控制后,确保对应振动响应幅值在控制时域内不大于转子原始故障振动幅值。随着电磁技术的进步,电磁作用力式平衡装置[3]在转子平衡领域的应用研究有所发展,其平衡原理是向转子提供可控的旋转矢量电磁力来克服激振力。电磁力的可控特性为转子振动无加剧控制的实现提供了可能。
基于此,本研究提出在电磁作用力式平衡装置的基础上,采用寻优算法与有限元[4]转子动力学分析相结合的方法,实现转子自动平衡,且确保控制过程中转子振动不大于原始故障振动幅值。最后在实验台上进行实验验证,研究结果表明该方法是有效的。
1 系统动力学模型分析
设有一转子轴承系统,原有不平衡激振力为{Fu},
引入电磁控制力{Fc}后系统运动方程为[5]:

系统引入的电磁控制力由电磁轴承产生,也有文献称该类型装置为电磁式作动器[6]。图1所示为电磁作用力式平衡装置所在系统的第i个截面上电磁力与不平衡激振力作用示意图。

图1 电磁力执行装置及作用力示意图Fig.1 Electromagnetic actuators and force diagram
在该截面处转子的动力学模型可描述为:

式中Fui为工作转速下,由系统在截面i处的当量不平衡质量m在离转子几何中心r处引起的不平衡激振力;Fci为电磁平衡控制力;i为激振力和控制力所在的力学模型中的节点编号。
电磁力是被控对象位移和控制电流的非线性函数[7],其线性化公式如下所示[8]:

式中ki和kx为电磁系统参数。在本系统中,电磁平衡装置不承受静态载荷,(3)式可简化为:

将式(4)代入式(2)并移项整理得到下式:
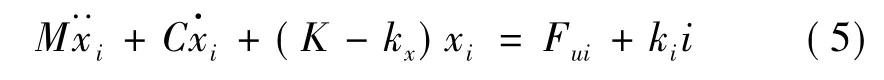
上式中kii表示由磁极线圈控制电流产生的电磁力,可记为Fci(i),则上式转化为:

式中K*为总刚度。为叙述方便,Fci(i)仍然记为Fci。在图1所示的示意图上,将x方向的电磁线圈中的控制电流记为ix,y方向线圈中的控制电流记为iy,则磁极线圈控制电流可表示为下式:

i表示磁极线圈电流,对应Ii为电流幅值,φi为初始相位。显然如果能够协调控制磁极线圈的电流,则可实现对电磁力大小、方向和旋转速度的控制。对应控制电磁力表达式以及系统不平衡激振力为:

线性系统满足叠加原理,转子系统界面i处的稳态振动响应为:

式中zui和zci分别为转子节点i处由不平衡激振力Fui和控制力Fci引起的振动响应。不平衡振动消除的本质是不平衡力的消除,显然转子不平衡振动的抑制,可通过对激振力的消除来实现。通过上面的理论分析可知,利用可控电磁力消除系统不平衡激振力来实现不平衡振动抑制的方法是可行的。
2 控制系统及转子不平衡振动调控方法
2.1 控制力相位区域划分
在转子振动在线控制初期,需要一个试探性的控制力,这个力可能会使系统原始故障振动加剧或者减小,这取决于控制力与不平衡激振力相位之间的关系,为此对控制力相位进行分析如下。

图2 系统作用力平衡示意图Fig.2 System force balance diagram
图2所示为系统作用力平衡示意图。在不影响控制精度的情况下,依据工程经验,试探控制力幅值按照下式选取:
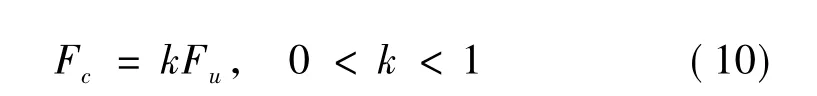
Fu为系统不平衡激振力,Fc1、Fc2、Fc3为图2中所示幅值相等而相位不同的试探控制力。
β为控制力Fc与不平衡激振力Fu的夹角,

为便于分析,规定控制力对转子原始振动起加剧作用的相位区域为负作用区,用N(negative)表示,对应区域大小为(0,β*)∪(2π - β*,2π),φN为 N 区域内相位角;控制力起抑振作用的相位区域为正作用区,用P(positive)表示,对应区域大小为(β*,2π -β*),φP为P区域内相位角,显然最佳控制力相位φ*P必定位于P区。在相位β*处,控制力对振动抑制作用的贡献为零,故可称β*为非调相位;同理φ*P可称之为准调相位。
2.2 系统控制模型及转子自动平衡方法分析
基于系统力学模型的理论推导和分析知道,电磁力与磁极线圈电流及转子振动响应均存在线性关系,依此可建立磁极线圈电流与转子振动响应之间的对应关系如下:

式中的h为转子振动响应z与磁极线圈电流i之间的线性映射关系。由于转子不平衡激振力消除的直接表现为相应振动的消除,因此如何寻求与转子最小振动响应对应的磁极线圈电流成为系统控制的核心问题。因此该系统在本质上可归结为以转子振动响应的最小幅值为寻优目标,磁极线圈电流的幅值和相位为寻优参数的寻优控制问题。建立控制模型的寻优目标函数如下:

Ai,φi分别为电流幅值和相位,z为振幅。
在明确寻优参数和性能指标的前提下,如何进行参数寻优是控制系统实施的核心问题。参考文献[9]的分步控制法,本研究对磁极线圈电流的控制分为两个过程:电流定幅值寻相位过程和定相位寻幅值过程。在振动平衡控制技术中,相位平衡过程最为复杂和重要,某种程度上相位的找准是决定控制效果的关键因素。以下主要进行定幅值寻相位控制过程的设计和分析。
根据上述分析设计定幅值整周搜索相位策略,以电流相位φi作为寻优参数,残余振动幅值z的平方最小为寻优指标,电流相位的变换次数为约束条件,建立单参数带约束寻优目标函数,

其中n为搜寻次数,Δφ为相位搜寻步长。

结合前面对作用力相位区域的分析可知,显然定幅值整周搜索相位算法的相位搜索空间包括了N区和P区,则控制过程中必然存在振动加剧过程。如果初始控制相位位于P区,对整周寻优模型进行改进如下所示:其中ΔφP=2π-2β*,即当作为寻优参数的电流相位φi的初值位于P区时,并保证整个搜索控制过程在P区完成,则理论上可实现转子振动无加剧自动平衡。磁极线圈控制电流的相位初值可通过振动相位与系统滞后角相结合的方法确定。
2.3 控制系统的建立
通常情况下,系统不平衡激振力的相位无法直接测取,而振动响应的相位是可以直接获得的,显然系统滞后角是求解平衡相位的关键。滞后角包括系统机械滞后角和测控系统滞后角,由于测控导致的滞后通常很小,可以忽略。因为系统结构及装配尺寸容易获得,考虑采用有限元转子动力学分析软件构建系统模型,对工作转速下系统模型进行辨识的方法获取所需系统滞后角,当控制系统工作时可以直接调用已获取的滞后角参数。该方案将大大缩短系统计算工作量,并加快控制系统的开发速度。
根据以上分析建立控制系统,如图3所示:

图3 控制系统示意图Fig.3 Control system diagram
为表述清楚,对系统图3中各个环节的输入输出量进行描述如下:

上面各式中的A为幅值,φ为相位。另外图中的zi为测控系统提取的振动信号,φ为工作转速下的系统机械滞后角(由有限元软件分析获得)。
该系统以磁极线圈电流为输入,转子作为控制对象,转子振动作为输出。转子在稳定运转状态下,不平衡激振力引起的振动视作扰动,其响应为zd;电磁控制力作用于转子系统产生的补偿振动为zc;系统最终振动视为残余振动e=zd+zc;振动控制器依据系统残余振动向转子提供所需的控制电流i;电磁力执行单元根据控制信号产生所需电磁力Fc,至此构成闭环控制结构。
3 实验台及系统动力学仿真
3.1 实验台介绍
为验证控制算法的可行性及有效性,以石化工业中离心压缩机为背景,搭建如图4所示实验台,模拟压缩机实际运转中叶轮不平衡故障。在实验台上,转子由20 kw电主轴直接驱动,转轴长876 mm,左右由两个可倾瓦轴承做支承形成单跨转子轴承系统,轴承跨距是490 mm,转轴直径为50 mm;为模拟压缩机中叶轮,在轴承跨内如图安装一个直径270 mm、厚度25 mm的飞轮,飞轮上圆周均布有16个M 8的螺纹孔,通过螺纹孔安装所需质量块来模拟转子在运行过程中的不平衡量。在连轴器上加工一个键槽,通过键相传感器检测转子旋转速度,同时也作为控制系统0相位标志。实验台中电磁平衡装置安装在飞轮旁边,如图所示安装位置,两者尽可能接近,以便能够模拟单平面转子。在电磁装置上安装电涡流振动位移传感器,用来测量转子振动,在可倾瓦轴承处也装有位移传感器,并通过OR38动态信号分析仪监测平衡效果。

图4 实验台实物图Fig.4 Experiment device
3.2 实验转子-轴承系统动力学仿真
为了获取转子轴承系统机械滞后角,利用转子动力学有限元分析软件DyRoBes_Rotor,建立了如图5所示的实验台有限元模型。

图5 转子实验装置有限元模型Fig.5 Finite element model of rotor experiment device
模型中可倾瓦轴承的刚度和阻尼系数用DyRoBes_Beperf软件分析,轴瓦结构参数及轴承刚度和阻尼系数如图6所示。

在电磁转子上施加1 000 g·mm的不平衡量进行不平衡响应的计算。此时右侧轴承(13号节点)处的不平衡响应如图7所示。图中的Probe1(x)所指曲线代表水平向测振处转子不平衡振动响应曲线;Probe2(y)所指曲线代表竖直向测振处的振动响应曲线。从图7的分析结果可知,该实验装置一阶临界转速为6 600 r/min。在2 100 r/min和3 000 r/min时,13号节点不平衡响应的相位分别为68.37°和81.89°。该角度即为右轴承处的振动相位相对于控制力的相位的滞后角。
在本文的控制算法中,将实际测得的振动相位减去滞后角再加180°即为所需要施加的控制力的相位。当然计算得到的滞后角会因为建模时的简化及轴承参数、供油温度的不确定性而有所偏差。但是按照这种方法计算得到的控制力相位使得第一次试探力就处在“P”区,使得控制效率更好,且在整个控制过程中不会出现振动加剧的情况。
4 实验结果及分析
在前面系统分析的指导下完成了控制程序的设计,为了验证实际控制系统的工作效果,在实验台上进行了不同转速下的实验,并通过OR38动态信号分析仪监测转子系统运转情况,控制效果如图8和9所示。
以图8中2 100 r/min下转子振动无加剧控制过程为例进行分析:阶段①为系统未加控制时初始振动状态;阶段②为在有限元分析获得的系统理论滞后角的指导下,结合系统在线测量辨识获得的振动相位求得系统平衡相位后,在P区进行定幅值寻相位的控制过程;阶段③为系统在求得平衡相位的基础上,进行定相位寻幅值的控制过程;阶段④为在系统获取最佳幅值和相位控制参数后的控制状态。图9振动控制过程趋势分析与图8相似。通过2 100 r/min和3 000 r/min两个转速下转子的控制效果图不难发现,整个平衡控制过程没有振动加剧的出现,实现了转子的自动平衡控制,并且最终系统振动峰峰值都小于10 um,振动从最大值到最小稳定值所用时间都在4秒以内,达到所希望的效果,验证了算法的正确性。

5 结论
本文在理论分析的基础上,结合电磁作用力式平衡装置的特点建立控制系统,实现了转子不平衡振动控制,并且确保振动过程中转子振幅不大于原始故障振动幅值。对控制力作用相位进行区域划分;利用有限元软件对转子系统进行工作转速下系统仿真分析,获取所需理论滞后角;在此基础上设计了定幅值寻相位的控制算法。为了实验的完整性,在相位寻优结束后,采用等步长搜索算法进行了定相位寻幅值过程,最后通过实验台在不同工作转速下对算法进行了有效性验证工作,并得到相关实验结果。实验结果表明本研究所提出的算法可以实现振动无加剧控制,实验过程与理论分析吻合。
由于本实验目前研究重点关注平衡相位的控制过程,下一步将考虑在平衡控制相位找准的基础上进行定相位寻幅值的控制研究,以期提高幅值的寻优精度和效率。
[1]王欲欣,杨东波,刘永光.旋转机械转子自动平衡实验研究[J].汽轮机技术,2000,42(4):225 -228.
[2] Gao Jinji,Wang Weimin,He Lidong.Fault Damage Power and Self-recovery System of Machinery[J].Key Engineering Materials Vols.413-414,2009:3-14.
[3]何立东,沈 伟,高金吉.转子在线自动平衡及其工程应用研究的进展[J].力学进展,2006,36(4):553-563.
[4]王维民,高金吉,江志农.基于有限元模型的旋转机械故障诊断方法研究[J].振动与冲击,2006,25(4):30-33.
[5]卢奂采.转子振动主动控制与轴向力在线动态监测研究[D].杭州:浙江大学,1996.
[6]朱美玲,汪凤泉.电磁式作动器及其振动主动控制系统的研究[J].振动.测试与诊断,1995,15(1):52-56.
[7]宣丽娟,王洪滨.具时滞的Jeffcott转子—电磁轴承系统的反馈控制设计[J].哈尔滨工业大学学报,2007,39(11):1833-1836.
[8]胡业发,周祖德,江征风.磁力轴承的基础理论与应用[M].北京:机械工业出版社,2006.
[9]陶利民.转子高精度动平衡测试与自动平衡技术研[D].长沙:国防科学技术大学,2006.
Optimal control method and test for rigid rotor auto-balancing
HUANG Li-quan,WANG Wei-min,SU Yi-ru,LI Yan,GAO Jin-ji
(Diagnosis and Self-recovery Research Center,Beijing University of Chemical Technology,Beijing 100029,China)
It is very important to eliminate online vibration of a rotor system in order to ensure reliable and efficient rotating machinery operation.In early period of rotor vibration control,a tentative control force is needed.The force may make the system vibration rise or drop,which depends on the relationship between the control force phase and the excitation force phase. Here, based on the rotor system dynamic analysis and controllable characteristics of electromagnetic force,the regional division of the control force phase was done.And the control model was built and some specific optimization strategy was proposed.The finite element analysis method was used to gain the system theoretic lagging angle under working speed.The phase of the control force was determined and this phase was used as the initial value of the optimal parameter to ensure the vibration amplitude being not larger than the initial fault amplitude of the rotor during control.Finally,the test table was established and the test results showed that the proposed method is effective.
electromagnetic force; automatic balance; self-recovery regulation; finite elementanalysis;optimal control
TH133;TP273
A
国家自然科学基金项目(50635010,50975018)
2009-12-24 修改稿收到日期:2010-03-11
黄立权 男,博士,1979年生
高金吉 男,院士,教授,1942年生

